
Originally I wasn’t planning to play any CTF during this weekend but Diamondroxxx asked me if I could as he and the other members of Social Engineering Experts were participating in Yauza CTF 2021, a Soviet themed CTF. Me and Diamondroxxx solved all the crypto challenges in Yauza in a few hours so we decided to check out Fword CTF after that (writeups for that can be found here).
We joined late for Yauza as it was Fri, 27 Aug. 2021, 20:00 SGT — Sun, 29 Aug. 2021, 20:00 SGT while we started playing at 9 am Saturday. In the end, we ranked 9th out of 227 scoring teams (and therefore qualifying for the finals), focusing only on the crypto challenges :
We managed to solve all 3 crypto challenges (the scoring system was generous to say the least) :
Below are the writeups :
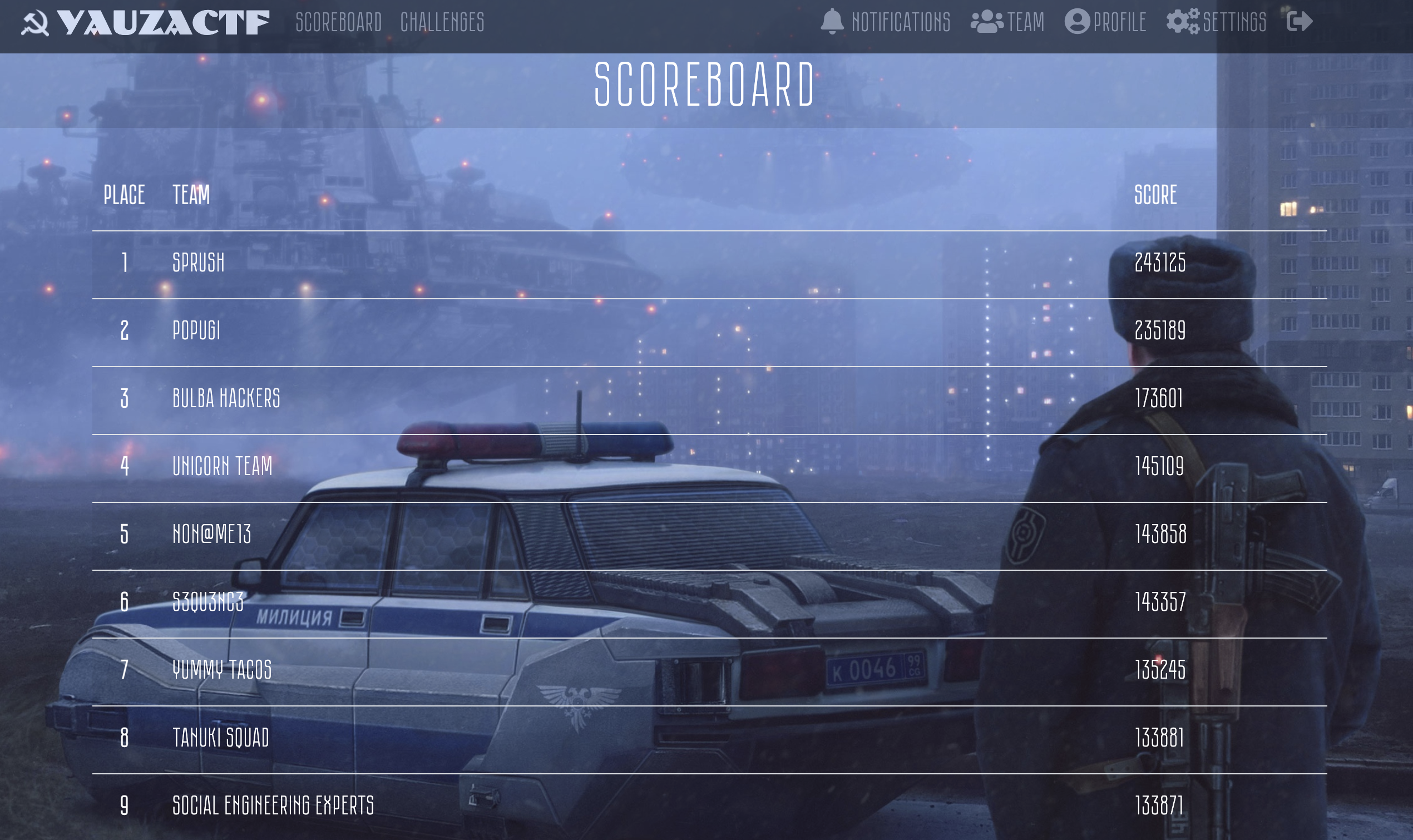
| Challenge | Category | Points | Solves |
|---|---|---|---|
| Signature | Crypto | 9109 | 31 |
| Knapsack | Crypto | 8856 | 35 |
| Sharing Secrets | Crypto | 7624 | 50 |
Signature
The server source code provided :
from Crypto.Hash import SHA256
from Crypto.Util.number import bytes_to_long, long_to_bytes, size, getRandomNBitInteger
from storage import flag
def byten(x, n):
return (x >> (n * 8)) & 0xFF
def mask(n):
return (1 << n) - 1
def rotate(x, n, s):
return ((x >> (s - n)) | (x << n)) & mask(s)
def scramble(x):
magic = 0xC3A569C3A569C3A569C3A569C3A569C33C965A3C965A3C965A3C965A3C965A3C
for i in range(32):
x = rotate(x, 27, 256) ^ rotate(magic, i, 256)
return x
def sha2(x):
hash = SHA256.new()
hash.update(x)
return hash.digest()
def gen_pair():
private = [getRandomNBitInteger(256) for _ in range(16)]
public = [long_to_bytes(y) for y in private]
for i in range(16):
for j in range(255):
public[i] = sha2(public[i])
return private, [bytes_to_long(y) for y in public]
def sign(x, key):
parts = [byten(x, i) for i in range(16)]
digest = [long_to_bytes(y) for y in key]
for i in range(16):
for j in range(parts[i]):
digest[i] = sha2(digest[i])
return digest
def verify(x, sign, public):
parts = [255 - byten(x, i) for i in range(16)]
digest = list(sign)
for i in range(16):
for j in range(parts[i]):
digest[i] = sha2(digest[i])
if digest[i] != long_to_bytes(public[i]):
return False
return True
def do_signature(x, private):
signature = sign(scramble(x), private)
return bytes_to_long(b''.join(signature))
def do_verify(x, signature, public):
signature = long_to_bytes(signature, 256*16//8)
signature = [signature[i*32:(i + 1)*32] for i in range(16)]
return verify(scramble(x), signature, public)
menu = '''\
[1] Sign message
[2] Get flag
[3] Quit'''
if __name__ == '__main__':
private, public = gen_pair()
challenge = getRandomNBitInteger(256)
while True:
try:
print(menu)
opt = input('> ')
if opt == '1':
data = int(input('msg: '))
if size(data) > 256:
raise Exception('Message is too long (256 bits max)')
if data == challenge:
raise Exception('Nice try')
print(do_signature(data, private))
elif opt == '2':
print('Enter signature for the message:')
print(challenge)
data = int(input('sign: '))
if size(data) > 256*16:
raise Exception('Signature is too long (16 blocks, 256 bits each)')
if not do_verify(challenge, data, public):
raise Exception('Wrong signature')
print(flag)
elif opt == '3':
exit(0)
else:
raise Exception('Unknown option')
except Exception as ex:
print('Error:', ex)
When we connect to the server, a public and private key pair is generated. Choosing option 1 allows us to input a message (as long as the message isn’t the same as the challenge - a random secret 256 bit number) after which a signature is calculated using do_signature and then returned to us. Option 2 prints the challenge and then asks us to provide a valid signature for that challenge. If you look carefully at the sign function which is called by do_signature. Before sign is called, a scramble operation is performed on the inputted message.. The vulnerability lies in the line parts = [255 - byten(x, i) for i in range(16)] as if for some reason parts is a list of 16 zeroes, the 2 for loops never run and instead the private key bytes are returned as digest = [long_to_bytes(y) for y in key] is returned where key is the private key (note that the private key is a list of 16 random 256 bit integers).
If we pass an input into option 1 which makes parts a list of zeroes, we obtain the signature which are just the private key bytes. With that, we can sign any message. So how to get parts equal zero? If we invert the scramble function to find the value which when scrambled gives 0. Inverting scramble is possible as we just need to flip the direction of the bitshifts for the functions scramble and rotate. After that, we can input that number which when scrambled gives 0 into the do_signature function to make parts a list of zeroes and hence obtain the private key bytes. With that we can sign the challenge and get the flag.
The solve script :
from pwn import *
from Crypto.Util.number import bytes_to_long, long_to_bytes
from Crypto.Hash import SHA256
local = False
debug = False
if local:
r = process(["python3", "test.py"], level='debug') if debug else process(["python3", "server.py"])
else:
r = remote("tasks.yauzactf.com", 30011, level = 'debug') if debug else remote("tasks.yauzactf.com", 30011)
def getChallenge():
r.sendlineafter("> ", b"2")
r.recvline()
challenge = r.recvline()
r.sendlineafter('sign: ', b"1001")
return int(challenge.decode())
def signMessage(m):
r.sendlineafter("> ", b"1")
r.sendlineafter('msg: ', str(m).encode())
signature = r.recvline()
return signature
def checkSignature(s):
r.sendlineafter("> ", b"2")
r.sendlineafter('sign: ', str(s).encode())
return r.recvline()
challenge = getChallenge()
def sha2(x):
hash = SHA256.new()
hash.update(x)
return hash.digest()
def byten(x, n):
return (x >> (n * 8)) & 0xFF
def mask(n):
return (1 << n) - 1
def rotate(x, n, s):
return ((x >> (s - n)) | (x << n)) & mask(s)
def invRotate(x, n, s):
return ((x << (s - n)) | (x >> n)) & mask(s)
def scramble(x):
magic = 0xC3A569C3A569C3A569C3A569C3A569C33C965A3C965A3C965A3C965A3C965A3C
for i in range(32):
x = rotate(x, 27, 256) ^ rotate(magic, i, 256)
return x
def invScramble(x):
magic = 0xC3A569C3A569C3A569C3A569C3A569C33C965A3C965A3C965A3C965A3C965A3C
for i in range(31, -1, -1):
x = invRotate(x ^ rotate(magic, i, 256), 27, 256)
return x
privateKeyBytes = long_to_bytes(signMessage(invScramble(0)))
privateKey = []
for i in range(0, len(privateKeyBytes), 32):
privateKey.append(bytes_to_long(privateKeyBytes[i:i+32]))
print(challenge)
print(privateKey)
def sign(x, key):
parts = [byten(x, i) for i in range(16)]
digest = [long_to_bytes(y) for y in key]
for i in range(16):
for j in range(parts[i]):
digest[i] = sha2(digest[i])
return digest
def do_signature(x, private):
signature = sign(scramble(x), private)
return bytes_to_long(b''.join(signature))
def verify(x, sign, public):
parts = [255 - byten(x, i) for i in range(16)]
digest = list(sign)
for i in range(16):
for j in range(parts[i]):
digest[i] = sha2(digest[i])
if digest[i] != long_to_bytes(public[i]):
return False
return True
def do_verify(x, signature, public):
signature = long_to_bytes(signature, 256*16//8)
signature = [signature[i*32:(i + 1)*32] for i in range(16)]
return verify(scramble(x), signature, public)
public = [long_to_bytes(y) for y in privateKey]
for i in range(16):
for j in range(255):
public[i] = sha2(public[i])
public = [bytes_to_long(y) for y in public]
forgedSignature = do_signature(challenge, privateKey)
assert do_verify(challenge, forgedSignature, public)
print(checkSignature(forgedSignature))
Flag : YauzaCTF{Crypt0_$1gn3rrrr}
Knapsack
The flag.txt and pubkey.txt files can be found here and here. The challenge name suggests that the flag was encrypted using the Merkle–Hellman knapsack cryptosystem. I hadn’t heard of this before but one repositry which contains a huge list of common crypto attacks did have one for this system, something known as a Low Density Attack. That can be found here. So we just used that to get the flag. We don’t know anything about lattices :(
The Sage solve script :
from math import ceil
from math import log2
from math import sqrt
from sage.all import matrix
from sage.all import QQ
from Crypto.Util.number import long_to_bytes
def attack(a, s):
"""
Tries to find e_i values such that sum(e_i * a_i) = s.
This attack only works if the density of the a_i values is < 0.9048.
More information: Coster M. J. et al., "Improved low-density subset sum algorithms"
:param a: the a_i values
:param s: the s value
:return: the e_i values, or None if the e_i values were not found
"""
n = len(a)
d = n / log2(max(a))
N = ceil(sqrt(1 / 2 * n))
assert d < 0.9408, f"Density should be less than 0.9408 but was {d}."
M = matrix(QQ, n + 1, n + 1)
for i in range(n):
M[i, i] = 1
M[i, n] = N * a[i]
M[n] = [1 / 2] * n + [N * s]
L = M.LLL()
for row in L.rows():
s_ = 0
e = []
for i in range(n):
ei = 1 - (row[i] + 1 / 2)
if ei != 0 and ei != 1:
break
ei = int(ei)
s_ += ei * a[i]
e.append((str(ei)))
if s_ == s:
#print(e)
return e
pubkey = [2948549611747, 2043155587142, 361533419625, 1001380428657, 2438250374319, 1059738568330, 115120002311, 198226659880, 2343897184958, 2592576935132, 2327834076450, 237536244289, 309228208827, 3327276767693, 462372704541, 2176574227058]
flag = [12777998288638, 10593582832873, 7834439533378, 10486500991495, 14714582460036, 7568907598905, 12800035735033, 14724457772647, 11910445040159, 11202963622894, 10291238568620, 15103559399914, 13156142631772, 16988824411176]
actualFlag = ""
for i in flag:
actualFlag += ''.join(attack(pubkey, i))
print(long_to_bytes(int(actualFlag, 2)))
Flag : YauzaCTF{l34ky_kn4ps4k_d4mn}
Sharing Secrets
The source code provided :
import json
from Crypto.Util.number import bytes_to_long, getPrime
from storage import flag
def mul(x):
m = 1
for i in x:
m *= i
return m
if __name__ == '__main__':
flag = bytes_to_long(flag.encode())
count = 25
threshold = 11
psize = 24
primes = list(sorted(getPrime(psize) for _ in range(count)))
pmin = mul(primes[-threshold + 1:])
pmax = mul(primes[:threshold])
assert pmin < flag < pmax
shadows = [flag % x for x in primes]
with open('secrets.json', 'wt') as out_file:
out_file.write(json.dumps({
'shadows': shadows[1:threshold],
'primes': primes[:threshold],
'threshold': threshold
}))
The secrets.json file can be found here. Firstly, a list of 25 primes is generated. Afterwards, the last 10 primes are multiplied with each other and stored in pmin. The first 11 primes are multiplied with each and stored in pmax. Note that pmin < flag < pmax. Afterwards, so called ‘shadows’ are calculated by flag % x where x is from the list of primes. Since the flag is obviously bigger than any prime, this means that we have values which have ‘wrapped’ around the modulus (the prime) multiple times.
The first 11 primes are provided to us along with 10 corresponding primes (the first prime’s shadow isn’t provided). We could use the Chinese Remainder Theorem to solve the challenge. In number theory, the Chinese remainder theorem (CRT) states that if one knows the remainders of the Euclidean division of an integer n by several integers, then one can determine uniquely the remainder of the division of n by the product of these integers, under the condition that the divisors are pairwise coprime.
In our case, the dividend n is the flag itself, 10/11 of the remainders are known as they are the shadows while it is worth noting that the divisors are all prime and are hence coprime to each other. We can first get the CRT of the 10 known shadows with the 11 primes. To get the flag, we still don’t know the first shadow (the first remainder) so we can keep adding multiples of the last 10 primes multiplied by each other (denoted by lcm) to the original CRT until we get the flag (we can check this by verifying if the resulting integer contains the flag format).
Our Sage solve script :
shadows = [7832917, 8395798, 4599919, 154544, 3430534, 4694683, 123690, 5911445, 7380167, 10597668]
primes = [8412883, 8889941, 9251479, 9471269, 9503671, 9723401, 10092149, 10389901, 10551241, 10665527, 11099951]
def mul(x):
m = 1
for i in x:
m *= i
return m
lcm = mul(primes[1:])
flag = CRT_list(shadows, primes[1:])
for i in range(primes[0]):
flag += lcm
flag_bytes = int(flag).to_bytes(40, "big")
if b"Yauza" in flag_bytes:
print(flag_bytes)
exit()
Flag : YauzaCTF{k33p_1t_1n_7h3_sh4d0w5}