
Originally I wasn’t planning to play any CTF during this weekend but Diamondroxxx asked me if I could as he and the other members of Social Engineering Experts were participating in Yauza CTF 2021, a Soviet themed CTF. Me and Diamondroxxx solved all the crypto challenges in Yauza in a few hours so we decided to check if there was some CTF going on.
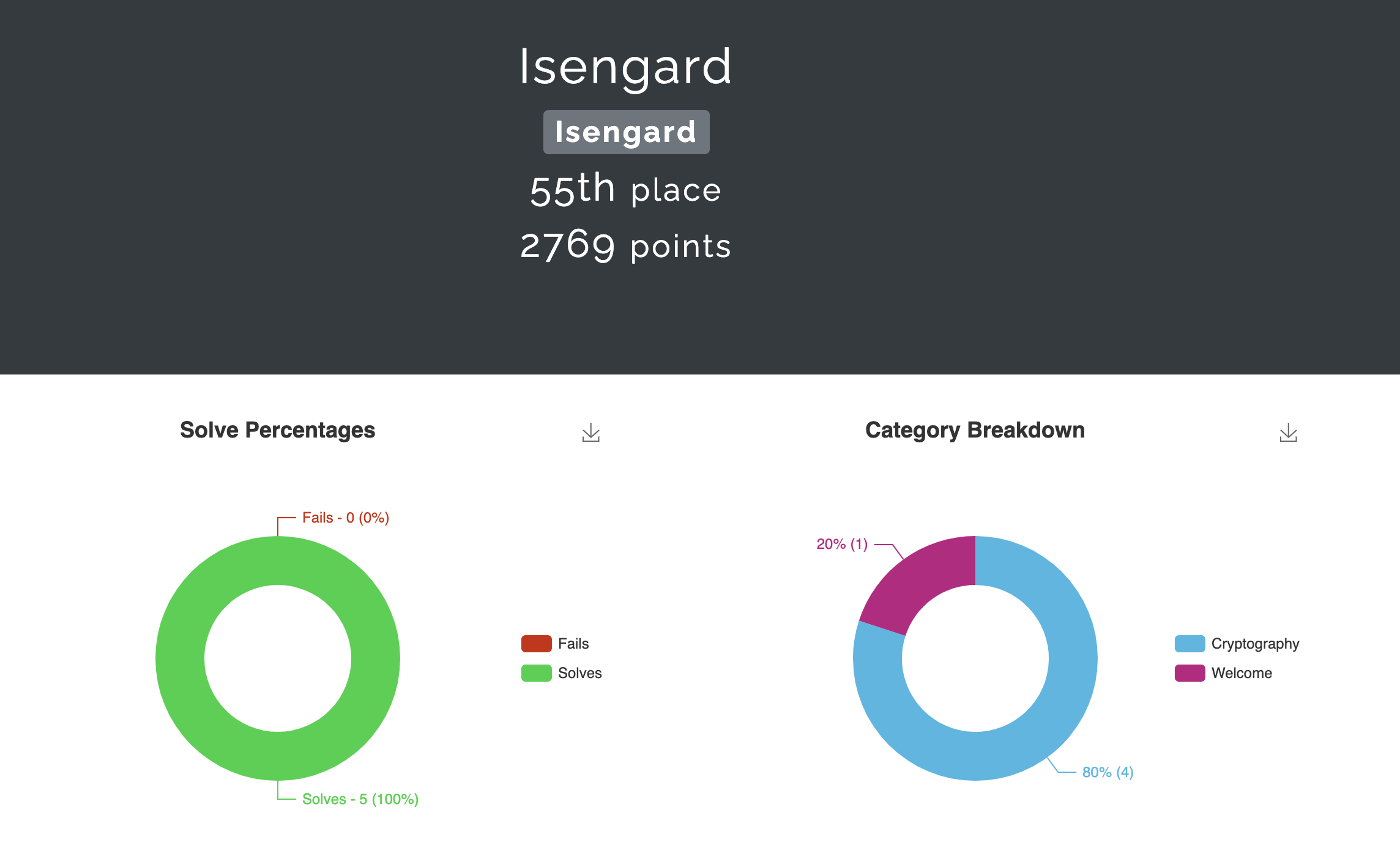
Turns out Fword, the top CTF team from Tunisia, was hosting their own Fword CTF 2021 and it had some crypto challenges so we decided to play as Isengard as it was only the both of us for that. Sadly we joined late for both CTFs. Fword was only 1 and a half days long and was from Sat, 28 Aug. 2021, 01:00 SGT — Sun, 29 Aug. 2021, 13:00 SGT and we only joined at around 4pm on Saturday. We tried to solve as many crypto challenges as we could until 3 am (we were stuck on the Ed25519 curve challenge). We ranked 55th out of 428 scoring teams, focusing only on the crypto challenges.
Solved challenges stats :
Timestamps of the challenges we solved :
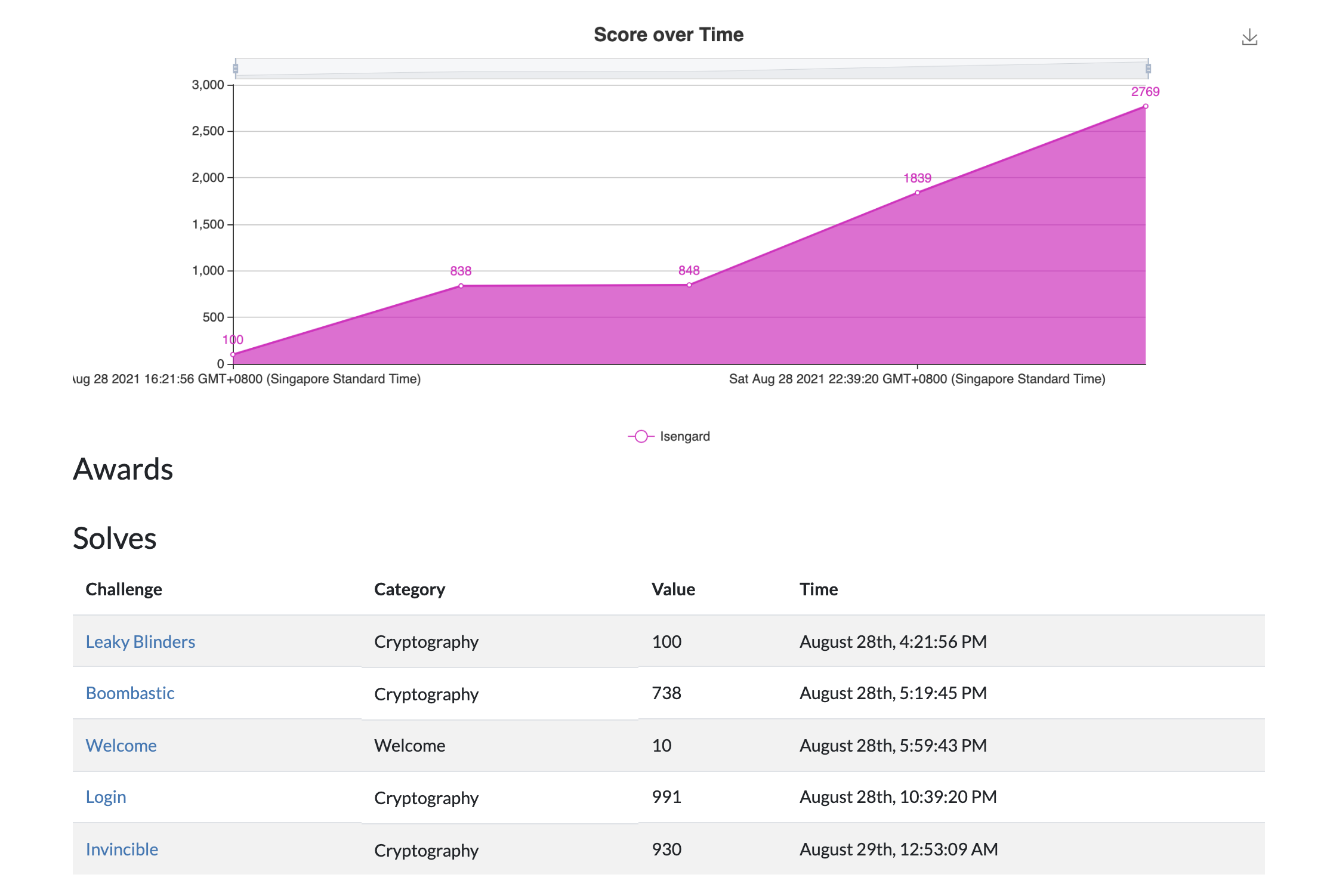
We managed to solve 4 out of the 6 crypto challenges :

Below are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
| Login | Crypto | 991 | 11 |
| Invincible | Crypto | 930 | 29 |
| Boombastic | Crypto | 738 | 55 |
| Leaky Blinders | Crypto | 100 | 121 |
| Welcome | Welcome | 10 | 369 |
Login
The server source code provided :
#!/usr/bin/env python3.8
from Crypto.Util.number import bytes_to_long, long_to_bytes, inverse, getPrime, GCD
import os, hashlib, sys, signal
from time import time
FLAG = "FwordCTF{####################################################################}"
WELCOME = '''
Welcome to CTFCreators Website.
We are a challenges development startup from a team of cybersecurity professionals with diverse backgrounds and skills.'''
server_token = os.urandom(16)
message_to_sign = b"https://twitter.com/CTFCreators"
def H(msg):
return hashlib.sha256(msg).digest()
def gen_key():
while True:
p, q = getPrime(1024), getPrime(1024)
N = p * q
e = 65537
phi = (p - 1) * (q - 1)
if GCD(e, phi) == 1:
break
d = inverse(e, phi)
pinv = inverse(p, q)
return N, e, d, pinv
def verify(signature, e, N):
try:
signature = int(signature, 16)
msg = bytes_to_long(message_to_sign)
verified = pow(signature, e, N)
if (verified == msg):
return True
else:
return False
except:
return False
def sign_up():
user = str(input("\nUsername : ")).encode()
proof = b'is_admin=false'
passwd = H(server_token + b';' + user + b';' + proof)
return user.hex(), proof.hex(), passwd.hex()
def log_in(username, proof, password):
if password == H(server_token + b';' + username + b';' + proof):
if b'is_admin=true' in proof:
return True
return False
class Login:
def __init__(self):
print(WELCOME)
def start(self):
try:
while True:
print("\n1- Sign up")
print("2- Login")
print("3- Leave")
c = input("> ")
if c == '1':
usr, prf, pwd = sign_up()
print(f"\nAccount created.\nUsername : {usr}\nPassword : {pwd}\nProof : {prf}")
elif c == '2':
user = bytes.fromhex(input("\nUsername : "))
passwd = bytes.fromhex(input("Password : "))
proof = bytes.fromhex(input("Proof : "))
if log_in(user, proof, passwd):
N, e, d, pinv = gen_key()
print(f"Welcome admin, to continue you need to sign this message : '{message_to_sign}'")
print(f"e : {hex(e)}")
print(f"d : {hex(d)}")
print(f"inverse(p, q) : {hex(pinv)}")
sig = input("Enter your signature : ")
if verify(sig, e, N):
print(f"Long time no see. Here is your flag : {FLAG}")
else:
sys.exit("Disconnect.")
else:
sys.exit("Username or password is incorrect.")
elif c == '3':
sys.exit("Goodbye :)")
except Exception as e:
print(e)
sys.exit("System error.")
signal.alarm(60)
if __name__ == "__main__":
challenge = Login()
challenge.start()
While one may be tempted to straight away think that the main goal of the challenge is to somehow create a valid signature where the cryptosystem used is some form of RSA, you first have to login (hence the challenge name). Choosing option 1 allows you to enter a username. After that using the function sign_up(), a password P is generated which is a SHA-256 hash (H) of a server token st (16 random and unknown secret bytes) followed by the entered username and then a proof set to is_admin=false such that :
Password = H(st + user + proof)
After an ‘account’ is created, the password (the hash), entered username and current proof is provided to us. Now if we want to login using option 2, we are prompted to enter a username, a password and proof. This is then checked using the function log_in. Over here we have to ensure that the password that we provided (a SHA-256 hash) matches the hash of the 16 unknown server token bytes along with the provided username and a proof set to is_admin=true. Obviously the hash that we got from option 1 is incorrect because the proof had admin set to false not true. Since we don’t know the 16 secret server token bytes, we cannot compute a hash ourselves and obviously it is impossible to reverse SHA-256. Eventually after some reading, we came across something known as a Hash Length Extension Attack.
In a hash length extension attack, if one knows the hash (H) of a message appended to some secret key, so known = H(sk + m), where only the message and the length of the secret key is known, one can calculate the hash of the secret key followed by the known message with some padding followed by a desired final message. Hence we can compute a valid hash for logging in without ever knowing the 16 secret server token bytes such that :
Entered Password = H(st + user + padding (length extension) + proof)
where the username we input in option 2 is user+padding and the proof is set to is_admin=true. We used this Python hash extender in order to calculate the extension. After logging in, we are then given some of the parameters of the RSA cryptosystem - the public exponent (e) and curiously the private key (d) along with the result of the modular multiplicative inverse of the prime p with respect to q. Most notably, we are not given the public modulus N.
Our goal is to generate a valid signature for the message https://twitter.com/CTFCreators where our signature is validated by the server using the verify method. Looking at the verification function, we can clearly see from the line verified = pow(signature, e, N) that verification is analogous to the encryption of a message in RSA as ciphertext = pow(m, e, N). So our signature should be the same as the decryption of a message for RSA so signature = pow(m, d, N). Note that this is how signatures are generated using RSA and the vulnerability is obviously that the private key d is provided to us.
It still isn’t straightforward to generate the signature as we don’t have the modulus N yet. Somehow, using the private key, public exponent and the modular inverse of p with respect to q, we had to derive N after which we can sign the message and get the flag. After some reading, we realized that this writeup contained the solution, the explanation being summarised below :
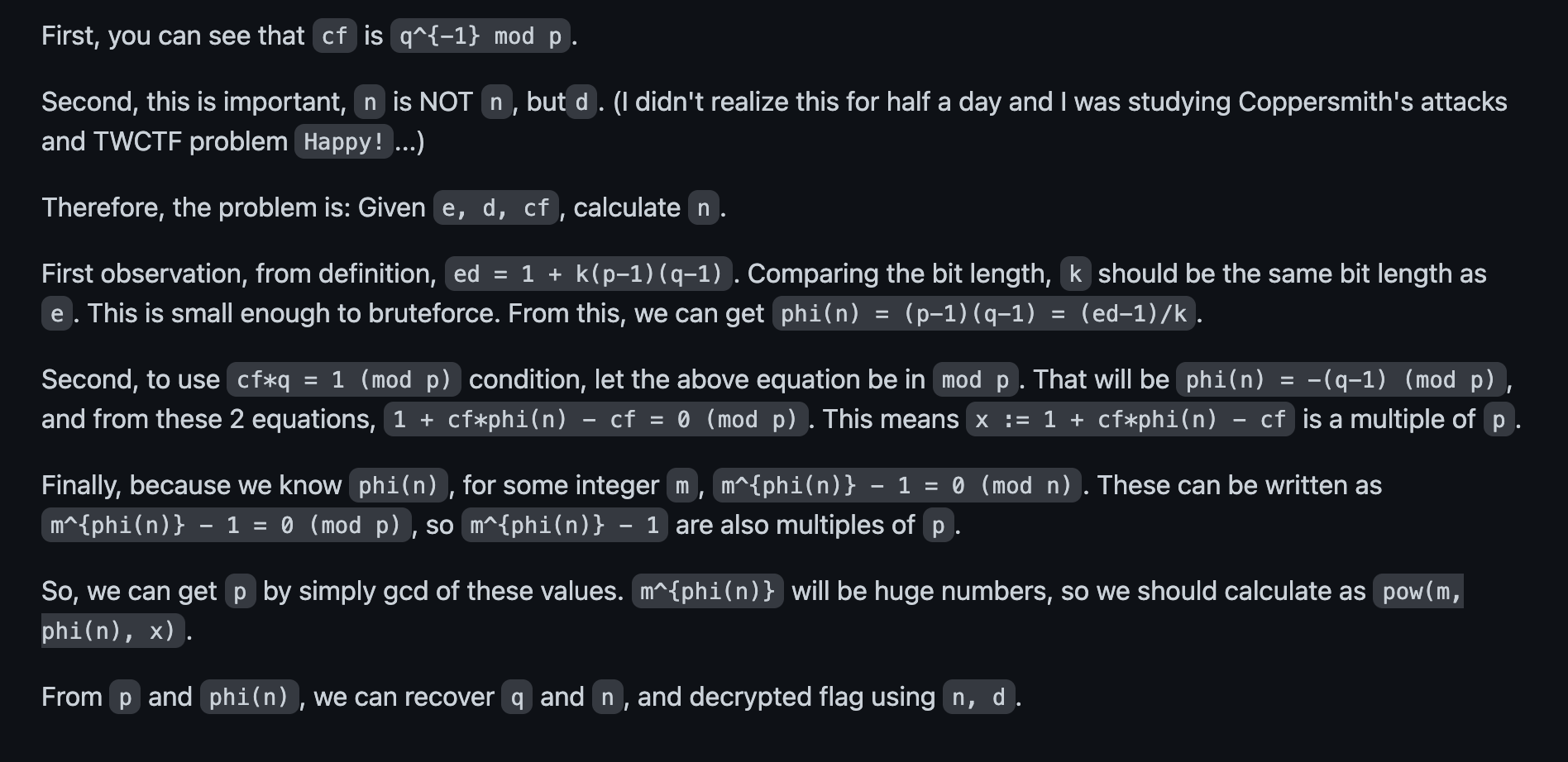
One thing to note is that in the writeup, the range of possible k values where (ed-1)*e / k == (p-1)*(q-1) traversed was from 1 to 100,000 but in reality, the possible values of k would not exceed the public exponent e = 65537.
Our solve script :
from pwn import *
from Crypto.Util.number import bytes_to_long, long_to_bytes, inverse, getPrime, GCD
import os, hashlib, sys, signal
#https://github.com/stephenbradshaw/hlextend
import hlextend
from math import gcd
from sympy import isprime
local = False
debug = True
if local:
r = process(["python3", "local.py"], level='debug') if debug else process(["python3", "local.py"])
else:
r = remote("52.149.135.130", 4871, level = 'debug') if debug else remote("52.149.135.130", 4871)
r.sendlineafter('> ', b'1')
user = b'hi'
r.sendlineafter('Username : ', user)
r.recvuntil(b'Account created.\n')
username = r.recvline()[11:].decode().strip()
password = r.recvline()[11:].decode().strip()
proof = r.recvline()[8:].decode().strip()
sha = hlextend.new('sha256')
extension = sha.extend(';is_admin=true', ';hi;is_admin=false', 16, password)[1:-14]
r.sendlineafter('> ', b'2')
r.sendlineafter('Username : ', eval(f"b'{extension}'").hex())
passwdPayload = sha.hexdigest()
r.sendlineafter('Password : ', passwdPayload.encode())
proofPayload = b'is_admin=true'
r.sendlineafter('Proof : ', proofPayload.hex().encode())
print(r.recvline())
e = int(r.recvline()[4:].decode().strip(), 16)
d = int(r.recvline()[4:].decode().strip(), 16)
inversePQ = int(r.recvline()[16:].decode().strip(), 16)
upper_lim = min(e, d)
ks = []
for k in range(2, upper_lim):
if (e * d - 1) % k == 0 and ((e * d - 1) // k).bit_length() <= 2048:
ks.append(k)
# print("[*] Possible number of k values = ", len(ks)) # 1
print(f"List of possible Ks = {ks}")
#https://gist.github.com/n-ari/a2db9af7fd3c172e4fa65b923a66beff
for k in ks:
print(f"K checked is {k}")
phi = (e*d - 1) // k
c1 = (phi - 1) * inversePQ + 1
factors = [c1]
for i in range(2, 11):
factors.append(pow(i, phi, c1) - 1)
q = gcd(*factors)
if q.bit_length() != 1024 or not isprime(q): continue
print(f"q : {q} and isprime = {isprime(q)}")
p = phi // (q - 1) + 1
if d != inverse(e, (p-1)*(q-1)) or p.bit_length() != 1024 or not isprime(p): continue
print(f"p : {p} and isprime = {isprime(p)}")
if inversePQ != inverse(p, q) : continue
break
n = p*q
print(n)
message_to_sign = b"https://twitter.com/CTFCreators"
payload = hex(pow(bytes_to_long(message_to_sign), d, int(n)))[2:]
r.sendlineafter('Enter your signature : ', payload)
print(r.recvline())
And after running the script, we can see that the possible values of phi are selected and after reconstructing the modulus and hence the signature, we got the flag :
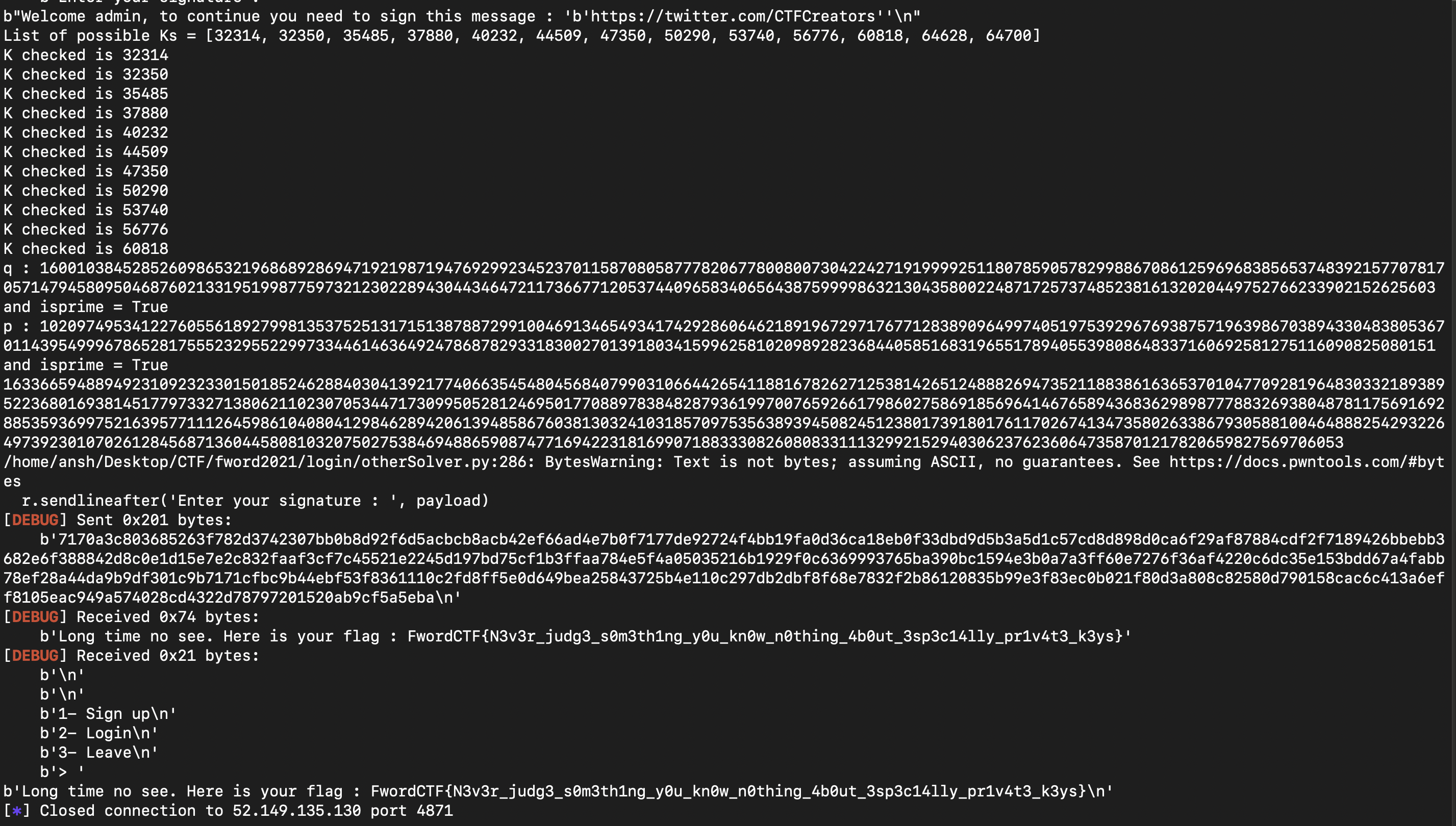
Flag : FwordCTF{N3v3r_judg3_s0m3th1ng_y0u_kn0w_n0thing_4b0ut_3sp3c14lly_pr1v4t3_k3ys}
Invincible
The server source code provided :
#!/usr/bin/env python3.8
from Crypto.Util.number import inverse
from Crypto.Cipher import AES
from collections import namedtuple
import random, sys, os, signal, hashlib
FLAG = "FwordCTF{#######################################################}"
WELCOME = '''
Welcome to my Invincible Game, let's play.
If you can decrypt all my messages that I will give, You win.
(( _______
_______ /\O O\
/O /\ / \ \
/ O /O \ / O \O____O\ ))
((/_____O/ \ \ /O /
\O O\ / \ / O /
\O O\ O/ \/_____O/
\O____O\/ ))
You get to choose your point first.
'''
Point = namedtuple("Point","x y")
class EllipticCurve:
INF = Point(0, 0)
def __init__(self, a, b, Gx, Gy, p):
self.a = a
self.b = b
self.p = p
self.G = Point(Gx, Gy)
def add(self, P, Q):
if P == self.INF:
return Q
elif Q == self.INF:
return P
if P.x == Q.x and P.y == (-Q.y % self.p):
return self.INF
if P != Q:
tmp = (Q.y - P.y)*inverse(Q.x - P.x, self.p) % self.p
else:
tmp = (3*P.x**2 + self.a)*inverse(2*P.y, self.p) % self.p
Rx = (tmp**2 - P.x - Q.x) % self.p
Ry = (tmp * (P.x - Rx) - P.y) % self.p
return Point(Rx, Ry)
def multiply(self, P, n):
R = self.INF
while 0 < n:
if n & 1 == 1:
R = self.add(R, P)
n, P = n >> 1, self.add(P, P)
return R
p = 0xffffffff00000001000000000000000000000000ffffffffffffffffffffffff
a = -0x3
Gx = 0x55b40a88dcabe88a40d62311c6b300e0ad4422e84de36f504b325b90c295ec1a
Gy = 0xf8efced5f6e6db8b59106fecc3d16ab5011c2f42b4f8100c77073d47a87299d8
b = 0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b
E = EllipticCurve(a, b, Gx, Gy, p)
class RNG:
def __init__(self, seed, P, Q):
self.seed = seed
self.P = P
self.Q = Q
def next(self):
s = E.multiply(self.P, self.seed).x
self.seed = s
r = E.multiply(self.Q, s).x
return r & ((1<<128) - 1)
def encrypt(msg, key, iv):
aes = AES.new(key, AES.MODE_CBC, iv)
cipher = aes.encrypt(msg)
return iv + cipher
def decrypt(cipher, key, iv):
aes = AES.new(key, AES.MODE_CBC, iv)
msg = aes.decrypt(cipher)
return msg
class Invincible:
def __init__(self):
print(WELCOME)
def start(self):
try:
Px = int(input("Point x : "))
Py = int(input("Point y : "))
P = Point(Px, Py)
if (P == E.INF) or (Px == 0) or (Py == 0):
print("Don't cheat.")
sys.exit()
print(f"Your point : ({P.x}, {P.y})")
Q = E.multiply(E.G, random.randrange(1, p-1))
print(f"\nMy point : ({Q.x}, {Q.y})")
rng = RNG(random.getrandbits(128), P, Q)
for _ in range(100):
key = hashlib.sha1(str(rng.next()).encode()).digest()[:16]
iv = os.urandom(16)
msg = os.urandom(64)
cipher = encrypt(msg, key, iv)
print(f"\nCiphertext : {cipher.hex()}")
your_dec = bytes.fromhex(input("What was the message ? : "))
if your_dec == msg:
print("Correct.")
else:
print("You lost.")
sys.exit()
print(f"Congratulations ! Here's your flag : {FLAG}")
except Exception:
print("System error.")
sys.exit()
signal.alarm(360)
if __name__ == "__main__":
challenge = Invincible()
challenge.start()
This challenge is based on ECC (Elliptic Curve cryptography). When we connect to the server, we are asked to enter a set of co-ordinates P (as long as either point is not equal to 0). After that, a point Q is generated by multipling the generator point G with some random number between 1 and a very large prime p. This is how ECC works, we start off a base (generator) point, multiply (point addition) it a secret number of times and end up at a final point Q. Trying to obtain the secret number of times the generator is multiplied by is equivalent to solving the discrete logarithm problem.
After that, a random number is generated using the RNG class where a random 128 bit number along with our chosen point P and the server generated point Q is inputted. THe random 128 bit number is the seed of the RNG (random number generator). A random number is generated by calling the next attribute of RNG. Inside next, an integer s is calculated by getting the x co-ordinate of multiplying our given point P with the seed. The seed is then set to s and after that, a value r is calculated by getting the x co-ordinate of Q muliplied by s. The first 128 bits of this number is then outputted as the ‘random’ number and the SHA-1 hash of this number is used as a key for AES CBC mode encryption.
The challenge is pretty evident. We have to pass 100 rounds where in each round, the aforementioned key is generated using the RNG and then a random 16 byte IV is created along with a random 64 byte message. This is then encrypted and the ciphertext along with IV is given to us. Somehow, we have to guess the original message and if it is correct, we pass the level and proceed to the next one and if are wrong, the server session ends. After passing all 100 levels, we get the flag.
So the trick is to predict the key somehow by exploiting a flaw in the RNG. After some reading, we came across this article which described an Invalid Curve attack. Basically, if we use some standard elliptic curve, a careful selection should give us a curve with a large set of points. These points form a group G with a generator point P (base point) with order n. The order defines the smallest number such that (n+1) * P = P. In other words, if we execute the ADD operation with the base point (n+1) times, we visit all the points on the curve and get back to the base point. Hene the number of possible values for a correctly chosen curve would be enormous!
However, in an invalid curve attack, we could force the server to use the point P such that P is a point outside the defined curve where the invalid point could belong to a different curve, which consists of a very small number of elements. In our case, Googling the given curve parameters shows that we have a secp256r1 (also known as prime256v1) curve (though the base point G differs). Curiously, this is the same curve as the one used in the article to highlight how given a set of invalid points outside this curve, we get only five possible results (four points and a point in infinity). After using the set of invlaid points given in the article and running it in this test script, we realized that there are probably only 3 possible values of s no matter what the seed is.
If we know the original value of s, we can predict the first state and hence all subsequent random numbers as the next ‘random number’ is based on the previous state. Hence, we could assume that the original state is one of the 3 numbers we found using the test script and subsequently get all states and hence keys. Using this, we would only have to run this a few times as we don’t know which of the 3 numbers is chosen first (eventually one of the 3 will be picked). Using this method, we first generated the 3 sets of key values where each set’s original state is each of the 3 numbers. After that, we ran a loop until we got the correctly chosen number (probability is high as it is has a chance of 1/3, running this a few times increases probability of choosing a correct value much more). Hence with the correct key and given IV, we could decrypt the ciphertext and hence obtain the message and this the flag.
Our solve script :
from Crypto.Util.number import inverse
from Crypto.Cipher import AES
from collections import namedtuple
import random, sys, os, signal, hashlib
from pwn import *
local = False
debug = False
if local:
r = process(["python3", "invincible.py"], level='debug') if debug else process(["python3", "invincible.py"])
else:
r = remote("52.149.135.130", 4874, level = 'debug') if debug else remote("52.149.135.130", 4874)
#==================Server Code==================
Point = namedtuple("Point","x y")
class EllipticCurve:
INF = Point(0, 0)
def __init__(self, a, b, Gx, Gy, p):
self.a = a
self.b = b
self.p = p
self.G = Point(Gx, Gy)
def add(self, P, Q):
if P == self.INF:
return Q
elif Q == self.INF:
return P
if P.x == Q.x and P.y == (-Q.y % self.p):
return self.INF
if P != Q:
tmp = (Q.y - P.y)*inverse(Q.x - P.x, self.p) % self.p
else:
tmp = (3*P.x**2 + self.a)*inverse(2*P.y, self.p) % self.p
Rx = (tmp**2 - P.x - Q.x) % self.p
Ry = (tmp * (P.x - Rx) - P.y) % self.p
return Point(Rx, Ry)
def multiply(self, P, n):
R = self.INF
while 0 < n:
if n & 1 == 1:
R = self.add(R, P)
n, P = n >> 1, self.add(P, P)
return R
p = 0xffffffff00000001000000000000000000000000ffffffffffffffffffffffff
a = -0x3
Gx = 0x55b40a88dcabe88a40d62311c6b300e0ad4422e84de36f504b325b90c295ec1a
Gy = 0xf8efced5f6e6db8b59106fecc3d16ab5011c2f42b4f8100c77073d47a87299d8
b = 0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b
E = EllipticCurve(a, b, Gx, Gy, p)
class RNG:
def __init__(self, seed, P, Q):
self.seed = seed
self.P = P
self.Q = Q
def next(self):
s = E.multiply(self.P, self.seed).x
self.seed = s
r = E.multiply(self.Q, s).x
return r & ((1<<128) - 1)
def encrypt(msg, key, iv):
aes = AES.new(key, AES.MODE_CBC, iv)
cipher = aes.encrypt(msg)
return iv + cipher
def decrypt(cipher, key, iv):
aes = AES.new(key, AES.MODE_CBC, iv)
msg = aes.decrypt(cipher)
return msg
#==================Solve Script==================
SVALS = [46111711714004764615393195350570532019484583409650937480110926637425134418118,
82794344854243450371984501721340198645022926339504713863786955730156937886079,
0]
Px = 82794344854243450371984501721340198645022926339504713863786955730156937886079
Py = 33552521881581467670836617859178523407344471948513881718969729275859461829010
P = Point(Px, Py)
# Our point
def sendP():
r.sendlineafter(b"Point x : ", str(Px).encode())
r.sendlineafter(b"Point y : ", str(Py).encode())
r.recvline()
sendP()
# Their point
def getQ():
r.recvuntil(b"(")
Qx, Qy = [int(n.decode()) for n in r.recvline(keepends=False)[:-1].split(b", ")]
Q = Point(Qx, Qy)
return Q
Q = getQ()
keyvals = [hashlib.sha1(str(E.multiply(Q, s).x & ((1<<128) - 1)).encode()).digest()[:16] for s in SVALS]
for i in range(10):
try:
key = keyvals[i % len(SVALS)]
for i in range(100):
r.recvuntil(b" : ")
cipher = bytes.fromhex(r.recvline(keepends=False).decode())
iv, ct = cipher[:16], cipher[16:]
msg = decrypt(ct, key, iv)
r.sendlineafter(b"What was the message ? : ", msg.hex().encode())
print(r.recvline())
print(r.recvline())
exit(0)
except EOFError:
if local:
r = process(["python3", "invincible.py"], level='debug') if debug else process(["python3", "invincible.py"])
else:
r = remote("52.149.135.130", 4874, level = 'debug') if debug else remote("52.149.135.130", 4874)
sendP()
Q = getQ()
keyvals = [hashlib.sha1(str(E.multiply(Q, s).x & ((1<<128) - 1)).encode()).digest()[:16] for s in SVALS]
And after running our script, we passed all 100 levels and got the flag :
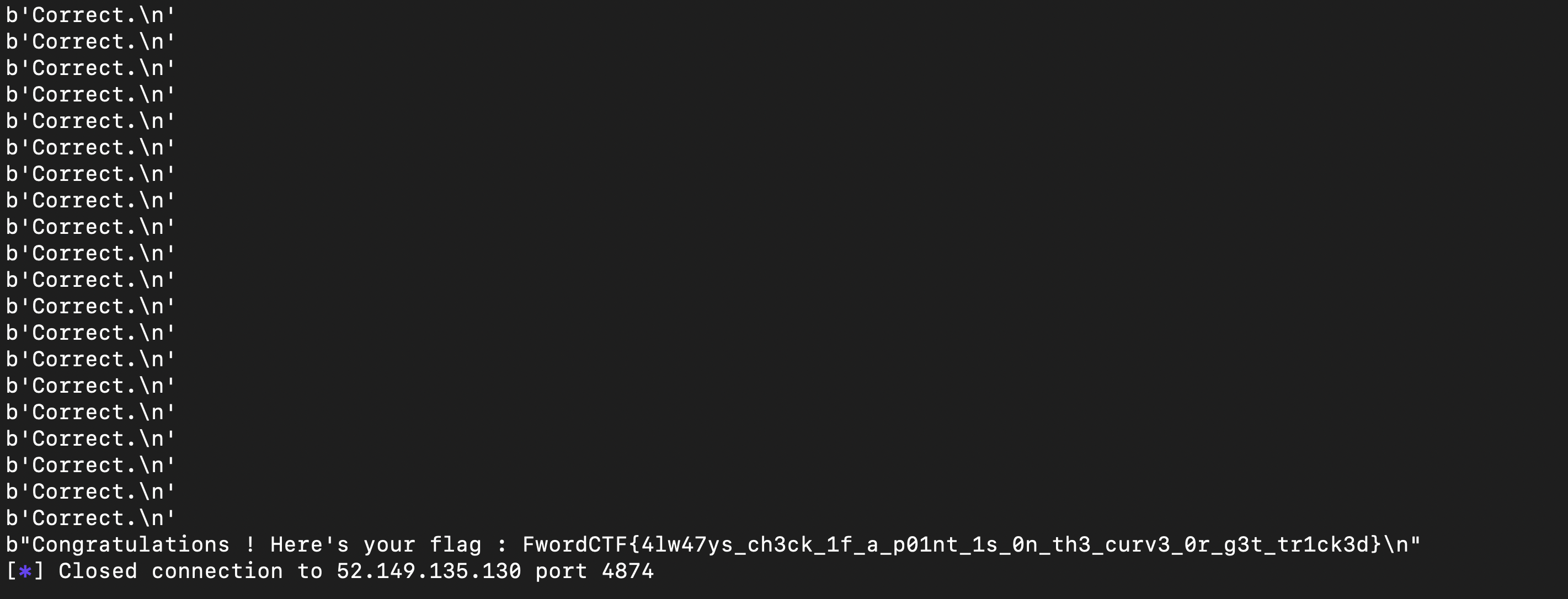
Flag : FwordCTF{4lw47ys_ch3ck_1f_a_p01nt_1s_0n_th3_curv3_0r_g3t_tr1ck3d}
Boombastic
The server source code provided :
#!/usr/bin/env python3.8
from Crypto.Util.number import getStrongPrime, inverse
from json import loads, dumps
import hashlib, sys, os, signal, random
FLAG = "FwordCTF{###############################}"
WELCOME = '''
______________
_(______________()
______ _- | ||
| |_ _- | ||
| |_|_ | Boombastic ||
|______| -_ | ||
/\\ -_|______________||
/ \\
/ \\
/ \\
'''
p = getStrongPrime(1024)
secret = random.randint(1, p-1)
def get_ticket(code):
y = int(hashlib.sha256(code.encode()).hexdigest(),16)
r = ((y**2 - 1) * (inverse(secret**2, p))) % p
s = ((1 + y) * (inverse(secret, p))) % p
return {'s': hex(s), 'r': hex(r), 'p': hex(p)}
class Boombastic:
def __init__(self):
print(WELCOME)
def start(self):
try:
while True:
print("\n1- Enter Cinema")
print("2- Get a ticket")
print("3- Leave")
c = input("> ")
if c == '1':
magic_word = loads(input("\nEnter the magic word : "))
if magic_word == get_ticket("Boombastic"):
print(f"Here is your flag : {FLAG}, enjoy the movie sir.")
else:
print("Sorry, VIPs only.")
sys.exit()
elif c == '2':
word = os.urandom(16).hex()
print(f"\nYour ticket : {dumps(get_ticket(word))}")
elif c == '3':
print("Goodbye :)")
sys.exit()
except Exception:
print("System error.")
sys.exit()
signal.alarm(360)
if __name__ == "__main__":
challenge = Boombastic()
challenge.start()
This challenge is pretty straightforward. When we choose option 2, a random unknown 16 byte ‘word’ is generated and then chucked into the get_ticket function where the word is hashed using SHA-256 and stored in y after which a series of modular calculations is performed (note that secret is a random number between 1 and a strong 1024 bit prime p generated by the server) :
The prime p along with the values r and s are returned by the server. Our objective is to predict the 'ticket' (i.e. the p, r and s values) of the word 'Boombastic'. Since the prime p and secret is constant per server session we already have that. Recently, we learned of something known as a Gröbner basis where it is defined for ideals (an ideal of a ring is a special subset of its elements) in a polynomial ring R = K[x1, x2, x3, ..., xn], over a field K.
Although the theory works for any field, most Gröbner basis computations are done either when K is the field of rationals or the integers modulo a prime number as it is in our case. Our ideal would be a relation of the given equations above so for the first one, r - (y2 - 1) * k2 and the second one being s - (y + 1) * k where k represents the modular multiplicative inverse of the secret with respect to the prime p. Hence we could use the inbuilt Sage function for the Gröbner basis to recover the secret and hence the r and s values.
Our Sage solve script :
from pwn import *
import json
from Crypto.Util.number import getStrongPrime, inverse
import hashlib, sys, os, signal, random
local = False
debug = False
if local:
tube = process(["python3", "server.py"], level='debug') if debug else process(["python3", "server.py"])
else:
tube = remote("52.149.135.130", 4872, level = 'debug') if debug else remote("52.149.135.130", 4872)
tube.sendlineafter("> ", b"2")
tube.recvline()
output = json.loads(tube.recvline()[14:].decode())
s, r, p = int(output['s'], 16), int(output['r'], 16), int(output['p'], 16)
y, k = gens(PolynomialRing(Zmod(p), ['y','k']))
ideal = [r - (y^2 - 1)*k^2, s - (y + 1)*k]
I = Ideal(ideal)
B = I.groebner_basis()
#print(B[0])
#print(B[1])
k = int(-B[1](k = 0)) % p
secret = inverse_mod(k, p)
print(secret)
y = int((-B[0](y = 0))) % p
#print(y)
def get_ticket(code):
y = int(hashlib.sha256(code.encode()).hexdigest(),16)
r = ((y**2 - 1) * (inverse(secret**2, p))) % p
s = ((1 + y) * (inverse(secret, p))) % p
return str({'s': hex(s), 'r': hex(r), 'p': hex(p)})
payload = get_ticket("Boombastic").replace("'", '"')
tube.sendlineafter("> ", b"1")
tube.sendlineafter('Enter the magic word : ', payload.encode())
print(tube.recvline())
exit()
And after running the script, we recovered the secret and hence the flag :

Flag : FwordCTF{4ct_l1k3_a_V1P_4nd_b3c0m3_a_V1P}
Leaky Blinders
The server source code provided :
#!/usr/bin/env python3.8
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import sys, os
FLAG = b"FwordCTF{###############################################################}"
WELCOME = '''
Welcome to Enc/Dec Oracle.
'''
key = os.urandom(32)
def xor(a, b):
return bytearray([a[i % len(a)] ^ b[i % len(b)] for i in range(max(len(a), len(b)))])
def encrypt(msg):
aes = AES.new(key, AES.MODE_ECB)
if len(msg) % 16 != 0:
msg = pad(msg, 16)
cipher = aes.encrypt(msg)
cipher = xor(cipher, key)
return cipher
def decrypt(cipher, k):
aes = AES.new(k, AES.MODE_ECB)
cipher = xor(cipher, k)
msg = unpad(aes.decrypt(cipher), 16)
return msg
class Leaky_Blinders:
def __init__(self):
print(WELCOME + f"Here is the encrypted flag : {encrypt(FLAG).hex()}")
def start(self):
try:
while True:
print("\n1- Encrypt")
print("2- Decrypt")
print("3- Leave")
c = input("> ")
if c == '1':
msg = os.urandom(32)
cipher = encrypt(msg)
if all(a != b for a, b in zip(cipher, key)):
print(cipher.hex())
else:
print("Something seems leaked !")
elif c == '2':
k = bytes.fromhex(input("\nKey : "))
cipher = bytes.fromhex(input("Ciphertext : "))
flag = decrypt(cipher, k)
if b"FwordCTF" in flag:
print(f"Well done ! Here is your flag : {FLAG}")
else:
sys.exit("Wrong key.")
elif c == '3':
sys.exit("Goodbye :)")
except Exception:
sys.exit("System error.")
if __name__ == "__main__":
challenge = Leaky_Blinders()
challenge.start()
This was a really weird challenge. In option 2, we are asked to provide a key and ciphertext which is then decrypted by the server. If the bytes “FwordCTF” are found in the decrypted text, we get the flag so that is exactly what we did, we made a key and encrypted the word “FwordCTF{leaky_blinders}” using the encryption function provided by the server and passed that key and ciphertext over to get the flag.
Our solve script :
from pwn import *
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
local = False
debug = False
if local:
r = process(["python3", "leaky_blinders.py"], level='debug') if debug else process(["python3", "leaky_blinders.py"])
else:
r = remote("52.149.135.130", 4869, level = 'debug') if debug else remote("52.149.135.130", 4869)
key = bytes.fromhex("deadbeefdeadbeefdeadbeefdeadbeef")
def xor(a, b):
return bytearray([a[i % len(a)] ^ b[i % len(b)] for i in range(max(len(a), len(b)))])
def encrypt(msg):
aes = AES.new(key, AES.MODE_ECB)
if len(msg) % 16 != 0:
msg = pad(msg, 16)
cipher = aes.encrypt(msg)
cipher = xor(cipher, key)
return cipher
ct = encrypt(b"FwordCTF{leaky_blinders}")
r.sendlineafter(b"> ", b"2")
r.sendlineafter(b"Key : ", b"deadbeefdeadbeefdeadbeefdeadbeef")
r.sendlineafter(b"Ciphertext : ", ct.hex())
print(r.recvline())
exit()
Flag : FwordCTF{N3v3r_x0r_w1thout_r4nd0m1s1ng_th3_k3y_0r_m4yb3_s3cur3_y0ur_c0d3}
Welcome
Find the flag in the Discord server.
Flag : FwordCTF{Welcome_To_FwordCTF_2021}