
We competed in the 2021 Zh3r0 CTF V2 CTF event (Fri, 04 June 2021, 18:30 SGT — Sun, 06 June 2021, 18:30 SGT). We ranked 48th out of 509 scoring teams as a 3 person team.
I managed to solve only 2 challenges (I need to learn so much more….) and both were under the cryptography category (first time solving a cryptography CTF challenge). This was the first time that I played with my friend Diamondroxxx for the entire duration of a CTF (he had joined towards the end for UMass and Angstrom).

Here are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
| 1n-Jection | Crypto | 304 | 45 |
| Chaos | Crypto | 136 | 50 |
1n-Jection
This was the source code provided for the challenge :
from secret import flag
def nk2n(nk):
l = len(nk)
if l==1:
return nk[0]
elif l==2:
i,j = nk
return ((i+j)*(i+j+1))//2 +j
return nk2n([nk2n(nk[:l-l//2]), nk2n(nk[l-l//2:])])
print(nk2n(flag))
#2597749519984520018193538914972744028780767067373210633843441892910830749749277631182596420937027368405416666234869030284255514216592219508067528406889067888675964979055810441575553504341722797908073355991646423732420612775191216409926513346494355434293682149298585
So the encryption function was provided nk2n() and the flag ciphertext was also provided (the commented large integer). So we had to reverse this encryption process from the ciphertext to the flag itself.
The function encrypts text by taking in a list of ASCII characters. It then checks if the length of that list is 1 or 2. If it is 1, it returns the element itself (as list length is 1) and if it is 2, it would return ((i+j)*(i+j+1))//2 +j. Since the first element is i and second element is j, doing (i + j) * (i + j + 1) gives an even number which is then divided by 2 (floor division). Then the second element is added.
This function also recursively calls itself as shown in the last return statement. So it first divides the list into two parts so for example if the list had 5 elements, the first part would be the first 3 elements and the second part would be the last 2 elements (for list length of 4 it would be 2 and 2 for the splits). It then calls itself (nk2n) with each split or half and repeats the process until the base case of length equals 1 or 2 and finally the ciphertext is outputted.
Here is an example of how it works with the test input flag of “zh3r0{}” :
flag = [122, 104, 51, 114, 48, 123, 125]
#z h 3 r 0 { }
#122 104 51 114 48 123 125
def nk2n(nk):
l = len(nk)
if l==1:
print("l == 1 : ", "returning:", nk)
return nk[0]
elif l==2:
#print("l ==2:", nk)
i,j = nk
print("l == 2 :", nk, "returning:", ( (i+j) * (i+j+1) ) // 2 + j)
return ( (i+j) * (i+j+1) ) // 2 + j
#print("nk2n[:", l-l//2, "] nk2n[", l-l//2, ":]")
print("First half : ", nk[:l-l//2], "Second half :", nk[ l-l//2:])
return nk2n( [ nk2n(nk [:l-l//2] ) , nk2n(nk[ l-l//2:] ) ] )
print("The encrypted flag is : ", nk2n(flag))
And when you test this, you can see how the function keeps splitting the input into half into two halves until the base case of list length 1 or 2 is reached :
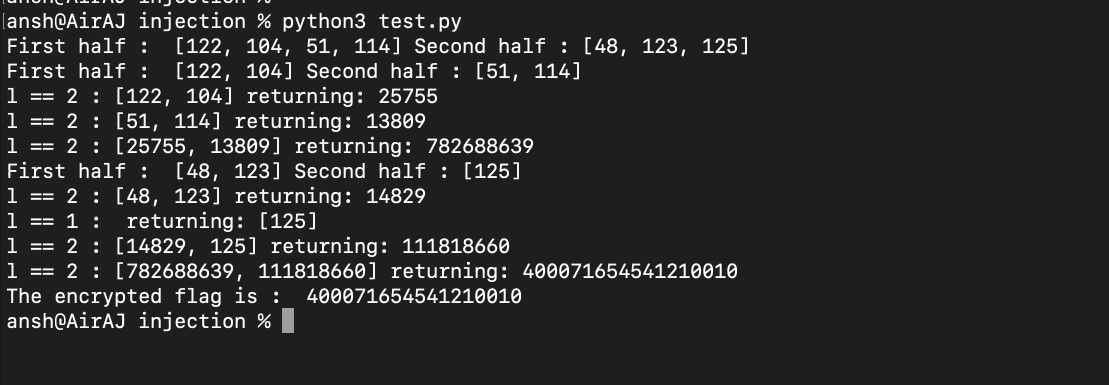
So what we have to do is first split the original input into the two previous halves and for each of those halves split them into further two halves until we reach a list of ASCII printable characters (so from ints 32 to 126).
Suppose we start with the input (n) and we need to split it into the two previous halves i and j :
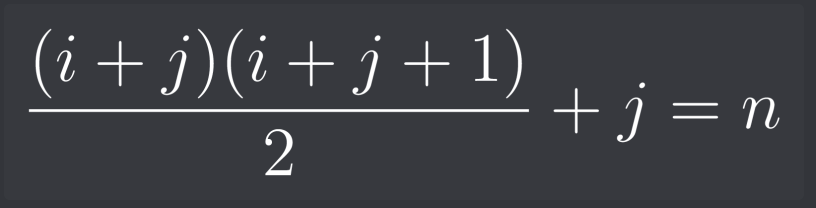
I noticed than when multiplying the equation by 2, (i + j) equals the square root of 2n. So we can now find j :
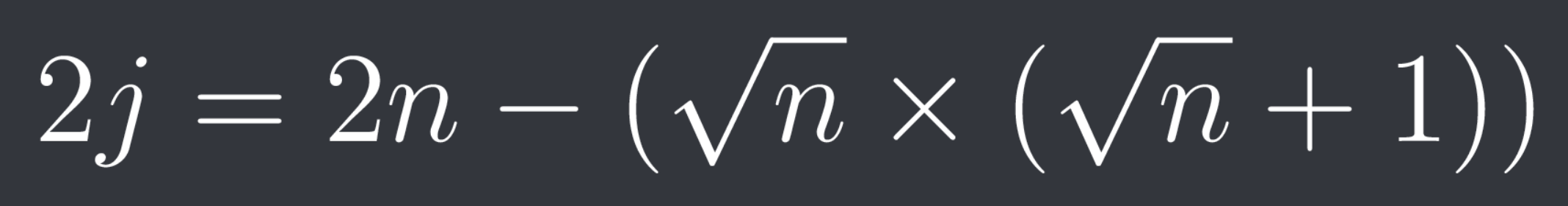
After dividing the above by 2, we get j. So with that we can get i, it is just the square root of n minus j (as the root of n is i + j). And with that we have split the input into its two previous splits or halves. With that, we could create a function which takes in an input and splits it into the two previous halves. We could repeat this process until we split our original input into a list of only ASCII printable characters (so if we had a certain element lying in the range 32 to 126, we wouldn’t split it further).
One problem that I came across is that sometimes I would get a negative value for j (which probably came because there are two solutions for j (negative and positive) and the negative one happened to be solved for). So my teammate noticed that in these cases where j was negative, the value of i was one less than the absolute value of j. So we solved for i by multiplying j by -1 (as j was negative) and then subtracting 1. With that we have i and we could then calculate j as j equals the equation below (and we know i and n) :
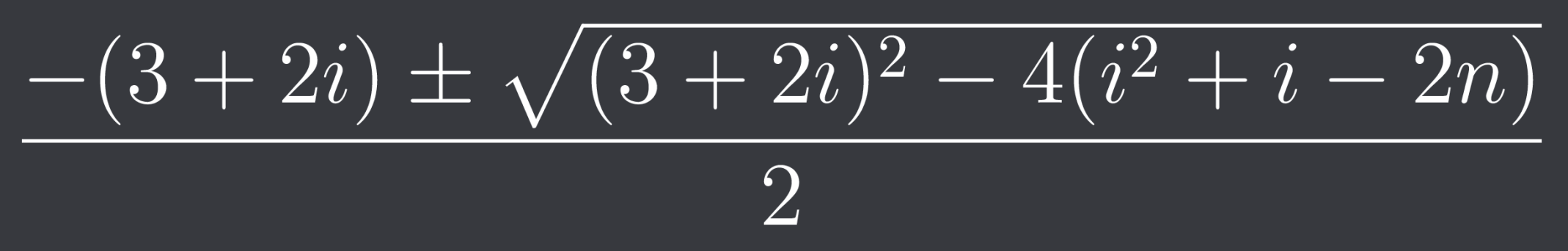
To obtain j, we formed a quadratic equation in terms of j from (i + j) (i + j + 1) + 2j = 2n as shown above (note that we only solved for the positive solution using the quadratic formula as j has to be positive). And with that we now know how to keep splitting each input further and further until we get a list of ASCII characters which is the flag.
This was my solution script :
import math
from itertools import chain
def nk2n(nk):
l = len(nk)
if l==1:
return nk[0]
elif l==2:
i,j = nk
return ((i+j)*(i+j+1))//2 +j
return nk2n([nk2n(nk[:l-l//2]), nk2n(nk[l-l//2:])])
_1_50 = 1 << 50 # 2**50 == 1,125,899,906,842,624
def isqrt(x):
if x < 0:
raise ValueError('square root not defined for negative numbers')
if x < _1_50:
return int(math.sqrt(x)) # use math's sqrt() for small parameters
n = int(x)
if n <= 1:
return n # handle sqrt(0)==0, sqrt(1)==1
r = 1 << ((n.bit_length() + 1) >> 1)
while True:
newr = (r + n // r) >> 1 # next estimate by Newton-Raphson
if newr >= r:
return r
r = newr
def quadraticFormulaPositive(a, b, c):
t1 = (-1) * b
discriminant = (pow(b, 2)) - (4) * a * c
t4 = math.sqrt(discriminant)
return int( (t1) + t4 ) // ( 2 * a)
def nextPrevious2(n):
n2 = 2 * n
pPlusq = isqrt(n2)
j2 = n2 - (pPlusq)*(pPlusq+1)
if (j2 < 0):
i = ( (-1) * j2//2 ) - 1
c = pow(i, 2) + i -n2
j = quadraticFormulaPositive(1, (3 + 2*i), c)
return [i, j]
j = j2//2
i = pPlusq - j
check = ( (i + j) * (i + j + 1) ) // 2 + j
#print(check - n)
return [i, j]
input = 2597749519984520018193538914972744028780767067373210633843441892910830749749277631182596420937027368405416666234869030284255514216592219508067528406889067888675964979055810441575553504341722797908073355991646423732420612775191216409926513346494355434293682149298585
masterList = nextPrevious2(input)
print("Initial 2 splits : ", masterList)
while (nk2n(masterList) == input):
previousMasterList = masterList
tempList = []
allless = True
for i in range(len(masterList)):
#print("element i:", masterList[i])
if masterList[i] > 126:
tempList.append(nextPrevious2(masterList[i]))
allless = False
else:
tempList.append([masterList[i],])
#print("TL:", tempList)
masterList = list(chain.from_iterable(tempList))
if allless:
break
print("ML:", masterList)
print("Flag ASCII List Is : ", previousMasterList)
flag = ""
for i in range(len(previousMasterList)):
flag = flag + chr(previousMasterList[i])
print(flag)
And after running the script (you can see how the original input is split into its halves and so on until you reach the flag - list of ASCII characters) :
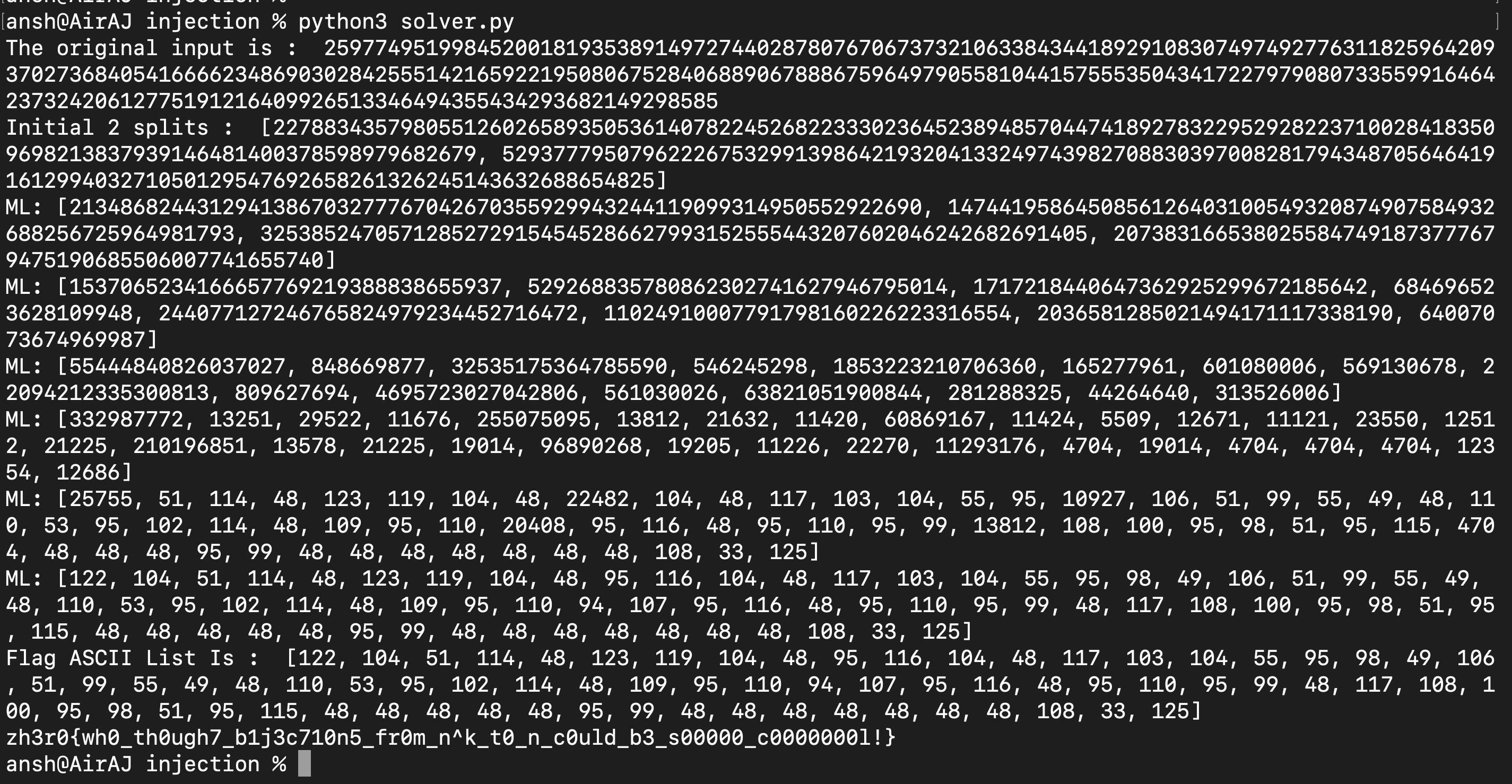
Flag : zh3r0{wh0_th0ugh7_b1j3c710n5_fr0m_n^k_t0_n_c0uld_b3_s00000_c0000000l!}
Chaos
This was the source code provided for the challenge :
from secret import flag
def ROTL(value, bits, size=32):
return ((value % (1 << (size - bits))) << bits) | (value >> (size - bits))
def ROTR(value, bits, size=32):
return ((value % (1 << bits)) << (size - bits)) | (value >> bits)
def pad(pt):
pt+=b'\x80'
L = len(pt)
to_pad = 60-(L%64) if L%64 <= 60 else 124-(L%64)
padding = bytearray(to_pad) + int.to_bytes(L-1,4,'big')
return pt+padding
def hash(text:bytes):
text = pad(text)
text = [int.from_bytes(text[i:i+4],'big') for i in range(0,len(text),4)]
M = 0xffff
x,y,z,u = 0x0124fdce, 0x89ab57ea, 0xba89370a, 0xfedc45ef
A,B,C,D = 0x401ab257, 0xb7cd34e1, 0x76b3a27c, 0xf13c3adf
RV1,RV2,RV3,RV4 = 0xe12f23cd, 0xc5ab6789, 0xf1234567, 0x9a8bc7ef
for i in range(0,len(text),4):
X,Y,Z,U = text[i]^x,text[i+1]^y,text[i+2]^z,text[i+3]^u
RV1 ^= (x := (X&0xffff)*(M - (Y>>16)) ^ ROTL(Z,1) ^ ROTR(U,1) ^ A)
RV2 ^= (y := (Y&0xffff)*(M - (Z>>16)) ^ ROTL(U,2) ^ ROTR(X,2) ^ B)
RV3 ^= (z := (Z&0xffff)*(M - (U>>16)) ^ ROTL(X,3) ^ ROTR(Y,3) ^ C)
RV4 ^= (u := (U&0xffff)*(M - (X>>16)) ^ ROTL(Y,4) ^ ROTR(Z,4) ^ D)
for i in range(4):
RV1 ^= (x := (X&0xffff)*(M - (Y>>16)) ^ ROTL(Z,1) ^ ROTR(U,1) ^ A)
RV2 ^= (y := (Y&0xffff)*(M - (Z>>16)) ^ ROTL(U,2) ^ ROTR(X,2) ^ B)
RV3 ^= (z := (Z&0xffff)*(M - (U>>16)) ^ ROTL(X,3) ^ ROTR(Y,3) ^ C)
RV4 ^= (u := (U&0xffff)*(M - (X>>16)) ^ ROTL(Y,4) ^ ROTR(Z,4) ^ D)
return int.to_bytes( (RV1<<96)|(RV2<<64)|(RV3<<32)|RV4 ,16,'big')
try:
m1 = bytes.fromhex(input("input first string to hash : "))
m2 = bytes.fromhex(input("input second string to hash : "))
if m1!=m2 and hash(m1)==hash(m2):
print(flag)
else:
print('Never gonna give you up')
except:
print('Never gonna let you down')
So as shown above, we have to input two different hex values but when their hash is calculated using the hash function shown above, their hashes have to be equal. This is a case of collisions in a chaotic hash function.
As stated in the above link, “Finally, observe that making (X,Y,Z,U) all 0xffffffff or all 0 results in the same output of the chaos function”. So if your first input (m1) corresponds to 0xffffffff, we need to reverse the second input (m2) to correspond to 0x00000000. This would be achieved by flipping the bits of the first input (a complementing collision).
So if my first input is “0124fdce89ab57eaba89370afedc45ef401ab257b7cd34e176b3a27cf13c3adf”, I need the flip each nibble (hex = 2 nibbles = 1 byte) and that will be my second input which would produce the same hash.
So I made a tiny script that does just that :
from pwn import *
m1 = "0124fdce89ab57eaba89370afedc45ef401ab257b7cd34e176b3a27cf13c3adf"
def flipBits(input):
m2 = ""
for i in range (len(m1)):
m2 = m2 + '{:x}'.format(~int(m1[i], 16) + 16)
return m2
m2 = flipBits(m1)
r = remote('crypto.zh3r0.cf', 2222)
r.sendlineafter("input first string to hash : ", m1)
r.sendlineafter("input second string to hash : ", m2)
flag = r.recvline()
print(flag)
And after running it, you get the flag :

Flag : zh3r0{something_chaotic_may_look_random_enough_but_may_be_not_sufficiently_secure}
Even though I managed to solve only 2 challenges over the span of this 2 day CTF, I learnt a lot about hash collisions and more importantly about how the RSA encryption system worked.
I failed to solve the Alice-Bob-Dave RSA challenge where the private exponent was given along with the public exponent and two ciphertexts (with a shared prime) yet I learnt so much about what the RSA encryption system was and how it worked. I spent so many frustrating hours on this challenge and when I finally saw the solution in this writeup, I was both sad that I couldn’t solve it whilst also glad that I could understand the solution at the same time.
I guess part of the learning journey is learning from your mistakes and other people and this holds true in CTFs as well. Hopefully for the next CTF, I will do better while still learning more new stuff :)