
Due to a lack of time or due to playing another CTF which was occuring at the same time, I couldn’t really spend much time at all for some CTFs. Below is the directory for some solve scripts for random cryptography challenges that I solved during the duration of such CTFs :
Below are the writeups :
| Challenge | CTF | Weight | Solves |
|---|---|---|---|
| oOoOoO | SECCON 2021 | 92.67 | 26/506 |
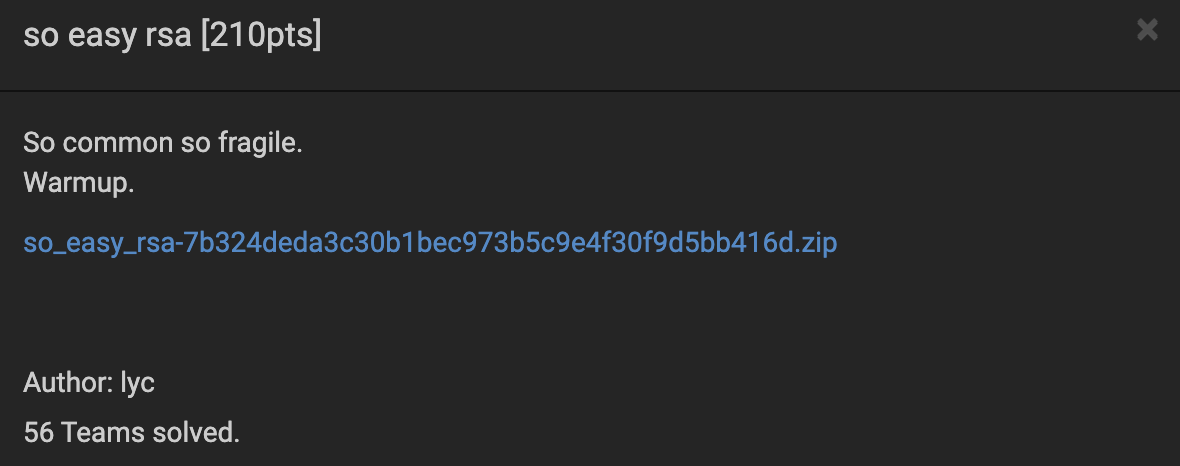
| So Easy RSA | HITCON 2021 | 88.98 | 56/288 |
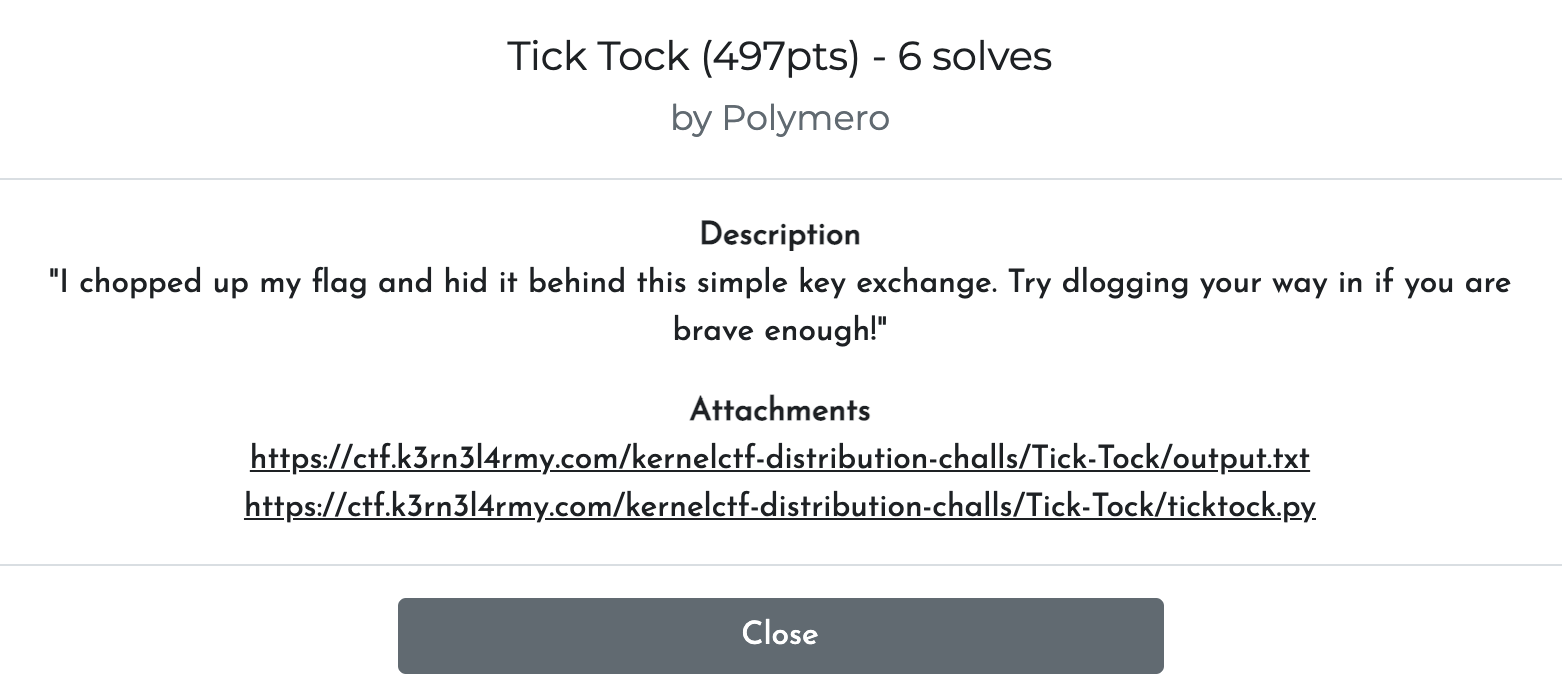
| Tick Tock 🩸 | K3RN3L 2021 | 24.37 | 6/501 |
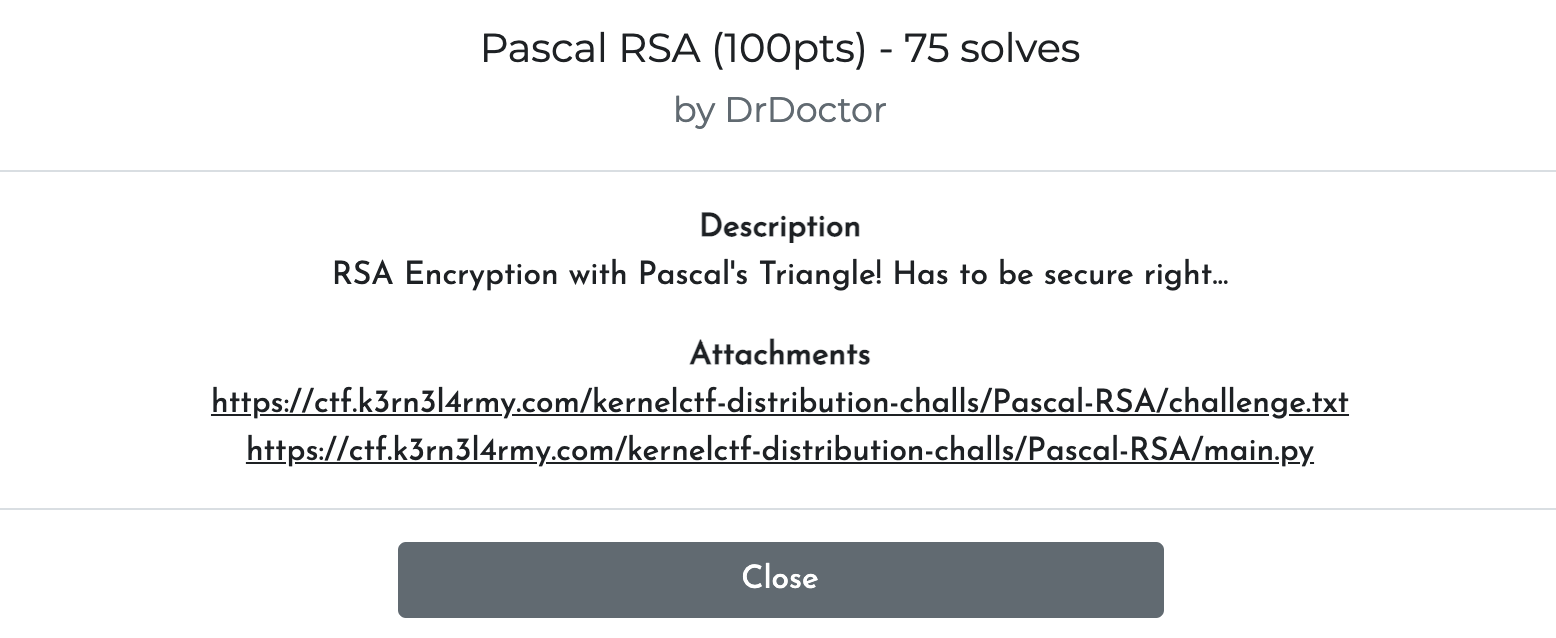
| Pascal RSA | K3RN3L 2021 | 24.37 | 75/501 |
| Pryby | K3RN3L 2021 | 24.37 | 96/501 |
| Spiritual | ASIS Quals 2021 | 89.22 | 60/741 |
| Crypto Warmup | ASIS Quals 2021 | 89.22 | 147/741 |
| Uncommon Factors II | RCTF 2021 | 69.20 | 29/483 |
Note : The “🩸” denotes first blood on that challenge.
SECCON 2021

Proof of solves during duration of CTF :

Joined 4 hours into CTF starting but was still 6th solve.
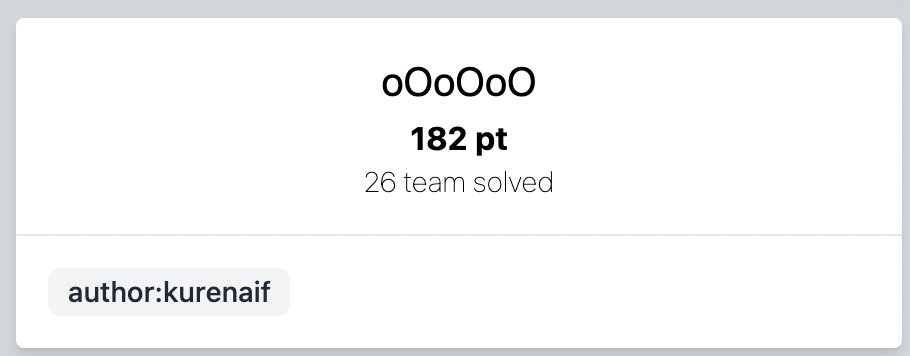
oOoOoO

Source Code provided :
import signal
from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime
import random
from flag import flag
message = b""
for _ in range(128):
message += b"o" if random.getrandbits(1) == 1 else b"O"
M = getPrime(len(message) * 5)
S = bytes_to_long(message) % M
print("M =", M)
print('S =', S)
print('MESSAGE =', message.upper().decode("utf-8"))
signal.alarm(600)
ans = input('message =').strip().encode()
if ans == message:
print(flag)
else:
print("🧙")
Solve script :
from sage.modules.free_module_integer import IntegerLattice
from Crypto.Util.number import bytes_to_long, long_to_bytes
# Directly taken from rbtree's LLL repository
# From https://oddcoder.com/LOL-34c3/, https://hackmd.io/@hakatashi/B1OM7HFVI
def Babai_CVP(mat, target):
M = IntegerLattice(mat, lll_reduce=True).reduced_basis
G = M.gram_schmidt()[0]
diff = target
for i in reversed(range(G.nrows())):
diff -= M[i] * ((diff * G[i]) / (G[i] * G[i])).round()
return target - diff
def solve(mat, lb, ub, weight = None):
num_var = mat.nrows()
num_ineq = mat.ncols()
max_element = 0
for i in range(num_var):
for j in range(num_ineq):
max_element = max(max_element, abs(mat[i, j]))
if weight == None:
weight = num_ineq * max_element
# sanity checker
if len(lb) != num_ineq:
print("Fail: len(lb) != num_ineq")
return
if len(ub) != num_ineq:
print("Fail: len(ub) != num_ineq")
return
for i in range(num_ineq):
if lb[i] > ub[i]:
print("Fail: lb[i] > ub[i] at index", i)
return
# heuristic for number of solutions
DET = 0
if num_var == num_ineq:
DET = abs(mat.det())
num_sol = 1
for i in range(num_ineq):
num_sol *= (ub[i] - lb[i])
if DET == 0:
print("Zero Determinant")
else:
num_sol //= DET
# + 1 added in for the sake of not making it zero...
print("Expected Number of Solutions : ", num_sol + 1)
# scaling process begins
max_diff = max([ub[i] - lb[i] for i in range(num_ineq)])
applied_weights = []
for i in range(num_ineq):
ineq_weight = weight if lb[i] == ub[i] else max_diff // (ub[i] - lb[i])
applied_weights.append(ineq_weight)
for j in range(num_var):
mat[j, i] *= ineq_weight
lb[i] *= ineq_weight
ub[i] *= ineq_weight
# Solve CVP
target = vector([(lb[i] + ub[i]) // 2 for i in range(num_ineq)])
result = Babai_CVP(mat, target)
for i in range(num_ineq):
if (lb[i] <= result[i] <= ub[i]) == False:
print("Fail : inequality does not hold after solving")
break
# recover x
fin = None
if DET != 0:
mat = mat.transpose()
fin = mat.solve_right(result)
## recover your result
return result, applied_weights, fin
from pwn import *
debug = False
r = remote("oooooo.quals.seccon.jp", 8000, level = 'debug' if debug else None)
r.recvuntil('M = ')
M = int(r.recvline().decode())
assert is_prime(M)
r.recvuntil('S = ')
S = int(r.recvline().decode())
k = (S - 79*sum(256^i for i in range(128))) * inverse_mod(32, M)
k = k % M
n = 129
MAT = [[0 for _ in range(n)] for _ in range(n)]
for i in range(n-1):
MAT[i][i] = 1
for j in range(n-1):
MAT[j][n-1] = 256^j
MAT[n-1][n-1] = M
MAT = Matrix(MAT)
lb = [0 for _ in range(n-1)] + [k]
ub = [1 for _ in range(n-1)] + [k]
res, weights, _ = solve(MAT, lb, ub)
msg = ''.join(["o" if x else "O" for x in res[:-1]])[::-1]
assert (bytes_to_long(msg.encode()) % M) == S
r.sendlineafter("message =", msg)
print(r.recvline())
#b'SECCON{Here_is_Huge-Huge_Island_yahhoOoOoOoOoOoO}\n'
Flag : SECCON{Here_is_Huge-Huge_Island_yahhoOoOoOoOoOoO}
HITCON 2021

Proof of solves during duration of CTF :

So Easy RSA
Source Code provided :
from gmpy2 import next_prime, is_prime
from random import randint
from Crypto.Util.number import bytes_to_long
class Rand:
def __init__(self):
self.seed = randint(2, 2**512)
self.A = next_prime(randint(2, 2**512))
self.B = next_prime(randint(2, 2**512))
self.M = next_prime(randint(2, 2**512))
for _ in range(10000):
self.next()
def next(self):
self.seed = self.seed * self.A + self.B
self.seed = self.seed % self.M
return self.seed
def __str__(self):
return f"{self.A}, {self.B}, {self.M}"
def gen_prime(r):
while True:
v = r.next()
if is_prime(v):
return v
r = Rand()
p,q = gen_prime(r), gen_prime(r)
n = p*q
e = 65537
flag = bytes_to_long(open('flag','rb').read())
val = pow(flag, e, n)
print(n)
print(r)
print(val)
The accompanying output file can be found here.
Used this link to solve. Solve script :
from Crypto.Util.number import *
from tqdm import tqdm
import cysignals
N = 198148795890507031730221728469492521085435050254010422245429012501864312776356522213014006175424179860455397661479243825590470750385249479224738397071326661046694312629376866307803789411244554424360122317688081850938387121934893846964467922503328604784935624075688440234885261073350247892064806120096887751
a, b, m = 1677936292368545917814039483235622978551357499172411081065325777729488793550136568309923513362117687939170753313352485633354858207097035878077942534451467, 5687468800624594128838903842767411040727750916115472185196475570099217560998907467291416768835644005325105434981167565207313702286530912332233402467314947, 1244793456976456877170839265783035368354692819005211513409129011314633866460250237897970818451591728769403864292158494516440464466254909969383897236264921
ct = 48071438195829770851852911364054237976158406255022684617769223046035836237425012457131162001786019505606941050117178190535720928339364199078329207393922570246678871062386142183424414041935978305046280399687623437942986302690599232729065536417757505209285175593543234585659130582659013242346666628394528555
e = 65537
def getFlag(p):
q = N // p
d = inverse(e, (q- 1) * (p - 1))
print(long_to_bytes(pow(ct, d, N)))
exit()
for k in tqdm(range(1, 10000)):
M = Integers(m)
A = M(a ^ k)
B = M(((a^k - 1) // (a - 1))*b)
try:
deltaSqrt1, deltaSqrt2 = Mod((B^2) + 4*A*N, m).sqrt(all=True)
p1 = int((-B + deltaSqrt1) * inverse_mod(int(2*A), m))
p2 = int((-B + deltaSqrt2) * inverse_mod(int(2*A), m))
except TypeError:
#print("Type error")
continue
except NotImplementedError:
#print("Not implemented hello")
continue
except cysignals.signals.SignalError:
continue
if N % p1 == 0:
getFlag(p1)
elif N % p2 == 0:
getFlag(p2)
else:
print("k not found :( ")
#b'hitcon{so_weak_randomnessssss}\n'
Flag : hitcon{so_weak_randomnessssss}
K3RN3L CTF 2021

Proof of solves during duration of CTF :

Tick Tock
Source Code provided :
from Crypto.Util.number import getPrime, isPrime
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
from random import randint
from hashlib import sha256
with open('flag.txt','rb') as f:
FLAG = f.read()
f.close()
assert len(FLAG) % 8 == 0
def legendre_symbol(a, p):
ls = pow(a, (p - 1) // 2, p)
return -1 if ls == p - 1 else ls
def modular_sqrt(a, p):
if legendre_symbol(a, p) != 1:
return 0
elif a == 0:
return 0
elif p == 2:
return p
elif p % 4 == 3:
return pow(a, (p + 1) // 4, p)
s = p - 1
e = 0
while s % 2 == 0:
s //= 2
e += 1
n = 2
while legendre_symbol(n, p) != -1:
n += 1
x = pow(a, (s + 1) // 2, p)
b = pow(a, s, p)
g = pow(n, s, p)
r = e
while True:
t = b
m = 0
for m in range(r):
if t == 1:
break
t = pow(t, 2, p)
if m == 0:
return x
gs = pow(g, 2 ** (r - m - 1), p)
g = (gs * gs) % p
x = (x * gs) % p
b = (b * g) % p
r = m
class TickTock:
def __init__(self, x, y, P):
self.x = x
self.y = y
self.P = P
assert self.is_on_curve()
def __repr__(self):
return '({}, {}) over {}'.format(self.x, self.y, self.P)
def __eq__(self, other):
return self.x == other.x and self.y == other.y and self.P == other.P
def is_on_curve(self):
return (self.x*self.x + self.y*self.y) % self.P == 1
def add(self, other):
assert self.P == other.P
x3 = (self.x * other.y + self.y * other.x) % self.P
y3 = (self.y * other.y - self.x * other.x) % self.P
return self.__class__(x3, y3, self.P)
def mult(self, k):
ret = self.__class__(0, 1, self.P)
base = self.__class__(self.x, self.y, self.P)
while k:
if k & 1:
ret = ret.add(base)
base = base.add(base)
k >>= 1
return ret
def lift_x(x, P, ybit=0):
y = modular_sqrt((1 - x*x) % P, P)
if ybit:
y = (-y) % P
return TickTock(x, y, P)
def domain_gen(bits):
while True:
q = getPrime(bits)
if isPrime(4*q + 1):
P = 4*q + 1
break
while True:
i = randint(2, P)
try:
G = lift_x(i, P)
G = G.mult(4)
break
except: continue
return P, G
def key_gen():
sk = randint(2, P-1)
pk = G.mult(sk)
return sk, pk
def key_derivation(point):
dig1 = sha256(b'x::' + str(point).encode()).digest()
dig2 = sha256(b'y::' + str(point).encode()).digest()
return sha256(dig1 + dig2 + b'::key_derivation').digest()
flagbits = [FLAG[i:i+len(FLAG)//8] for i in range(0,len(FLAG),len(FLAG)//8)]
for i in range(8):
print('# Exchange {}:'.format(i+1))
P, G = domain_gen(48)
print('\nP =', P)
print('G = ({}, {})'.format(G.x, G.y))
alice_sk, alice_pk = key_gen()
bobby_sk, bobby_pk = key_gen()
assert alice_pk.mult(bobby_sk) == bobby_pk.mult(alice_sk)
print('\nA_pk = ({}, {})'.format(alice_pk.x, alice_pk.y))
print('B_pk = ({}, {})'.format(bobby_pk.x, bobby_pk.y))
key = key_derivation(alice_pk.mult(bobby_sk))
cip = AES.new(key=key, mode=AES.MODE_CBC)
enc = cip.iv + cip.encrypt(pad(flagbits[i], 16))
print('\nflagbit_{} = "{}"'.format(i+1, enc.hex()))
print('\n\n\n')
The accompanying output.txt file can be found here. To solve this challenge, we implemented the steps outlined for the second case (page 5) where the Legendre symbol of the directrix of the ellipse with respect to the prime equals 1 as outlined in this paper.
The solve script :
from Crypto.Util.number import getPrime, isPrime
from Crypto.Util.Padding import pad
from Crypto.Cipher import AES
from random import randint
from hashlib import sha256
#https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.66.8688&rep=rep1&type=pdf
# Helper functions
def legendre_symbol(a, p):
ls = pow(a, (p - 1) // 2, p)
return -1 if ls == p - 1 else ls
def modular_sqrt(a, p):
if legendre_symbol(a, p) != 1:
return 0
elif a == 0:
return 0
elif p == 2:
return p
elif p % 4 == 3:
return pow(a, (p + 1) // 4, p)
s = p - 1
e = 0
while s % 2 == 0:
s //= 2
e += 1
n = 2
while legendre_symbol(n, p) != -1:
n += 1
x = pow(a, (s + 1) // 2, p)
b = pow(a, s, p)
g = pow(n, s, p)
r = e
while True:
t = b
m = 0
for m in range(r):
if t == 1:
break
t = pow(t, 2, p)
if m == 0:
return x
gs = pow(g, 2 ** (r - m - 1), p)
g = (gs * gs) % p
x = (x * gs) % p
b = (b * g) % p
r = m
# TickTock class
class TickTock:
def __init__(self, x, y, P):
self.x = x
self.y = y
self.P = P
assert self.is_on_curve()
def __repr__(self):
return '({}, {}) over {}'.format(self.x, self.y, self.P)
def __eq__(self, other):
return self.x == other.x and self.y == other.y and self.P == other.P
def is_on_curve(self):
return (self.x*self.x + self.y*self.y) % self.P == 1
def add(self, other):
assert self.P == other.P
x3 = (self.x * other.y + self.y * other.x) % self.P
y3 = (self.y * other.y - self.x * other.x) % self.P
return self.__class__(x3, y3, self.P)
def mult(self, k):
ret = self.__class__(0, 1, self.P)
base = self.__class__(self.x, self.y, self.P)
while k:
if k & 1:
ret = ret.add(base)
base = base.add(base)
k >>= 1
return ret
def lift_x(x, P, ybit=0):
y = modular_sqrt((1 - x*x) % P, P)
if ybit:
y = (-y) % P
return TickTock(x, y, P)
def domain_gen(bits):
while True:
q = getPrime(bits)
if isPrime(4*q + 1):
P = 4*q + 1
break
while True:
i = randint(2, P)
try:
G = lift_x(i, P)
G = G.mult(4)
break
except: continue
return P, G
def key_gen():
sk = randint(2, P-1)
pk = G.mult(sk)
return sk, pk
def key_derivation(point):
dig1 = sha256(b'x::' + str(point).encode()).digest()
dig2 = sha256(b'y::' + str(point).encode()).digest()
return sha256(dig1 + dig2 + b'::key_derivation').digest()
def phi(p):
a = Mod(-1, p.P).sqrt()
x, y = p.x, p.y
return x - a*y
P_List = [900301549573709, 935680375008173, 1055640765880517, 1080464169080837, 719079145687493, 621751256871989, 813572541888629, 1114531327051853]
G_List = [(536441147308213, 433384189616311), (752891243015718, 8106553512), (397997065626885, 489936393193239), (260443033023298, 803002953398154), (498571724307025, 703949890793665), (103410561193784, 578146374890578), (501548042112115, 51270153549450), (848718170467503, 890387510936812)]
A_pk_List = [(570766843177947, 254987309185033), (195456786203512, 260171210284077), (598336533181897, 679327572764649), (262506876458655, 717524579730657), (498097615872285, 458905235855936), (64283605936890, 59578661917638), (347207896856151, 99243054278463), (249185531830039, 1012351003599815)]
B_pk_List = [(359695429521403, 51578333245862), (899265030352476, 108212548527393), (68569414205977, 307720608649637), (905505250440203, 719592813122849), (596932104967, 584657608387075), (137204988087827, 594329296794969), (328307503789242, 154256166661670), (800057076995001, 999843105025038)]
flagbit_List = ["6a9517c4a5b9682676d014981651fbbdbd8b950cd5f3327c5dc2c733f0bad4d8", "ae98c526091bf8bcafab28527ce8ded895797048ec479cee35cd77d813116d86", "8860b181e0b91e5af755c64761283a16c8d9d5eee81c7cafa5d6810cc5896968", "394838402833e08299616048757c60dad287f74c8a27f2ad778ce57fdda41e41", "d64cd85f564b7394e6e9e2f59e10dbdf1780aa63a990bf3d685d7fad3d3afd15", "7c36b9779171251f34769955540837b1e913020b12e9fc418ffd7d654f9a1311", "0cc396078e17d21817d580cb90c380c584d4d5bc9d026868b9e4bc8e51364c95", "f044e34c66a93c35f612a8f949d5add77ff434e288139cda3573814b49229ab8"]
flag = ""
for i in range(8):
P = P_List[i]
G = TickTock(*G_List[i], P)
A_pk = TickTock(*A_pk_List[i], P)
B_pk = TickTock(*B_pk_List[i], P)
flagbit = flagbit_List[i]
A_u = Mod(phi(A_pk), P)
G_u = Mod(phi(G), P)
A_sk = A_u.log(G_u)
assert G.mult(A_sk) == A_pk
key = key_derivation(B_pk.mult(A_sk))
iv = bytes.fromhex(flagbit)[:16]
ct = bytes.fromhex(flagbit)[16:]
cip = AES.new(key=key, mode=AES.MODE_CBC, iv=iv)
flag += cip.decrypt(ct)[:-6].decode()
print(flag)
#flag{c0m1ng_up_w1th_4_g00d_fl4g_1s_qu1t3_d1ff1cult_und3r_4ll_th1s_t1m3_pr3ssur3}
We managed to first blood this challenge (at the time our time name was ‘ecc’) :


Flag : flag{c0m1ng_up_w1th_4_g00d_fl4g_1s_qu1t3_d1ff1cult_und3r_4ll_th1s_t1m3_pr3ssur3}
Pascal RSA
Source Code provided :
from Crypto.Util.number import getPrime,bytes_to_long
from math import gcd
flag = open('flag.txt','rb').read()
triangle =[[1]]
p = getPrime(20)
while len(triangle[-1]) <= p:
r = [1]
for i in range(len(triangle[-1]) - 1):
r.append(triangle[-1][i] + triangle[-1][i+1])
r.append(1)
triangle.append(r)
code = ''
for x in triangle[-1]:
code+=str(x%2)
d = int(code,2)
while True:
P = getPrime(512)
Q = getPrime(512)
if gcd(d, (P-1)*(Q-1)) == 1:
N = P*Q
e = pow(d,-1,(P-1)*(Q-1))
break
enc = pow(bytes_to_long(flag), e, N)
file = open('challenge.txt','w')
file.write(f'p = {p}\nenc = {enc}\nN = {N}')
The accompanying challenge.txt file can be found here. Use Lucas’s Theorem to solve. The solve script :
from Crypto.Util.number import *
#https://en.wikipedia.org/wiki/Lucas%27s_theorem
#https://github.com/Aakalpa/lucas-theorem-chinese-remainder-theorem-extended-euclid-algorithm/blob/master/lucas.py
# lucas theorem to calc C(n,r) % m if m is prime
memory = {} #creating a dictionary to store C(n,r,m) where 0<=r<=n<=9 .
# creating dictionary here also demonstrates memoization
p = 751921
def C(n,r,m):
if r < 0 or r > n : return 0
if r == 0 or r == n : return 1
if n > m :
return C(n%m,r%m,m) * C(n//m,r//m,m) % m
if (n,r,m) not in memory:
memory[(n,r,m)] = (C(n-1,r,m) + C(n-1,r-1,m)) % m #calculating C() recursively
return memory[(n,r,m)]
d = ""
for i in range(0, p+1):
d += str(C(p, i, 2))
d = int(d, 2)
enc = 9820620269072860401665805101881284961421302475382405373888746780467409082575009633494008131637326951607592072546997831382261451919226781535697132306297667495663005072695351430953630099751335020192098397722937812151774786232707555386479774460529133941848677746581256792960571286418291329780280128419358700449
N = 84317137476812805534382776304205215410373527909056058618583365618383741423290821410270929574317899945862949829480082811084554009265439540307568537940249227388935154641779863441301292378975855625325375299980291629608995049742243591901547177853086110999523167557589597375590016312480342995048934488540440868447
print(long_to_bytes(pow(enc, d, N)))
#b'flag{1ts_ch00se_a11_a10ng??}'
Flag : flag{1ts_ch00se_a11_a10ng??}
Pryby
The provided source code :
from Crypto.Util.number import bytes_to_long
def f(n):
q=[True]*(n + 1)
r=2
while r**2<=n:
if q[r]:
for i in range(r**2,n+1,r):q[i] = False
r += 1
return [p for p in range(2,n+1) if q[p]]
class G:
def __init__(self, f):
self.f = f
self.state = 1
def move(self):
q=1
for p in self.f:
if self.state%p!=0:
self.state=self.state*p//q
return
q*=p
flag = open('flag.txt','r').read().strip().encode()
flag=bytes_to_long(flag)
gen = G(f(pow(10,6)))
for _ in range(flag):gen.move()
print('enc =',gen.state)
# enc = 31101348141812078335833805605789286074261282187811930228543150731391596197753398457711668323158766354340973336627910072170464704090430596544129356812212375629361633100544710283538309695623654512578122336072914796577236081667423970014267246553110800667267853616970529812738203125516169205531952973978205310
The solve script :
from Crypto.Util.number import *
def f(n):
q=[True]*(n + 1)
r=2
while r**2<=n:
if q[r]:
for i in range(r**2,n+1,r):q[i] = False
r += 1
return [p for p in range(2,n+1) if q[p]]
enc = 31101348141812078335833805605789286074261282187811930228543150731391596197753398457711668323158766354340973336627910072170464704090430596544129356812212375629361633100544710283538309695623654512578122336072914796577236081667423970014267246553110800667267853616970529812738203125516169205531952973978205310
primes = f(pow(10, 6))
flag = 0
for i in range(len(primes)):
p = primes[i]
if enc % p == 0:
flag += 1 << i
print(long_to_bytes(flag))
#b'flag{functi0n_h4cking_ftw!}'
Flag : flag{functi0n_h4cking_ftw!}
ASIS Quals 2021

Proof of solves during duration of CTF :

Spiritual

The solve script :
from pwn import *
from Crypto.Util.number import *
debug = True
r = remote("168.119.108.148", 13010, level = 'debug' if debug else None)
#https://crypto.stackexchange.com/questions/27904/how-to-determine-the-order-of-an-elliptic-curve-group-from-its-parameters
def V_n(n, t, q):
a = 2
b = t
for i in range(2, n+1):
a, b = b, t*b-q*a
return b
while True:
r.recvuntil('p = ')
p = int(r.recvline())
assert isPrime(p)
r.recvuntil('k = ')
k = int(r.recvline())
r.recvuntil("What's the number of elements of E over finite field GF(p**n) where n = ")
n = int(r.recvline(keepends=False)[:-1])
print(n)
t = p + 1 - k
payload = p^n + 1 - V_n(n, t, p)
r.sendline(str(payload))
print(r.recvline())
#b'Congrats, you got the flag: .:: ASIS{wH47_iZ_mY_5P1R!TuAL_4NiMal!???} ::.\n'
Flag : ASIS{wH47_iZ_mY_5P1R!TuAL_4NiMal!???}
Crypto Warmup
The source code provided :
#!/usr/bin/env python3
from Crypto.Util.number import *
import string
from secret import is_valid, flag
def random_str(l):
rstr = ''
for _ in range(l):
rstr += string.printable[:94][getRandomRange(0, 93)]
return rstr
def encrypt(msg, nbit):
l, p = len(msg), getPrime(nbit)
rstr = random_str(p - l)
msg += rstr
while True:
s = getRandomNBitInteger(1024)
if is_valid(s, p):
break
enc = msg[0]
for i in range(p-1):
enc += msg[pow(s, i, p)]
return enc
nbit = 15
enc = encrypt(flag, nbit)
print(f'enc = {enc}')
The accompanying output file can be found here.
The solve script :
from Crypto.Util.number import *
import string
import ast
with open("output.txt", "r") as f:
temp = f.read()
enc = temp[6:]
p = len(enc)
assert isPrime(p)
def getAllPrimiteRoots(n):
f = Integers(n)
firstGenerator = f(primitive_root(n))
totient = euler_phi(n)
return [firstGenerator ^ i for i in range(1, totient) if gcd(i, totient) == 1]
primitiveRoots = getAllPrimiteRoots(p)
for s in primitiveRoots:
possibleFlag = 'AS'
for i in range(2, 5):
possibleFlag += enc[Integers(p)(i).log(s) + 1]
if possibleFlag != "ASIS{":
continue
for i in range(5, p-1):
possibleFlag += enc[Integers(p)(i).log(s) + 1]
print(possibleFlag[:64])
#ASIS{_how_d3CrYpt_Th1S_h0m3_m4dE_anD_wEird_CrYp70_5yST3M?!!!!!!}
Flag : ASIS{_how_d3CrYpt_Th1S_h0m3_m4dE_anD_wEird_CrYp70_5yST3M?!!!!!!}
RCTF 2021

Uncommon Factors II
The attached lN.bn file can be found here.
Source Code provided :
from multiprocessing import Pool
size = 2^7
flag = open("flag.txt", "rb").read()
assert len(flag) == 22
assert flag[:5] == b"flag{"
assert flag[-1:] == b"}"
seed = flag[5:-1] # 128 bit
seed = (int.from_bytes(seed,'big')<<104) + (randint(0,2^80)<<(128+104)) # 312 bit
ub = seed + 2^104
lb = seed
threads = 64
def f(i):
p = random_prime(ub, lbound=lb, proof=False)
q = random_prime(2**200, proof=False)
N = p*q
return N
def reseed(i):
set_random_seed()
pool = Pool(processes=threads)
pool.map(reseed,range(size))
lN = pool.map(f,range(size))
pool.close()
pool.join()
lN.sort()
with open("lN.bin","wb") as f:
for n in lN:
f.write(int(n).to_bytes(512//8,"big"))
Solve script :
from math import gcd
from os import SCHED_BATCH
from sage.all import ZZ
from sage.all import matrix
from Crypto.Util.number import long_to_bytes
SHARED_BITSIZE = 208
with open("lN.bin", "rb") as f:
combined = f.read()
Nlist = [int.from_bytes(combined[i:i+64], "big") for i in range(0, len(combined), 64)]
def factorize_msb(moduli, bitsize, shared_bitsize):
"""
Factorizes the moduli when some most significant bits are equal among multiples of a prime factor.
More information: Nitaj A., Ariffin MRK., "Implicit factorization of unbalanced RSA moduli" (Section 4)
:param moduli: the moduli
:param bitsize: the amount of bits of the moduli
:param shared_bitsize: the amount of shared most significant bits
:return: a list containing a tuple of the factors of each modulus, or None if the factors were not found
"""
L = matrix(ZZ, len(moduli), len(moduli))
L[0, 0] = 2 ** (bitsize - shared_bitsize)
for i in range(1, len(moduli)):
L[0, i] = moduli[i]
for i in range(1, len(moduli)):
L[i, i] = -moduli[0]
L = L.LLL()
for row in range(L.nrows()):
factors = []
for col in range(L.ncols()):
modulus = moduli[col]
q = gcd(L[row, col], modulus)
if 1 < q < modulus and modulus % q == 0:
factors.append((modulus // q, q))
if len(factors) == len(moduli):
return factors
factor_list = factorize_msb(Nlist, 512, SHARED_BITSIZE)
chosenp, _ = factor_list[-1]
flag = b"flag{" + long_to_bytes((chosenp >> 104) % 2^128) + b"}"
print(flag)
#b'flag{Simpl3_LLL_TrIck}'
Flag : flag{Simpl3_LLL_TrIck}