
During the weekend, I participated in Amrita University’s InCTF 2021 event (Fri, 13 Aug. 2021, 21:30 SGT — Sun, 15 Aug. 2021, 21:30 SGT). I was part of my new team Social Engineering Experts and we ranked 22nd out of 604 scoring teams. I managed to solve only 4 challenges, some in conjuction with Diamondroxxx who has also joined the team recently :

Timestamps for the challenges that I solved :
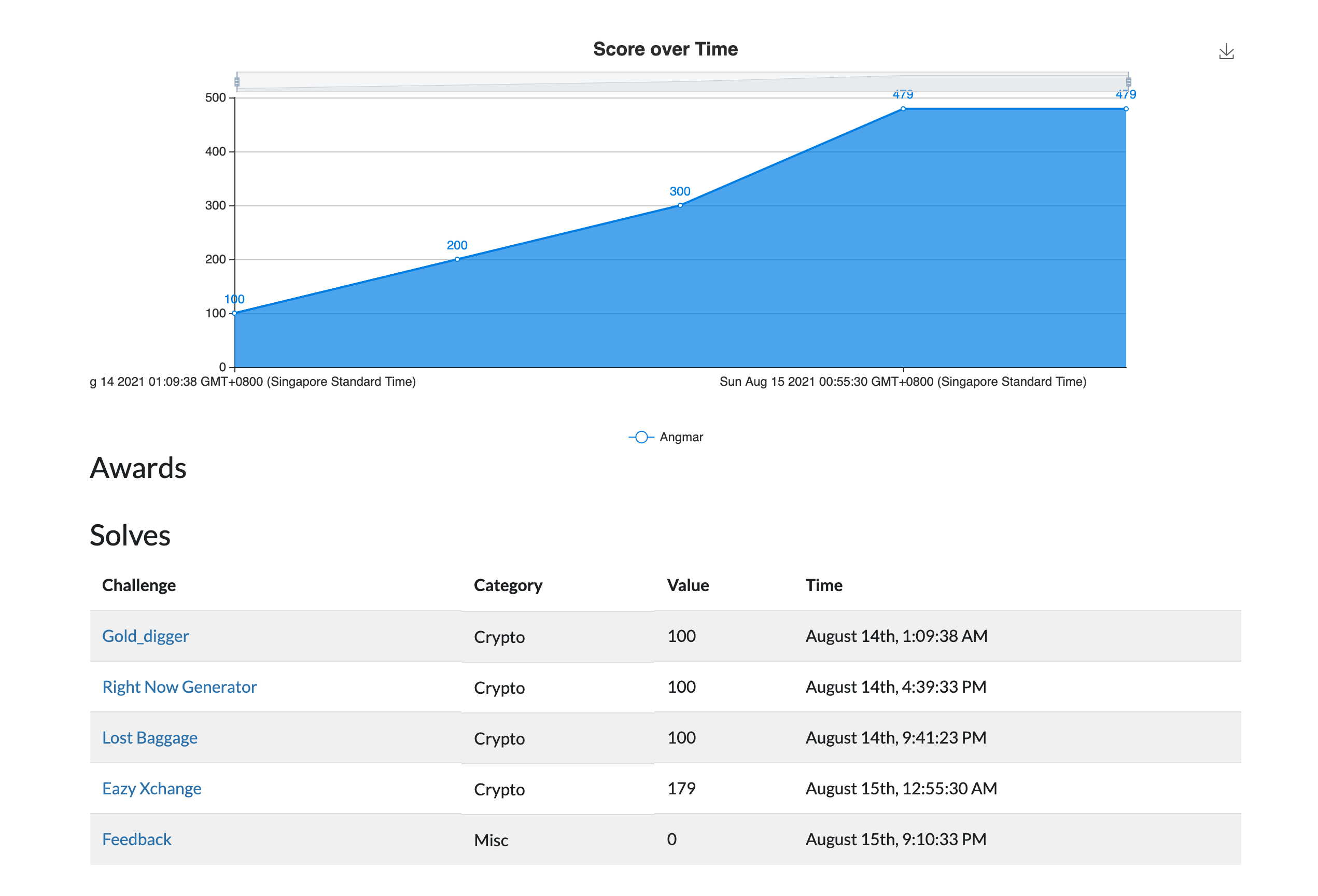
Below are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
| Eazy Xchange | Crypto | 179 | 44 |
| Right Now Generator | Crypto | 100 | 51 |
| Lost Baggage | Crypto | 100 | 52 |
| Gold Digger | Crypto | 100 | 76 |
Eazy Xchange
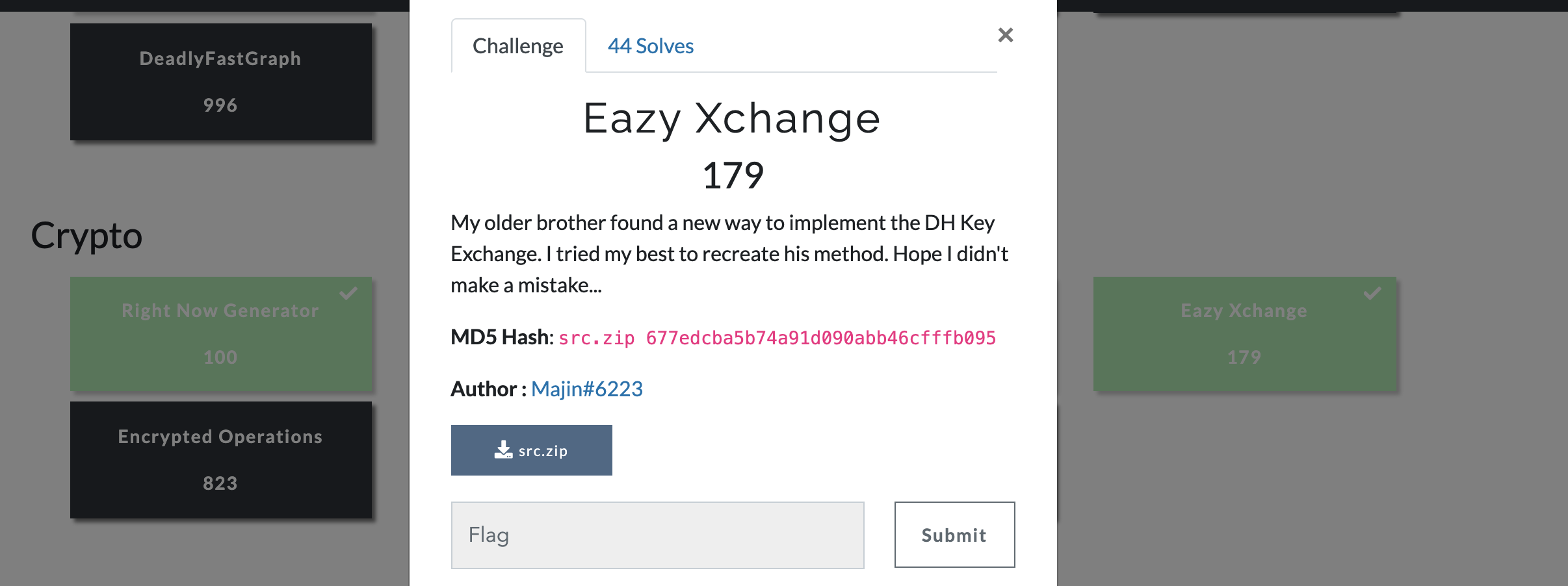
The Sage source code provided :
import os, hashlib, pickle
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
key = os.urandom(4)
FLAG = open('flag.txt', 'rb').read()
p = 0xFFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFF
a = p - 3
b = 0x5AC635D8AA3A93E7B3EBBD55769886BC651D06B0CC53B0F63BCE3C3E27D2604B
def gen_key(G, pvkey):
G = sum([i*G for i in pvkey])
return G
def encrypt(msg, key):
key = hashlib.sha256(str(key).encode()).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, os.urandom(16))
return {'cip': cipher.encrypt(pad(msg, 16)).hex(), 'iv': cipher.IV.hex()}
def gen_bob_key(EC, G):
bkey = os.urandom(4)
B = gen_key(G, bkey)
return B, bkey
def main():
EC = EllipticCurve(GF(p), [a, b])
G = EC.gens()[0]
Bx = int(input("Enter Bob X value: "))
By = int(input("Enter Bob Y value: "))
B = EC(Bx, By)
P = gen_key(G, key)
SS = gen_key(B, key)
cip = encrypt(FLAG, SS.xy()[0])
cip['G'] = str(G)
return cip
if __name__ == '__main__':
cip = main()
pickle.dump(cip, open('enc.pickle', 'wb'))
The file with the ciphertext and IV can be found here. The cryptosystem implemeted here is ECDH (Elliptic Curve Diffie-Hellman) key exchange. The gist of it can be seen in the image below :

The function gen_bob_key generates Bob’s private key dB but it has a serious vulnerability as it uses the function gen_key which returns the sum of 4 unknown bytes. Although there are 2564 possibilities for the 4 bytes, since the sum is returned as the private key, there can only be a maximum value of 1020 (255 * 4) with in-between values being different combinations of 4 bytes. Alice’s private key Da is also generated using gen_key hence it too will have only a maximum value of 1020.
Alice’s public key Qa is calculated by Qa = Da * G which is the result of adding G to itself d times as explained above. G or the generator point can be caluclated as curve parameters are given. By running two loops till 1020 in order to guess the correct private keys for both, the shared secret (SS) can be quickly calculated as SS = dB * Qa. Note that this is the x-coordinate of SS hence in the solve script, SS = dB * Qa.xy()[0] is used. From there, the shared secret can be used as the key to decrypt the AES-CBC ciphertext to get the flag.
The Sage solve script :
import pickle
import os, hashlib, pickle
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
with open("enc.pickle", "rb") as f:
given = pickle.load(f)
print(given)
ct = given["cip"]
givenIV = given["iv"]
p = 0xFFFFFFFF00000001000000000000000000000000FFFFFFFFFFFFFFFFFFFFFFFF
a = p - 3
b = 0x5AC635D8AA3A93E7B3EBBD55769886BC651D06B0CC53B0F63BCE3C3E27D2604B
EC = EllipticCurve(GF(p), [a, b])
G = EC.gens()[0]
def decrypt(key, msg):
key = hashlib.sha256(str(key).encode()).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, bytes.fromhex(givenIV))
return cipher.decrypt(msg)
for i in range(1021):
print(i)
#bobPrvKeyGuess = i
#i = 423 is answer
for alicePubKeyGuess in range(1021):
try:
SS = (i * alicePubKeyGuess * G).xy()[0]
flagGuess = decrypt(SS, bytes.fromhex(ct))
except ZeroDivisionError:
continue
if(flagGuess[:6] == b"inctf{"):
print("")
print(flagGuess)
exit(0)
Flag : inctf{w0w_DH_15_5o_c00l!_3c9cdad74c27d1fc}
Right Now Generator
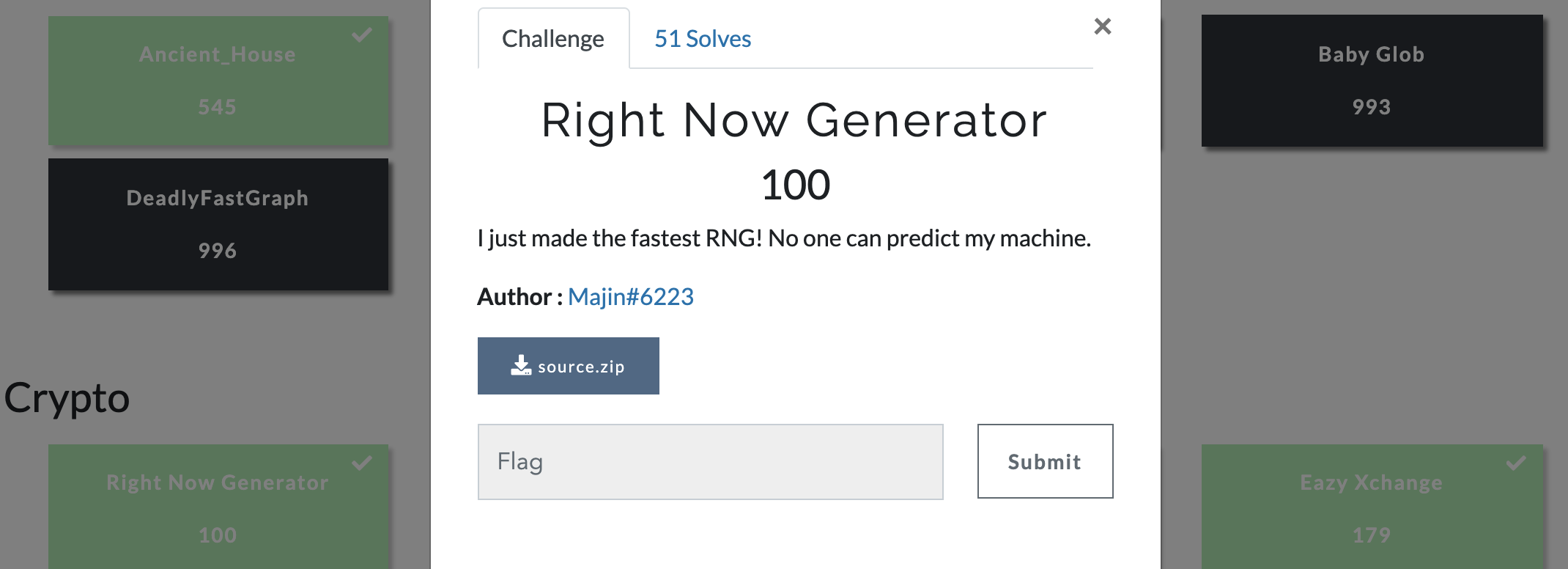
The source code provided :
#!/usr/bin/env python3
import random, hashlib, os, gmpy2, pickle
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
FLAG = open('flag.txt', 'rb').read()
class RNG():
pad = 0xDEADC0DE
sze = 64
mod = int(gmpy2.next_prime(2**sze))
def __init__(self, seed_val, seed=None):
if seed == None:
assert seed_val.bit_length() == 64*2, "Seed is not 128 bits!"
self.seed = self.gen_seed(seed_val)
self.wrap()
else:
self.seed = seed
self.ctr = 0
def gen_seed(self, val):
ret = [val % self.mod]
val >>= self.sze
for i in range(self.sze - 1):
val = pow(i ^ ret[i] ^ self.pad, 3, self.mod)
ret.append(val % self.mod)
val >>= self.sze
return ret
def wrap(self, pr=True):
hsze = self.sze//2
for i in range(self.sze):
r1 = self.seed[i]
r2 = self.seed[(i+hsze)%self.sze]
self.seed[i] = ((r1^self.pad)*r2)%self.mod
self.ctr = 0
def next(self):
a, b, c, d = (self.seed[self.ctr^i] for i in range(4))
mod = self.mod
k = 1 if self.ctr%2 else 2
a, b, c, d = (k*a-b)%mod, (b-c)%mod, (c-d)%mod, (d-a)%mod
self.ctr += 1
if self.ctr==64:
self.wrap(pr=False)
return a
def encrypt(key: bytes, pt: bytes) -> bytes:
key = hashlib.sha256(key).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, os.urandom(16))
return {'cip': cipher.encrypt(pad(pt, 16)).hex(), 'iv': cipher.IV.hex()}
def main():
obj = RNG(random.getrandbits(128))
out1 = ''.join([format(obj.next(), '016x') for i in range(64)])
out2 = ''.join([format(obj.next(), '016x') for i in range(64)])
cip = encrypt(bytes.fromhex(out1), FLAG)
cip['leak'] = out2
return cip
if __name__ == '__main__':
cip = main()
pickle.dump(cip, open('enc.pickle', 'wb'))
The file with the ciphertext, IV and leak can be found here. We have a RNG class which supposedly acts as a random number generator. Let’s break it down. The key for decrypting the ciphertext (AES-CBC where IV is given) is the variable out1. Our objective is to recover out1 given the leak which is the values of out2.
Firstly, a RNG object is created (denoted by obj in the source code), a constant prime number is used as shown by the line mod = int(gmpy2.next_prime(2**sze)). The value of this is 18446744073709551629 and will be denoted as P henceforth. The object is initialized with 16 random bytes (128 random bits) using the random library in Python. Since no seed is specified, after ensuring that the seed_val is 128 bits, the gen_seed function is called. This function isn’t really that important as all it returns is a list of 64 numbers by performing a series of calculations.
After that, the next method is called, four variables, a, b, c and d are calculated by the line a, b, c, d = (self.seed[self.ctr^i] for i in range(4)). After that, a series of modular operations is performed. There is a counter which increments each time next is called (out1 calls it 64 times). The variable k equals 1 if the counter is an even number else it is 2. Focusing just on a and b :
Note that if the counter reaches 64, the values of a are returned for out1 and out2 and then the wrap function is called which performs a series of operations shown in the source code above which transforms the original list of 64 numbers. So in our case, we have the 64 leaked a values for out2 and somehow we have to get to the transformed and ‘wrapped’ list of 64 numbers. After that, we have to reverse the operations performed in wrap after which we would reach the original list of 64 values used for out1 which is the key itself.
One thing I noticed after running the programs a few times and printing different values locally was that the first time next is called, a equals the first number in the list of 64 numbers and b equals the second number in that list. The second time next is called, a equals the second number and b equals the first number in the list. The third time it is called, a is the third number and b is the fourth and the fourth time it is called, a is the fourth number and b the third.
Hence thinking of it as pairs of two next calls, a is always the first number when the call (starting from 0 to 63) and hence counter is even (and k = 2) and b is always the first number when the counter (and call) is odd. This means that these two variables can be related in some way as they switch their values every 2 values.
First equation in the pair = \( ( 2a - b ) \ mod \ P\)
Second equation in the pair = \( ( b - a ) \ mod \ P\)
Remember that the values are switched for a and b in the second equation in the pair. I found that looking at each pair (counter even and counter odd and not) where l1 is the first leaked value in the pair and l2 the second leaked value in the pair :
If (2a - b) < P and (b - a) < P :
2a - b = l1
b - a = l2
If (2a - b) < P and (b - a) > P :
2a - b = l1
b - a = -(-l2 + P)
If (2a - b) > P and (b - a) < P :
2a - b = -(-l1 + P)
b - a = l2
Using Sage which can solve these systems of modular equations. I tested these 3 cases, whichever case returned a non-empty list was the real value for a and b. We can now recover the previous state which would provide us with the list of 64 wrapped numbers. To reverse the operations in wrap, a bit of knowledge regarding modular arithmetic is required. Let’s look at wrap :
The constant hsze is 64//2 which is 32. Each value in the list of 64 numbers is then looped through. r1 stores the value of the list corresponding to the counter in the loop and r2 stores the value of the counter + 32 modulo 64. So for the first run of the loop, r1 = 0 and r2 = 32, then r1 = 1 and r2 = 33 and so on. Once r1 = 32, r2 = (32 + 32) mod 64 which is 0 so the pair is reversed i.e. r1 = 32 and r2 = 0 (just like the first iteration in the loop). The wrapped value (wv) is calculated as follows (keeping in mind that the constant PAD = 0xDEADC0DE) :
Assuming that (r1 xor PAD) = x, r2 = y and the recovered wrap states k1 and k2 equals the returned value from the pair of opposites (like 0 and 32 for r1 and r2, and, 32 and 0 for r1 and r2) :
\[k_1 \equiv xy\ (\text{mod}\ P)\] \[k_2 \equiv yk_2\ (\text{mod}\ P)\]Since k1, k2 and P are known and keeping in mind that P is co-prime to k1 and k2, the modular multiplicative inverse can be used to recover x and y and hence r1 and r2 (i.e. the original out1 values which is the key).
A modular multiplicative inverse of an integer a with respect to the modulus P is a solution of the linear congruence :
\[ax \equiv 1\ (\text{mod}\ P)\]This congruence only holds if a and P are coprime (i.e. gcd(a, P) = 1). In our case, since P is prime the numbers are coprime hence the following equations can be derived (where inv(k1, P) denotes the modular multiplicative inverse of k1 with respect to P), found using a Crypto.Util.number package):
\[y \equiv (k_2 * inv(k_1, P) ) \ (\text{mod}\ P)\]Therefore r1 = y xor PAD. After recovering r1, similarly x can be found :
\[x \equiv (k_1 * inv(r1, P) ) \ (\text{mod}\ P)\]After recovering the original r2 as r2 = x xor PAD, the original 64 number list for out1 has been found. Now all that remains is joining the 64 numbers in hex into a single block and using the reconstructed out1 as a key to decrypt the ciphertext.
The Sage solve script :
import pickle
from Crypto.Util.Padding import pad, unpad
from Crypto.Util.number import inverse
import random, hashlib, os, gmpy2, pickle
from Crypto.Cipher import AES
with open("enc.pickle", "rb") as f:
given = pickle.load(f)
ct = given["cip"]
givenIV = given["iv"]
leak = given["leak"]
mod = 18446744073709551629
leakList = []
for i in range(64):
temp = leak[i*16:(i+1)*16]
leakList.append(temp)
def getOut2SeedValues(leak):
seedValues = []
for i in range(0, 64, 2):
leak1 = leakList[i]
leak2 = leakList[i + 1]
#print(f"Leak 1 = {leak1}, Leak 2 ={leak2}")
#print(f"Counter pair = {i}, {i+1}")
var('a, b')
#First positive, second negative
eq1 = 2*a-b == int(leak1, 16)
eq2 = b - a == -(-int(leak2, 16) + mod)
ans = solve([eq1, eq2], a, b, solution_dict=True)
dictAns = ans[0]
aValue, bValue = dictAns[a], dictAns[b]
if (ans != [] and aValue > 0 and bValue > 0):
dictAns = ans[0]
aValue, bValue = dictAns[a], dictAns[b]
seedValues.append(aValue)
seedValues.append(bValue)
continue
#First negative, second positive
eq1 = 2*a-b == -(-int(leak1, 16) + mod)
eq2 = b - a == int(leak2, 16)
ans = solve([eq1, eq2], a, b, solution_dict=True)
dictAns = ans[0]
aValue, bValue = dictAns[a], dictAns[b]
if (ans != [] and aValue > 0 and bValue > 0):
dictAns = ans[0]
aValue, bValue = dictAns[a], dictAns[b]
seedValues.append(aValue)
seedValues.append(bValue)
continue
#Both equations positive
eq1 = 2*a-b == int(leak1, 16)
eq2 = b - a == int(leak2, 16)
ans = solve([eq1, eq2], a, b, solution_dict=True)
dictAns = ans[0]
aValue, bValue = dictAns[a], dictAns[b]
if (ans != [] and aValue > 0 and bValue > 0):
dictAns = ans[0]
aValue, bValue = dictAns[a], dictAns[b]
seedValues.append(aValue)
seedValues.append(bValue)
continue
#print("Out 2 seed values : ", seedValues)
return seedValues
seedValuesOut2 = getOut2SeedValues(leak)
out1SeedValues = [0 for i in range(64)]
def getOut1Seed(out2Seed):
pad = int("0xDEADC0DE", 16)
sze = 64
hsze = sze//2
for i in range(32):
r1 = int(out2Seed[i])
r2 = int(out2Seed[(i+hsze)%sze])
y = (r2 * inverse(r1, mod)) % mod
realR1 = y ^^ pad
out1SeedValues[(i+hsze)%sze] = realR1
x = (r1 * inverse(realR1, mod)) % mod
realR2 = x ^^ pad
out1SeedValues[i] = realR2
getOut1Seed(seedValuesOut2)
#print(out1SeedValues)
finalOut1 = ""
for i in range(len(out1SeedValues)):
if (i % 2 == 0):
k = 2
a = out1SeedValues[i]
b = out1SeedValues[i + 1]
else:
k = 1
a = out1SeedValues[i]
b = out1SeedValues[i-1]
ans = (k*a - b) % mod
temp = hex(ans)[2:]
if(len(temp) < 16):
temp = ("0"*(16-len(temp)) + temp)
else:
pass
finalOut1 += temp
#print(i, ans, temp, len(temp))
#print(len(finalOut1), (i+1)*16)
#print("Len final out 1 :", len(finalOut1))
def decrypt(key: bytes, ct: bytes) -> bytes:
key = hashlib.sha256(key).digest()[:16]
cipher = AES.new(key, AES.MODE_CBC, bytes.fromhex(givenIV))
return cipher.decrypt(pad(ct, 16)).hex()
flag = decrypt(bytes.fromhex(finalOut1), bytes.fromhex(ct))
print(bytes.fromhex(flag))
Flag : inctf{S1mpl3_RN65_r_7h3_b35t!_b35e496b4d570c16}
Lost Baggage
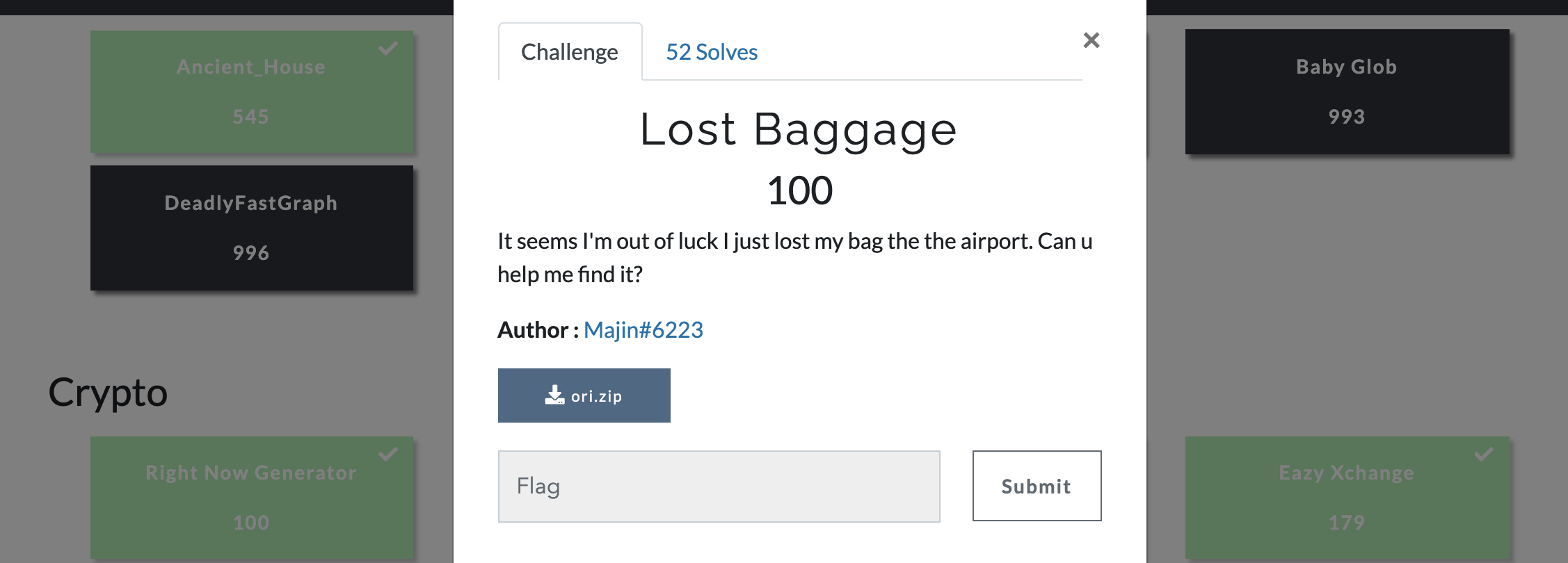
The source code provided :
#!/usr/bin/python3
from random import getrandbits as rand
from gmpy2 import next_prime, invert
import pickle
FLAG = open('flag.txt', 'rb').read()
BUF = 16
def encrypt(msg, key):
msg = format(int(msg.hex(), 16), f'0{len(msg)*8}b')[::-1]
assert len(msg) == len(key)
return sum([k if m=='1' else 0 for m, k in zip(msg, key)])
def decrypt(ct, pv):
b, r, q = pv
ct = (invert(r, q)*ct)%q
msg = ''
for i in b[::-1]:
if ct >= i:
msg += '1'
ct -= i
else:
msg += '0'
return bytes.fromhex(hex(int(msg, 2))[2:])
def gen_inc_list(size, tmp=5):
b = [next_prime(tmp+rand(BUF))]
while len(b)!=size:
val = rand(BUF)
while tmp<sum(b)+val:
tmp = next_prime(tmp<<1)
b += [tmp]
return list(map(int, b))
def gen_key(size):
b = gen_inc_list(size)
q = b[-1]
for i in range(rand(BUF//2)):
q = int(next_prime(q<<1))
r = b[-1]+rand(BUF<<3)
pb = [(r*i)%q for i in b]
return (b, r, q), pb
if __name__ == '__main__':
pvkey, pbkey = gen_key(len(FLAG) * 8)
cip = encrypt(FLAG, pbkey)
assert FLAG == decrypt(cip, pvkey)
pickle.dump({'cip': cip, 'pbkey': pbkey}, open('enc.pickle', 'wb'))
The file with the ciphertext and public keys can be found here. This system worked in the following ways. The function gen_key generates the public and private keys using the gen_inc_list function. What the latter function does is start off with a small prime number which is appended into a list. While the length of this list is not equal to the flag length times 8, a left bitwise shift is used to increase size of the prime which is then appended into this prime list.
Once this list has been returned, in gen_key, the last value of this prime list is stored in q. Again, a loop is ran a random 8 bit number times where q is further increased in size using left bit shifts (note that q is always prime as the next_prime method is called). After that, the final state or value of q is returned as part of the private key along with the prime list generated by gen_inc_list as well as a variable r which is calculated by adding a random number bitshifted to the left by 3 to the last prime returned from gen_inc_list. The public key is returned as a list of the length of the flag times 8 where looping through each prime b returned from gen_inc_list, the following public key is returned :
After playing around with the program a few times, I found some interesting properties. Nearly every single time, the final q value (the prime) was always larger than rb for even the largest values of b (the largest prime). This means that effectively if this is the case, the public key pb returns r * b. The first prime in the prime list for b always seemed to be less than 100,000 hence the value of r can be bruteforced. Assuming q to be larger than rb, by looping from 1 to 100,000, the values which perfectly divide the first public key would be be potential r values. This list of potential r values can be found by dividing the public key by the counter (i) in the loop which simulates rb / b to yield r. After running many times with known values, it always seemed that the last potential r value in this list was the correct r value.
Assuming that to be the correct value of r, by looping through the public key list and dividing each key by r (this effectively does rb / r to yield b), the list of primes returned by gen_inc_list i.e. b can be found (this is one of the three components of the private key). Now that b has been recovered, the final value of q is the last value in this b list and since r has been recovered first, we now have all 3 components of the private key. From there we can use the given decryption function by providing the private key which will then decrypt the ciphertext to yield the flag.
The Sage solve script :
import pickle
from gmpy2 import next_prime, invert
with open("enc.pickle", "rb") as f:
given = pickle.load(f)
ct = given["cip"]
pbkey = given["pbkey"]
flagSizeInBytes = len(pbkey)//8
#print(flagSizeInBytes)
def bruteForceR(smallPBkey):
possibleR = []
for i in range(1, 100000):
if (int(Mod(smallPBkey, i)) == 0):
possibleR.append(int(smallPBkey // i))
return possibleR
possibleRs = bruteForceR(pbkey[0])
mostLikelyR = possibleRs[-1]
bList = []
for i in range(flagSizeInBytes*8):
bList.append(pbkey[i] // mostLikelyR)
finalQ = bList[-1]
def decrypt(ct, pv):
b, r, q = pv
ct = (invert(r, q)*ct)%q
msg = ''
for i in b[::-1]:
if ct >= i:
msg += '1'
ct -= i
else:
msg += '0'
return bytes.fromhex(hex(int(msg, 2))[2:])
pv = (bList, mostLikelyR, finalQ)
flag = decrypt(ct, pv)
print(flag)
Flag : inctf{wr5_m4_b4g?}
Gold Digger
The source code provided :
import random
from Crypto.Util.number import *
flag=open("flag","rb").read()
def encrypt(msg, N,x):
msg, ciphertexts = bin(bytes_to_long(msg))[2:], []
for i in msg:
while True:
r = random.randint(1, N)
if gcd(r, N) == 1:
bin_r = bin(r)[2:]
c = (pow(x, int(bin_r + i, 2), N) * r ** 2) % N
ciphertexts.append(c)
break
return ciphertexts
N = 76412591878589062218268295214588155113848214591159651706606899098148826991765244918845852654692521227796262805383954625826786269714537214851151966113019
x = 72734035256658283650328188108558881627733900313945552572062845397682235996608686482192322284661734065398540319882182671287066089407681557887237904496283
flag = (encrypt(flag,N,x))
open("handout.txt","w").write("ct:"+str(flag)+"\n\nN:"+str(N)+"\n\nx:"+str(x))
The ciphertext list file can be found here.
The message is first converted to binary. Each bit is then looped through and a random number r between 1 and N is generated. If r and N are coprime, the ciphertext c is appended to a list. The ciphertext is generated by the following congruence (note that r is in binary and i is the current bit of the message being looped through) :
Since appending i to r and then converting to binary essentialy shifts r by 2, the ciphertext is actually :
\[c \equiv ( x^\text{2r + i} (\text{mod}\ N) * r^2 ) \ (\text{mod}\ N)\]Assuming that the current message bit (i) is 0 :
\[c \equiv ( x^\text{2r} (\text{mod}\ N) * r^2 ) \ (\text{mod}\ N)\] \[c \equiv ( (x^r)^\text{2} (\text{mod}\ N) * r^2 (\text{mod}\ N) ) \ (\text{mod}\ N)\]This looks awfully similar to a quadratic residue. In number theory, an integer q is called a quadratic residue modulo N if it is congruent to a perfect square modulo N; i.e., if there exists an integer x such that :
\[x^2 \equiv ( q ) \ (\text{mod}\ N)\]Otherwise, q is called a quadratic non-residue modulo N. In our case, we have two quadratic residues :
\[( (x^r)^\text{2} ) \ (\text{mod}\ N)\] \[( r^2 ) \ (\text{mod}\ N)\]An important property of quadratic residues is that the product of two quadratic residues modulo N is a quadratic residue modulo N which is exactly what we have here. So if the bit of the message (the flag) is a 0, we will have a quadratic residue and if we have a quadratic non-residue, the bit will be 1.
The Legendre symbol is usually used to check whether a number is a quadratic residue modulo an odd prime p but we obviously cannot use that here since N isn’t prime. Instead we could use the Jacobi Symbol which efficiently checks whether a number is a quadratic residue modulo an odd number N. If it is, 1 is returned else a 0 or -1 is returned. We could use that to check each bit and hence reconstruct the original flag.
The solve script :
import gmpy2
import ast
from Crypto.Util.number import long_to_bytes
N = 76412591878589062218268295214588155113848214591159651706606899098148826991765244918845852654692521227796262805383954625826786269714537214851151966113019
x = 72734035256658283650328188108558881627733900313945552572062845397682235996608686482192322284661734065398540319882182671287066089407681557887237904496283
with open("handout.txt", "r") as f:
temp = f.readlines()
ct = ast.literal_eval(temp[0][3:])
flag = ""
for cipherBit in ct:
if (gmpy2.jacobi(int(cipherBit), N) == 1):
flag += "0"
else:
flag += "1"
print(long_to_bytes(int(flag, 2)))
Flag : inctf{n0w_I_4in7_73ll1ng_u_4_g0ldd1gg3r}
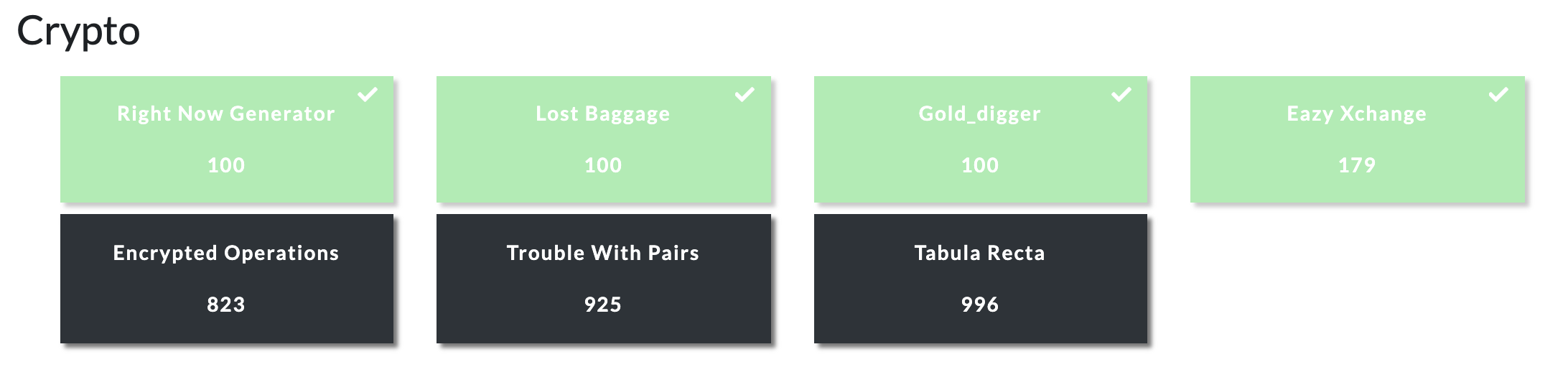
Honestly this was not a good CTF for me because the cryptography challenges that I solved were high in solves and low in points. I only managed to solve 4/7 crypto challenges :
I spent quite a bit on time on the BLS-signature challenge “Trouble With Pairs” but to no avail. I think I need to upgrade my cryptography knowledge by a decent bit now. I will be starting the book “An Introduction To Mathematical Cryptography” by Hoffstein, Pipher and Silverman in order to improve my foundational knowledge and understand cryptosystems better.