
I participated in the University of Tokyo’s TSG 2021 CTF event (Sat, 02 Oct. 2021, 15:00 SGT — Sun, 03 Oct. 2021, 15:00 SGT) during the weekend. Even though I am currently still in high school, I was invited to join the National University of Singapore’s CTF team, NUSGreyhats, by Diamondroxxx and we ranked 31st out of 775 scoring teams.
The reason why I am writing this as a blog post instead of a usual CTF writeup is because I could only solve the beginner’s crypto challenge and most of my time was spent solving the ECDSA biased nonce challenge ‘Flag Is Win’. However, due to an incredibly stupid mistake, me and Diamondroxxx only solved the challenge about 30 minutes after the CTF ended which really, really sucks.
The point of this blog post is to explain both to myself and others, how to crack the nonce of an ECDSA signature scheme if it does not have uniform random distribution and has low entropy by solving the Extended Hidden Number Problem (EHNP) using lattice reduction techniques.
Below is the writeup for the challenge Flag is Win :
Flag is Win
The server source code provided (written in Ruby) :
require 'openssl'
require 'digest'
STDOUT.sync = true
class OpenSSL::PKey::EC::Point
def xy
n = to_bn(:uncompressed).to_i
mask = (1 << group.degree) - 1
return (n >> group.degree) & mask, n & mask
end
alias_method :+, :add
alias_method :*, :mul
end
class ECDSA
def initialize
@curve = OpenSSL::PKey::EC::Group.new('secp256k1')
@G = @curve.generator
@n = @curve.order.to_i
@d = OpenSSL::BN.rand(@curve.degree).to_i
@Q = @G * @d
end
def inv(x)
x.pow(@n - 2, @n)
end
def sign(msg)
z = Digest::SHA256.hexdigest(msg).hex
k = OpenSSL::BN.rand(@curve.degree / 3).to_s.unpack1('H*').hex
x, y = (@G * k).xy
# We should discourage every evil hacks
s = (z + x * @d) * inv(k) % @n
return x, s
end
def verify(msg, x, s)
return false if x % @n == 0 || s % @n == 0
z = Digest::SHA256.hexdigest(msg).hex
# ditto
x2, y2 = (@G * (z * inv(s)) + @Q * (x * inv(s))).xy
return x == x2
end
end
ecdsa = ECDSA.new
5.times do
puts <<~EOS
1. Sign
2. Find rule
3. Exit
EOS
print 'choice? '
case gets.chomp
when '1'
x, s = ecdsa.sign('Baba')
puts 'Baba is:'
puts "x = #{x}"
puts "s = #{s}"
when '2'
print 'Which rule do you want to know? '; msg = gets.chomp
print 'x? '; x = gets.to_i
print 's? '; s = gets.to_i
if ecdsa.verify(msg, x, s)
if msg == 'Baba'
puts 'Baba is you'
elsif msg == 'Flag'
puts "Flag is #{ENV['FLAG']}"
else
puts 'Not Found :('
end
else
puts 'Invalid :('
end
else
exit
end
end
puts 'You is defeat.'
Looking at the source code, our task is pretty straightforward as our objective is to sign the SHA-256 hash of the word ‘Flag’. When connecting to the server, we are given 5 tries. In each try, we can either sign the word ‘Baba’ using ECDSA, provide a signature for a given message or exit the session. A standard curve secp256k1 is used. Obviously we would have to see what is going on with the signing mechanism used here.
ECDSA Recap
Remember that in elliptic curve cryptography, first a random number d is used as the private key by multiplying the generator or base point d times to reach some final public point Q.
Here is how to sign a message m using the private key IN ECDSA :
- Hash the message: \( h = SHA256(m) \)
- Sample a random nonce: \( k = n \qquad \qquad (n \in \mathbb{Z}^+) \)
- Exponentiate by the nonce: \( r = x_1 \mod n \)
- Reduce the x-coordinate mod the group order: \( r = x_1 \mod n \)
- Complete the signature: \( s = k^{-1} (h + r d) \mod n \)
- Signature is: \( \sigma = (r, s) \)
Biased Nonces
Looking at the sign function, we can see that the secret nonce k is generated really weirdly. To quote rkm0959’s writeup for the H1 challenge in Google CTF 2021, “The ECDSA nonce is yelling loudly at us to attack it which we obviously have to do.” Lmao
Usually the k should be a uniformally distributed random number however there is very low entropy over here. Note that while OpenSSL::BN.rand(@curve.degree / 3) does generate a large random 85 bit number, by appending .to_s.unpack1('H*'), a 3 is inserted to the left of every digit of this random number. The image below demonstrates this (the first value is the random number while the second is the number with the .to_s.unpack1('H*') added) :
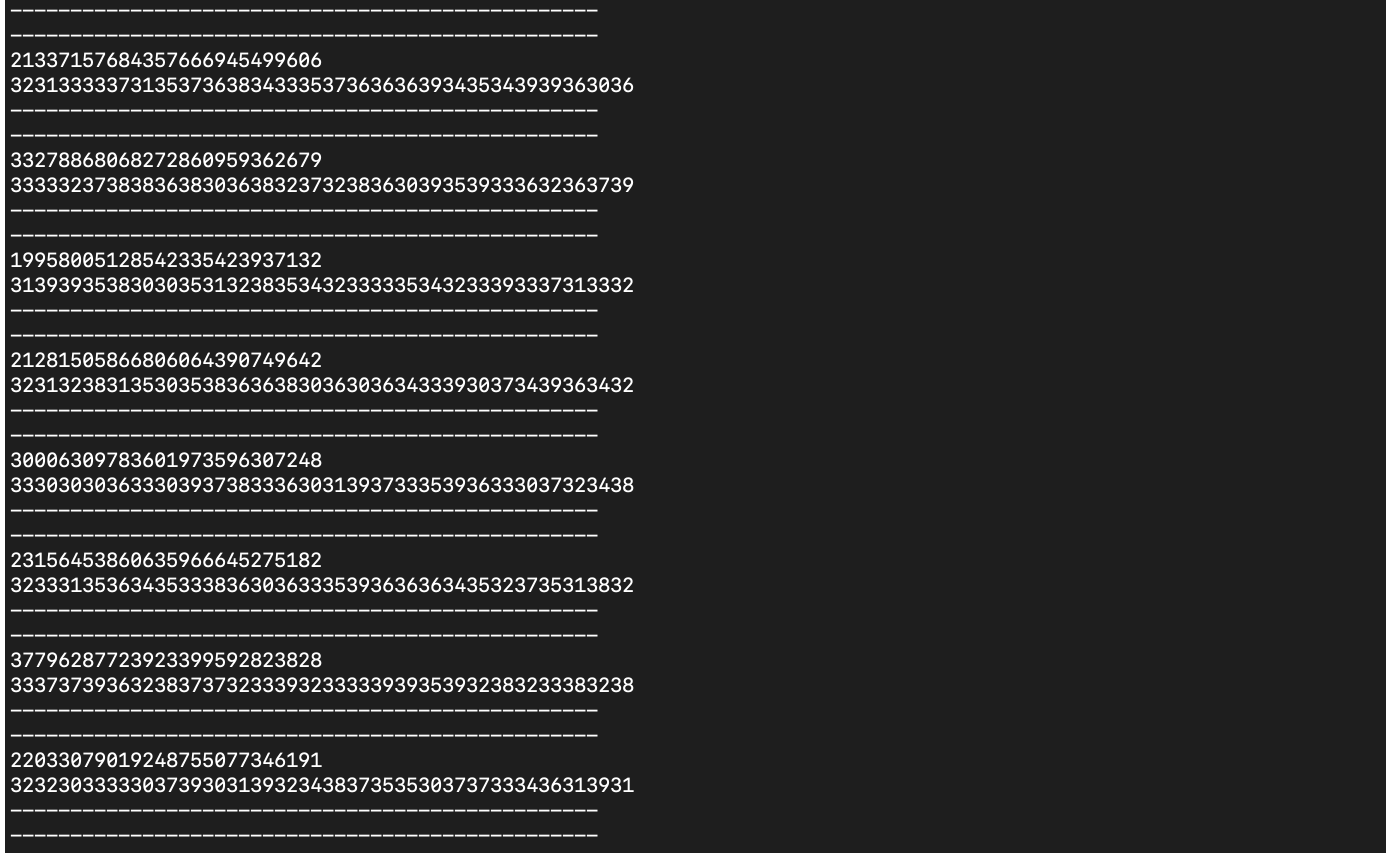
After that this number is converted to hexadecimal. Wow! So effectively only half of the bits of the nonce have entropy. That is very bad to say the least……
Deriving a Mathematical Expression For \( k \)
Firstly, we would have to come up with a precise mathematical expression for the nonce. Suppose that we consider the digits of k where \((0 \leq n \leq 9 )\).
We can rewrite this as a mix of binary and the unknown digits \( n \) where:
\[k = \quad 0011 \ n_{25} \quad 0011 \ x_{24} \quad 0011 \ x_{23} \quad .... \quad 0011 \ x_2 \quad 0011 \ x_1 \quad 3 \ x_0\]Now we can consider each byte of \( \quad 0011 \ n_{i} \quad \) where \(i \) represents some \(i^{th}\) bit from the LSB side:
\[B_i \quad = \quad 0011 \ n_i \quad = \quad 3 << 4 + n_i \quad = \quad 48 + n_i\]Now rewriting \(k\) we have:
\[k \ = \ B_{25} \quad B_{24} \quad B_{23} \quad .... \quad B_{2} \quad B_1 \quad B_0\] \[k \ = \ B_0 \quad + \quad B_1 << 2^{8*1} \quad + \quad B_2 << 2^{8*2} \quad + \quad .... \quad + \quad B_{24} << 2^{25*7} \quad + \quad B_{24} << 2^{25*8}\] \[\therefore k = \sum_{i=0}^{25} \ B_i \ \cdot 2^{8i}\] \[k = \sum_{i=0}^{25} \ (48 + n_i) \ \cdot 2^{8i}\] \[\therefore k = \sum_{i=0}^{25} \ 48 \ \cdot 2^{8i} \ + \ \sum_{i=0}^{25} \ n_i \ \cdot 2^{8i}\]Great, now we have an expression for the nonce k where a constant term and the unknown digit \( n_i \) are separated.
Cancelling Out the Private Key \( d \)
Now, consider the message, signature pair \( (r_1, s_1, h_1) \) and \( (r_2, s_2, h_1) \) where \( h_1 \) represents the SHA-256 hash of the word ‘Baba’. We know from the definition of ECDSA that:
\[s_1 = k_1^{-1} \ \cdot (h_1 + r_1 \ \cdot d)\] \[s_2 = k_2^{-1} \ \cdot (h_2 + r_2 \ \cdot d)\]Here we already obtained a mathematical expression for \( k \) hence:
\[\left( \sum_{i=0}^{25} \ 48 \ \cdot 2^{8i} \ + \ \sum_{i=0}^{25} \ n_i \ \cdot 2^{8i} \right) \cdot s_1 \equiv h_1 + r_1 d \pmod{n}\] \[\left( \sum_{i=0}^{25} \ 48 \ \cdot 2^{8i} \ + \ \sum_{i=0}^{25} \ n_i \ \cdot 2^{8i} \right) \cdot s_2 \equiv h_1 + r_2 d \pmod{n}\]Here \( n \) represents the prime used in this elliptic curve. Then, we can remove \( d \) from this set of equations. Since:
\(\quad \frac{k1 \ \cdot s_1 \ \ - \ h_1}{r_1} \quad \equiv d \pmod{n} \quad\) and \( \quad \frac{k2 \ \cdot s_2 \ \ - \ h_1}{r_2} \quad \equiv d \pmod{n} \)
\[\therefore \quad \quad \frac{k1 \ \cdot s_1 \ \ - \ h_1}{r_1} \quad \equiv \quad \frac{k2 \ \cdot s_2 \ \ - \ h_1}{r_2} \pmod{n}\] \[r_2 \ ( k_1 \ \cdot s_1 \ - \ h_1) \ \quad \equiv \quad r_1 \ ( k_2 \ \cdot s_2 \ - \ h_1) \pmod{n}\] \[r_2 \ \cdot k_1 \ \cdot s_1 \ - \ h_1 \ \cdot r_2 \quad \equiv \quad r_1 \ \cdot k_2 \ \cdot s_2 \ - \ h_1 \ \cdot r_1 \pmod{n}\] \[(r_2 \ \cdot k_1 \ \cdot s_1) \ \ - \ (r_1 \ \cdot k_2 \ \cdot s_2) \quad \equiv \quad h_1 \ \cdot r_2 \ - \ h_1 \ \cdot r_1 \pmod{n}\]This means that for some \( a \) where \( (a \in \mathbb{Z}^+) \) :
\[\quad \therefore (r_2 \ \cdot k_1 \ \cdot s_1) \ \ - \ (r_1 \ \cdot k_2 \ \cdot s_2) \quad + \quad a \ \cdot n \quad = \quad \quad h_1 \ \cdot r_2 \ - \ h_1 \ \cdot r_1\]Now substituting the mathematical expression that we derived for k in this challenge:
Matrices, Lattices, rkm0959’s CVP Inequality Solver and the Extended Hidden Number Problem
This is the part where the level of mathematics was far beyond us. We managed to solve the challenge by carefully looking at and observing how people solved the H1 challenge in Google CTF 2021. After obtaining the mathematical expression shown above, we used rkm0959’s Inequality Solver with CVP. We observed his writeup for the H1 challenge and created a similar matrix to the one he used for that challenge, only this time we would be using the mathematical expressions derived above.
Hence we constructed a 53 by 53 matrix such that :
\[\begin{bmatrix} 1 & 0 & 0 & 0 & \text{...} & 0 & 0 & 0 & r2 \ \cdot s1 \ \cdot 2^{8 \ \cdot 0} \pmod{n} \\ 0 & 1 & 0 & 0 & \text{...} & 0 & 0 & 0 & r2 \ \cdot s1 \ \cdot 2^{8 \ \cdot 1} \pmod{n} \\ 0 & 0 & 1 & 0 & \text{...} & 0 & 0 & 0 & r2 \ \cdot s1 \ \cdot 2^{8 \ \cdot 2} \pmod{n} \\ 0 & 0 & 0 & 1 & \text{...} & 0 & 0 & 0 & r2 \ \cdot s1 \ \cdot 2^{8 \ \cdot 3} \pmod{n} \\ \vdots & \vdots & \vdots & \vdots & \text{...} & \vdots & \vdots & \vdots & \vdots & \\ 0 & 0 & 0 & 0 & \text{...} & 1 & 0 & 0 & r1 \ \cdot s2 \ \cdot 2^{8 \ \cdot 49} \pmod{n} \\ 0 & 0 & 0 & 0 & \text{...} & 0 & 1 & 0 & r1 \ \cdot s2 \ \cdot 2^{8 \ \cdot 50} \pmod{n} \\ 0 & 0 & 0 & 0 & \text{...} & 0 & 0 & 1 & r1 \ \cdot s2 \ \cdot 2^{8 \ \cdot 51} \pmod{n} \\ 0 & 0 & 0 & 0 & \text{...} & 0 & 0 & 0 & n \\ \end{bmatrix}\]After creating this matrix, we made sure that the lower bound and upper bounds for the CVP solver were 48 and 57 respectively as each ‘byte’ (as defined above where a byte consists of the 3 as well as the unknown digit nibble from 0 to 9) would range from 48 + 0 all the way to 48 + 9. After taking some time to set up the matrix and fine tune it, we could then chuck it into the CVP solver and hopefully obtain all ‘bytes’ for each of the 2 nonces we are solving for. I hope to understand how the solver works in the future, all I am aware of is that it uses advanced lattice based reduction techniques like the Lenstra–Lenstra–Lovász lattice basis reduction algorithm , popularly known as LLL and solves the Extended Hidden Number Problem in order to recover the nonce.
Nearly always, the solver gave us the nonce ‘bytes’ (the 3 and unknown digit) from the LSB to the MSB. The incredibly egregious mistake that we made was that for some reason which we will never know, we were reading from the MSB to the LSB and never even detected this error. We knew something was going wrong obviously and we thought that somehow, somewhere the matrix that we setup was incorrect. Maybe because we were staying up late at around 4 am, we were just exhausted? Anyways, Diamondroxxx messages me 7 minutes after the CTF ended that he realized that we were reading from the MSB to the LSB. After that we really wanted to know if what we did was correct and indeed it was after fixing the error. Hence we could recover the nonce k and hence easily recover the private key d, after which signing any message was trivial.
After looking at the writeups, it turns out that most people were using another lattice reduction algorithm known as BKZ (Block Korkine Zolotarev) including rkm himself (he was also using his CVP Inequality solver). We also tried out the BKZ algorithm and althought it worked, for us, LLL was much faster.
The complete solve script can be found here :
from Crypto.Util.number import *
from pwn import *
from hashlib import sha256
from Crypto.Cipher import AES, PKCS1_OAEP, PKCS1_v1_5
from Crypto.PublicKey import RSA
from Crypto.Util.number import inverse, long_to_bytes, bytes_to_long, isPrime, getPrime, GCD
from tqdm import tqdm
from pwn import *
from sage.all import *
import itertools, sys, json, hashlib, os, math, time, base64, binascii, string, re, struct, datetime, subprocess
import numpy as np
import random as rand
import multiprocessing as mp
from base64 import b64encode, b64decode
from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives import padding
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
from sage.modules.free_module_integer import IntegerLattice
debug = False
r = remote("34.146.212.53", 35719, level = 'debug') if debug else remote("34.146.212.53", 35719)
def getParams():
r.sendlineafter('choice? ', '1')
r.recvuntil('x = ')
x = int(r.recvline())
r.recvuntil('s = ')
s = int(r.recvline())
return x, s
r1, s1 = getParams()
r2, s2 = getParams()
#r1, s1 = 25299575620856660513253162753471397988194505881018893682712853954194329703324, 36261785401375447770011298133226439363044520945863475872885710594694732329376
#r2, s2 = 80458902368259072038288476935794243607137540668215255671792235512580948732649, 53633268262377198291420595525986382238055587878314801412161803580794335400339
n = 115792089237316195423570985008687907852837564279074904382605163141518161494337
F = GF(n)
def shaa256(val):
h = hashlib.sha256()
h.update(val)
return bytes_to_long(h.digest())
h1 = shaa256(b'Baba')
def Babai_CVP(mat, target):
M = IntegerLattice(mat, lll_reduce=True).reduced_basis
G = M.gram_schmidt()[0]
diff = target
for i in reversed(range(G.nrows())):
diff -= M[i] * ((diff * G[i]) / (G[i] * G[i])).round()
return target - diff
def solve(mat, lb, ub, weight = None):
num_var = mat.nrows()
num_ineq = mat.ncols()
max_element = 0
for i in range(num_var):
for j in range(num_ineq):
max_element = max(max_element, abs(mat[i, j]))
if weight == None:
weight = num_ineq * max_element
# sanity checker
if len(lb) != num_ineq:
print("Fail: len(lb) != num_ineq")
return
if len(ub) != num_ineq:
print("Fail: len(ub) != num_ineq")
return
for i in range(num_ineq):
if lb[i] > ub[i]:
print("Fail: lb[i] > ub[i] at index", i)
return
# heuristic for number of solutions
DET = 0
if num_var == num_ineq:
DET = abs(mat.det())
num_sol = 1
for i in range(num_ineq):
num_sol *= (ub[i] - lb[i])
if DET == 0:
print("Zero Determinant")
else:
num_sol //= DET
# + 1 added in for the sake of not making it zero...
print("Expected Number of Solutions : ", num_sol + 1)
# scaling process begins
max_diff = max([ub[i] - lb[i] for i in range(num_ineq)])
applied_weights = []
for i in range(num_ineq):
ineq_weight = weight if lb[i] == ub[i] else max_diff // (ub[i] - lb[i])
applied_weights.append(ineq_weight)
for j in range(num_var):
mat[j, i] *= ineq_weight
lb[i] *= ineq_weight
ub[i] *= ineq_weight
# Solve CVP
target = vector([(lb[i] + ub[i]) // 2 for i in range(num_ineq)])
result = Babai_CVP(mat, target)
for i in range(num_ineq):
if (lb[i] <= result[i] <= ub[i]) == False:
print("Fail : inequality does not hold after solving")
break
# recover x
fin = None
if DET != 0:
mat = mat.transpose()
fin = mat.solve_right(result)
## recover your result
return result, applied_weights, fin
M = Matrix(ZZ, 53, 53)
lb = [0] * 53
ub = [0] * 53
for i in range(0, 26):
M[i, 52] = ( r2*s1*(1 << (8*i) ) ) % n
M[i+26, 52] = n - (r1*s2*(1 << (8*i) ) ) % n
M[52, 52] = n
lb[52] = (r2 * h1 - r1 * h1) % n
ub[52] = (r2 * h1 - r1 * h1) % n
for i in range(0, 52):
M[i, i] = 1
lb[i] = 48
ub[i] = 48+9
result, applied_weights, fin = solve(M, lb, ub, weight = 1)
fin = tuple(fin)
print(f"fin is {fin}")
try:
k1 = int(''.join(['3' + chr(i) for i in fin[:26][::-1]]), 16)
k2 = int(''.join(['3' + chr(i) for i in fin[51:25:-1]]), 16)
print(f"k1 is {hex(k1)}")
print(f"k2 is {hex(k2)}")
d1 = (s1 * k1 - h1) * inverse_mod(r1, n) % n
d2 = (s2 * k2 - h1) * inverse_mod(r2, n) % n
assert d1 == d2
except Exception as e:
print(e)
exit()
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
G = (0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
E = EllipticCurve(GF(p), [a, b])
G = E(G)
toSendH = shaa256(b'Flag')
k = 420
x, _ = (k*G).xy()
s = inverse_mod(k, n) * (toSendH + int(x) * d1) % n
r.sendlineafter('choice? ', '2')
r.sendlineafter('Which rule do you want to know? ', 'Flag')
r.sendlineafter('x? ', str(x))
r.sendlineafter('s? ', str(s))
print(r.recvline())
#b'Flag is TSGCTF{CRYPTO_IS_LOCK._KEY_IS_OPEN._CTF_IS_FUN!}\n'
Closing Thoughts
- Although I don’t understand enough about lattice reduction techniques, I am still glad that we were able to solve this challenge. This is something I want to spend time on and understand in the immediate future.
- The writeups for the H1 challenge in Google CTF 2021 is a gift that keeps on giving.
- rkm’s solver is one of humanity’s greatest treasures
- Technically, we only solved this challenge slightly after the CTF ended. Since we also failed to solve H1, hopefully we can solve the third biased nonce ECDSA challenge (third times the charm) as I dont want it to be L-L-L, pun intended ;D